Pravu liniju dobijenu međusobnim presjekom dviju ravni u potpunosti određuju dvije tačke od kojih svaka pripada objema ravnima. Dakle, prava linija K 1 K 2 (sl. 163), duž koje je ravan definisana trouglom ABC i pl. β, dat pravima DE i DF, prolazi kroz tačke K 1 i K 2; ali u tim tačkama prave AB i AC prve ravni sijeku kvadrat. β tj. tačke K 1 i K 2 pripadaju obe ravni.

dakle, u opštem slučaju, da biste konstruisali liniju preseka dve ravni, morate pronaći bilo koje dve tačke, od kojih svaka pripada obe ravni; ove tačke definišu liniju preseka ravnina.

Da biste pronašli svaku od ove dvije točke, obično je potrebno izvesti posebne konstrukcije. Ali ako je barem jedna od ravnina koje se sijeku okomita na ravninu projekcije, tada je konstrukcija projekcija linije ukrštanja pojednostavljena. Počnimo sa ovim slučajem.

Na sl. 164 prikazuje presek dve ravni, od kojih se jedna (definisana trouglom DEF) nalazi okomita na kvadrat. π 2. Kako je trokut DEF projektovan na kvadrat π 2 u obliku prave (D "F"), frontalna projekcija pravougaonog segmenta duž kojeg se sijeku oba trokuta je segment K " 1 K " 2 na projekciji D "F". Dalja konstrukcija je jasna iz crteža.

Drugi primjer je dat na sl. 165. Horizontalno projektovana ravan α seče ravan trougla ABC. Horizontalna projekcija linije presjeka ovih ravni - segmenta M"N" - određena je na tragu α".

Sada razmotrimo opšti slučaj konstruisanja linije preseka dve ravni. Neka je jedna od ravnina, β, definisana sa dve prave koje se seku, a druga, γ, sa dve paralelne prave. Konstrukcija je prikazana na sl. 166. Kao rezultat međusobnog presjeka ravnina β i γ, dobija se prava linija K 1 K 2. Izrazimo to tako što ćemo napisati: β × γ = K 1 K 2.

Za određivanje položaja tačaka K 1 i K 2 uzimamo dvije pomoćne frontalno projektovane ravni (α 1 i α 2) koje sijeku svaku od ravnina β i γ. Kada se ravni β i γ seku sa ravninom α 1. dobijamo prave linije sa projekcijama 1"2", 1"2" i 3"4", 3"4". Ove ravne linije, smještene u kvadratu. α 1 , na njihovom preseku odredite prvu tačku, K 1 , presečnu liniju ravni β i γ.

Dobivši projekcije K" 1 i K" 2, nalazimo na tragovima i α" 1 i α" 2 projekcije K" 1 i K" 2. Ovim se određuju projekcije K" 1 K" 2 i K" 1 K" 2 željene prave linije preseka ravnina β i γ (projekcije su nacrtane crtkanom linijom).

Pri konstruisanju treba imati na umu sledeće: pošto su pomoćne ravni sečenja α 1 i α 2 međusobno paralelne, onda, konstruišući projekcije 1"2" i 3"4", treba uzeti po jednu tačku za projekcije 5" 6" i 7"8" , najmanje 5 i 8, od 5"6"||1"2" i 7"8"||3"4".

U razmatranoj konstrukciji kao pomoćne su uzete dvije frontalno-projektirane ravni. Naravno, bilo je moguće uzeti i druge ravnine, na primjer, dvije horizontalne ili jednu horizontalnu, drugu frontalnu, itd. Suština konstrukcija se od toga ne mijenja. Međutim, takav slučaj se može dogoditi. Pretpostavimo da su dvije horizontalne ravni uzete kao pomoćne i one dobijene kada su se ukrštale

ispostavilo se da su β i γ horizontalne ravni međusobno paralelne. Ali pirinač. 167 pokazuje da se β i γ sijeku, iako su njihove horizontalne linije paralelne. Slijedom toga, nakon što smo dobili međusobno paralelne horizontalne projekcije horizontala AB i CD i znajući da ravnine nisu nužno paralelne, ali se mogu seći (duž za njih zajedničke horizontale), potrebno je testirati ravnine β i γ koristeći najmanje horizontalno projektovana ravan (vidi . sl. 167); ako bi se i prave linije duž kojih se ova pomoćna ravan σ seče β i γ ispostavile da su paralelne jedna s drugom, tada se ravni β i γ ne sijeku, već su paralelne jedna s drugom. Na sl. 167 ove prave se seku u tački K, kroz koju linija preseka ravni β i γ prolazi paralelno sa pravim BA i CD.

Ako su ravni definisane svojim tragovima na ravnima projekcije, onda je prirodno tražiti tačke koje definišu liniju preseka ravnina u tačkama preseka istih tragova ravni (Sl. 168): prava linija koja prolazi kroz ove tačke je zajednička za obje ravni, odnosno njihove linije ukrštanja.

Šema za konstruisanje linije preseka dve ravni (videti sliku 166) može se, naravno, proširiti i na slučaj zadavanja ravni njihovim tragovima. Ovdje ulogu pomoćnih reznih ravni igraju same projekcijske ravnine:

α × π 1 =h" 0α ; β× π 1 =h" 0β ; h" 0α × h" 0β =M;

α × π 2 =f" 0α ; β× π 2 =f" 0β ; f" 0α × f" 0β =N.

Točke sjecišta istoimenih ravninskih tragova su tragovi linije presjeka ovih ravni. Dakle, da bi se konstruisale projekcije linije preseka ravni α i β (slika 168), potrebno je: 1) pronaći tačku M" na preseku tragova h" 0α i h" 0β

i tačka N" na preseku f" 0α i f" 0β, a duž njih - projekcije M" i N"; 2) povući prave M"N" i M"N",

Na sl. 169-171 prikazuju slučajeve u kojima je poznat smjer raskrsnice. Dakle, dovoljno je imati samo jednu tačku od preseka tragova, a zatim povući pravu liniju kroz ovu tačku, na osnovu položaja ravni i njihovih tragova.

Pitanja za §§ 22-24

1. Koju relativnu poziciju mogu zauzeti dvije ravni?
2. Koji je znak paralelizma dvije ravni?
3. Kako su međusobno locirani frontalni tragovi dvije paralelne prednje projekcijske ravni?
4. Kako su međusobno locirani horizontalni tragovi dvije paralelne horizontalno projektovane ravni?
5. Kako se međusobno nalaze istoimene staze dvaju paralelnih aviona?
6. Da li je presek barem jednog para njihovih istoimenih koloseka znak međusobnog preseka dve ravni?
7. Kako odrediti relativni položaj prave i ravni?
8. Kako se konstruiše tačka preseka prave sa ravninom koja je okomita na jednu ili dve projekcijske ravni?
9. Koja tačka od onih koje se nalaze na zajedničkoj okomici na a) pl. π 1 b) pl. π 2 se smatra vidljivim na π 1, odnosno na π 2?
10. Kako konstruisati liniju presjeka dvije ravni, od kojih je barem jedna okomita na kvadrat. π 1 ili do pl. π 2?
11. Koja je opšta metoda za konstruisanje linije preseka dve ravni?

Na slici 1.3.25 prikazan je primjer konstruisanja linije presjeka dvije ravni metodom sečenja međuravni. Avion S određena linijama koje se seku A I b, i avion Q– paralelne linije With I d.

Da pronađem liniju l ravninske raskrsnice S I Q Nacrtajmo dvije frontalno projektovane ravni W(W 2) I W¢(W¢ 2), koji su posrednici. Avion W seče ove ravni S I Q u ravnim linijama 1-2 (1 2 -2 2 , 1 1 -2 1 ) I 3-4 (3 2 -4 2 , 3 1 -4 1 ). Označimo točku preseka ovih pravih sa TO(K 1, K 2). Dot TO pripada trima ravnima istovremeno S, Q, W. Dakle, poenta TO S I Q. Avion W¢ seče ravni S I Q u ravnim linijama 5-6 (5 1 -6 1 , 5 2 -6 2 ) I 7-8 (7 1 -8 1 , 7 2 -8 2 ). Tačka preseka ovih linija je tačka K¢. Ona je kao menstruacija TO pripada liniji presjeka ravnina S I Q. Stoga, pravo l, prolazeći kroz tačke TO I K¢, postoji željena prava linija preseka ovih ravni S I Q.

Slika 1.3.26 – Presek dve ravni u opštem položaju

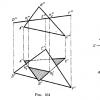
Na slici 1.3.26 prikazan je primjer konstruisanja linije preseka dve ravni presecanjem prave sa ravninom. Ravnine su definisane trouglovima ABC I EGF. Pomoćne rezne ravni S(S 2) I S¢(S 2) se povlače kroz strane Npr. I Ned trouglovi. Avion S(S 2) seče trougao ABC u pravoj liniji 1-2 . Dot TO Npr. I 1-2 . Avion S¢(S¢ 2) seče trougao EGF u pravoj liniji 3-4 . Dot K¢ je rezultat presjeka linija Ned I 3-4 . Poeni TO I K¢ ograničiti segment željene linije ukrštanja koja se nalazi unutar oba trougla.

Relativna vidljivost trouglova određena na frontalnom pogledu korištenjem konkurentskih tačaka 2 I 4 , od čega tačka 4 strane Npr. pokriva poentu 2 strane Ned. Vidljivost na horizontalnoj ravni projekcija određuje se korištenjem konkurentskih tačaka 5 I 6 , od čega tačka 6 strane Npr. pokriva poentu 5 strane AC.

Zakrivljene linije

Kriva linija se može smatrati tragom pokretne tačke. Ova tačka može biti jedna tačka ili tačka koja pripada liniji ili površini koja se kreće u prostoru.

Krive linije se mogu formirati presjekom krive površine s ravninom (u opštem slučaju), međusobnim presjekom dvije površine, od kojih je barem jedna kriva.

Zakon formiranja krive linije je skup uslova koji određuju ovu liniju. Tačka, linija, površina kreću se u prostoru, podložni različitim uslovima. Ravan može seći različite zakrivljene površine u različitim smjerovima. Veliki izbor površina može se ukrštati na različitim pozicijama jedna u odnosu na drugu. Iz toga slijedi da formiranje krive linije može biti podvrgnuto beskonačnom broju uslova i da se može formirati beskonačan broj zakrivljenih linija. Osim toga, ista zakrivljena linija može se formirati na različite načine.

Na primjer, elipsa se može formirati kretanjem tačke u ravni, u kojoj je u svakom trenutku zbroj udaljenosti od ove tačke do dvije druge fiksne tačke - žarišta elipse - konstantan i jednak velika osa elipse. Ali elipsa se može formirati i presjekom kružnog cilindra s ravninom koja se nalazi proizvoljno u odnosu na njegovu os ili potpunim presjekom površina dva kružna cilindra istog promjera.

Sve krive linije prema položaju njihovih tačaka u prostoru dijele se u dvije vrste: ravne krive– krive čije sve tačke leže u istoj ravni (na primjer, krug, elipsa, parabola, itd.) i prostorne krive– krive čije tačke ne leže u istoj ravni, na primjer, spirala

Prava linija u prostoru se može definisati kao linija preseka dve neparalelne ravni, odnosno kao skup tačaka koje zadovoljavaju sistem dve linearne jednačine

(V.5)

Obrnuta tvrdnja je takođe tačna: sistem dve nezavisne linearne jednačine oblika (V.5) definiše pravu liniju kao liniju preseka ravni (ako nisu paralelne). Jednačine sistema (V.5) se nazivaju opšta jednačina prava linija u prostoru
.

PrimjerV.12 . Sastaviti kanonsku jednačinu prave date općim jednačinama ravnina

Rješenje. Da biste napisali kanonsku jednačinu prave ili, što je ista stvar, jednačinu prave koja prolazi kroz dvije date tačke, morate pronaći koordinate bilo koje dvije tačke na pravoj. One mogu biti tačke preseka prave linije sa bilo koje dve koordinatne ravni, na primer Oyz I Oxz.

Tačka preseka prave i ravni Oyz ima apscisu
. Stoga, pretpostavljajući u ovom sistemu jednačina
, dobijamo sistem sa dve varijable:

Njena odluka
,
zajedno sa
definiše tačku
željenu pravu liniju. Uz pretpostavku u ovom sistemu jednačina
, dobijamo sistem

čije rešenje
,
zajedno sa
definiše tačku
presek prave sa ravninom Oxz.

Zapišimo sada jednačine prave koja prolazi kroz tačke
I
:
ili
, Gdje
će biti vektor smjera ove prave linije.

PrimjerV.13. Prava linija je data kanonskom jednadžbom
. Napišite opštu jednačinu za ovu liniju.

Rješenje. Kanonska jednačina prave linije može se napisati kao sistem dvije nezavisne jednačine:



Dobili smo opštu jednačinu prave, koja je sada data presekom dve ravni, od kojih je jedna
paralelno sa osom Oz (
), i drugi
– sjekire Oh (
).

Ova prava linija se može predstaviti kao linija presjeka dvije druge ravni pisanjem njene kanonske jednadžbe u obliku drugog para nezavisnih jednačina:



Komentar . Ista prava linija se može definisati različitim sistemima dveju linearnih jednačina (odnosno presekom različitih ravni, pošto se kroz jednu pravu liniju može povući beskonačan broj ravni), kao i različitim kanonskim jednačinama (u zavisnosti od izbor tačke na pravoj liniji i njenog vektora pravca) .

Nazvat ćemo ga vektor različit od nule paralelan pravoj liniji vodeći vektor .

Pustiti u trodimenzionalni prostor data je ravna linija l, prolazeći kroz tačku
, i njegov vektor smjera
.

Bilo koji vektor
, Gdje
, koja leži na pravoj, kolinearna je s vektorom , stoga su njihove koordinate proporcionalne, tj

.

(V.6)

Ova jednačina se zove kanonska jednačina prave. U posebnom slučaju kada je ﻉ ravan, dobijamo jednačinu prave linije na ravni

PrimjerV.14. .
,
.

,

(V.7)
,
,
.

Naći jednačinu prave koja prolazi kroz dvije tačke

,

(V.7) Gdje Pogodno je zapisati jednačinu (V.6) u parametarskom obliku. Pošto su koordinate vektora pravca paralelnih linija proporcionalne, onda, pod pretpostavkom
.

t

- parametar,
Udaljenost od tačke do linije l Razmotrimo dvodimenzionalni euklidski prostor ﻉ sa Dekartovim koordinatnim sistemom. Pusti poentu
ﻉ i lﻉ. Nađimo udaljenost od ove tačke do prave. Hajde da stavimo
, i ravno

dato jednačinom
(Sl.V.8).
Udaljenost
, vektor l,
, Gdje – vektor normalne linije
I
,
.

– kolinearne, pa su im koordinate proporcionalne, tj
, dakle, Odavde I ili množenjem ovih jednačina sa A
B

.

odnosno, i zbrajajući ih nalazimo

, odavde
(V.8)
.

PrimjerV.15. određuje udaljenost od tačke
na pravu liniju l:
Naći jednačinu prave koja prolazi kroz tačku
(V.8) l.

okomito na pravu liniju
i pronađite udaljenost od l
Od sl. V.8 imamo

, a vektor normale je ravan
. Iz uslova okomitosti imamo

Jer

, To
.
.

(V.9)
Ovo je jednadžba prave koja prolazi kroz tačku l:
, okomito na pravu liniju
(V.8) l Neka nam je jednačina prave (V.9) koja prolazi kroz tačku

, okomito na pravu
. Pronađite udaljenost od tačke
, koristeći formulu (V.8).
Da biste pronašli traženu udaljenost, dovoljno je pronaći jednadžbu prave linije koja prolazi kroz dvije tačke

, a vektor normale je ravan
i tačka
. Iz uslova okomitosti imamo

leži na liniji u osnovi okomice. Neka

, Onda
, i vektor l.
ili

(V.11)

Od tačke

,

leži na pravoj liniji

, onda imamo još jednu jednakost

PrimjerV.16. Hajde da svedemo sistem na oblik pogodan za primenu Cramerove metode
Njegovo rješenje ima oblik
.
(V.12)
Zamjenom (V.12) u (V.10) dobijamo originalnu udaljenost.
na osnovu okomice na prvobitnu liniju.

Po formuli (V.8) imamo

Pronalazimo jednadžbu prave koja sadrži okomicu kao prava koja prolazi kroz dvije tačke
I
, koristeći formulu (V.11). Jer
, zatim, uzimajući u obzir činjenicu da
, A
, imamo

.

Da pronađem koordinate
imamo sistem koji uzima u obzir činjenicu da je tačka
leži na originalnoj liniji

dakle,
,
, odavde.

Razmotrimo trodimenzionalni euklidski prostor ﻉ. Pusti poentu
ﻉ i avion ﻉ. Nađimo udaljenost od ove tačke
na ravan datu jednačinom (slika V.9).

Analogno dvodimenzionalnom prostoru imamo
i vektor
, ah, odavde

.

(V.13)
I
Jednačinu prave koja sadrži okomicu na ravan  zapisujemo kao jednadžbu prave koja prolazi kroz dvije tačke

, leži u avionu:

.
(V.14)

Da pronađemo koordinate tačke ,,bilo koje dvije jednakosti formule (V.14) dodajemo jednačinu
Rješavajući sistem od tri jednačine (V.14), (V.15), nalazimo

.

– koordinate tačke
. Tada će jednačina okomice biti zapisana u obliku

Za pronalaženje udaljenosti od tačke

na ravan umjesto formule (V.13) koju koristimo

Pravu liniju preseka dve ravni određuju dve tačke, od kojih svaka pripada obema ravnima, ili jedna tačka koja pripada dvema ravnima, i poznati pravac te prave. U oba slučaja, zadatak je pronaći tačku zajedničku za dvije ravni. Opšta tehnika za konstruisanje linije preseka dve ravni je sledeća. Uvodi se pomoćna ravan, konstruišu se linije preseka pomoćne ravni sa dve date, a na preseku konstruisanih pravih nalazi se zajednička tačka dve ravni. Da bi se pronašla druga zajednička tačka, konstrukcija se ponavlja pomoću druge pomoćne ravni. Slika 5 prikazuje vizuelni prikaz linije ukrštanja K 1 K 2 I Q.

dva aviona

R K 1 K 2 I Q Slika 5 S Za vizuelni prikaz konstrukcije prve zajedničke tačke linije preseka ravnina K 1 K 2(Slika 6) uvedena je pomoćna ravan 1-2 . Sa avionom Q seče duž linije 3-4 , sa avionom 1-2 I 3-4 – duž linije . Na raskrsnici linija određena prva zajednička tačka K 1 K 2 K 1 dva aviona I

Q

– prva tačka linije njihovog preseka.

Slično, uvodi se nova rezna ravan i konstruiše se druga tačka presečne linije.

Kao primjer, na slici 7 prikazana je konstrukcija projekcija m"n", mn raskrsnice MN ravan frontalne projekcije K 1 K 2 sa ravninom trougla ABC.

Slika 7

Na frontalnoj projekciji na sjecištu projekcija a"b" I a"c" sa tragom P u pronađite frontalne projekcije m" I n" dve zajedničke tačke datih ravni. Na osnovu njih su konstruisane horizontalne projekcije m I n na horizontalnim projekcijama ab K 1 ac strane trougla. Kroz tačke m I n Crtamo horizontalnu projekciju linije presjeka ravnina. Gledajući duž strelice S iz frontalne projekcije vidljivo je da je dio trougla lijevo od presječne linije MN(m"n") je iznad ravni K 1 K 2, tj. vidljivo, ostalo je ispod aviona R, tj. nevidljiv (odjeljak mbcn prikazano isprekidanom linijom).

Još jedan primjer konstruiranja linije presjeka dvije trokutne ploče ABC I DEF, od kojih jedan ( DEF) je specificirana kao horizontalno projektovana ravan, prikazana na slici 8.

Slika 8

Na horizontalnoj projekciji na sjecištu horizontalnih projekcija ab I bc stranke DABC sa projekcijom dfe drugog trokuta nalazimo horizontalne projekcije m I n tačke njihovog preseka. Prema njima na frontalnim projekcijama strana a"b" I b"c" konstruisanje frontalnih projekcija m" I n" raskrsnice MN. Na frontalnoj projekciji bilježimo vidljivost dijelova trokuta, vođeni sljedećim: kada se gleda duž strelice S iz horizontalne projekcije je očigledno da je strana AC je ispred ravni trougla DEF.

Dakle, strana AC i njome ograničen dio trougla ABC do raskrsnice MN vidljiva (tj. vidljiva je frontalna projekcija četvorougla a"c"n"m"). Vidljivi dio frontalne projekcije DDEF osenčeno na crtežu.

Konstrukcija linije preseka ravni u opštem položaju. Na slici 9 prikazana je konstrukcija projekcija m"n", mn linije preseka dve ravni, od kojih je jedna definisana projekcijama a"b", b"c", ab, bc dvije linije koje se seku, druga - projekcije d"e", f"g", de, fg dve paralelne prave.

Dvije horizontalne ravni, definirane tragovima, uzimaju se kao pomoćne ravni R u I T u .

Avion R seče prvu datu ravan u pravoj liniji 1-2 , drugi - u pravoj liniji 3-4 . Prema frontalnim projekcijama 1", 2" I 3", 4" nalazimo horizontalne projekcije pomoću komunikacijskih linija 1, 2 I 3, 4 na horizontalnim projekcijama ab, bc, de, fg ravno Kroz njih crtamo horizontalne projekcije linija 1-2 I 3-4 raskrsnice. Označite tačku m– horizontalna projekcija zajedničke tačke M tri ravni - dva data i pomoćna R. Pomoću njega određujemo frontalnu projekciju m" na frontalnoj stazi R u pomoćni avion.

Slika 9

Pomoćni avioni T I R paralelno. Prave njihovog preseka sa datim ravnima su takođe paralelne. Dakle, horizontalne projekcije linija presjeka ravnine T sa datim ravnima se povlače kroz projekciju b paralelno sa projekcijom 1-2 i kroz projekciju 5 paralelno sa projekcijom 3-4 . Na njihovoj raskrsnici pronađena je horizontalna projekcija n druga zajednička tačka tri ravni, tj. linije preseka dve date ravni. Uz njega na frontalnoj stazi T u frontalna projekcija je konstruisana na pomoćnoj ravni n". Kroz izgrađene projekcije m",n" I m, n Izvodimo frontalne i horizontalne projekcije željene linije raskrsnice MN.

Dvije ravni se sijeku jedna drugu u pravoj liniji. Da bismo ga konstruisali, potrebno je odrediti dve tačke koje istovremeno pripadaju svakoj od datih ravni. Pogledajmo kako se to radi koristeći sljedeće primjere.

Nađimo liniju presjeka generičkih ravni α i β za slučaj kada je pl. α je dato projekcijama trougla ABC, a pl. β – paralelne prave d i e. Rješenje ovog problema izvodi se konstruisanjem tačaka L 1 i L 2 koje pripadaju liniji ukrštanja.

Rješenje

1. Uvodimo pomoćnu horizontalnu ravan γ 1. Seče α i β duž pravih linija. Frontalne projekcije ovih linija, 1""C"" i 2""3"", poklapaju se sa frontalnim tragom kvadrata. γ 1. Na slici je označen kao f 0 γ 1 i nalazi se paralelno sa x osom.
2. Određujemo horizontalne projekcije 1"C" i 2"3" duž komunikacijskih linija.
3. Horizontalnu projekciju tačke L 1 nalazimo na presjeku pravih 1 "C" i 2 "3". Frontalna projekcija tačke L 1 leži na frontalnom tragu ravnine γ.
4. Uvodimo pomoćnu horizontalnu ravan γ 2. Koristeći konstrukcije slične onima opisanim u paragrafima 1, 2, 3, nalazimo projekcije tačke L 2.
5. Kroz L 1 i L 2 povlačimo željenu pravu liniju l.

Vrijedi napomenuti da kao pl. γ pogodno je koristiti i ravni ravni i ravni projekcije.

Nađimo liniju preseka ravni α i β, definisanu tragovima. Ovaj zadatak je mnogo jednostavniji od prethodnog. Ne zahtijeva uvođenje pomoćnih aviona. Njihovu ulogu igraju ravni projekcije P 1 i P 2.

Algoritam izgradnje

1. Nalazimo tačku L" 1, koja se nalazi na preseku horizontalnih tragova h 0 α i h 0 β. Tačka L"" 1 leži na x-osi. Njen položaj se određuje pomoću linije veze povučene iz L" 1.
2. Nalazimo tačku L"" 2 na sjecištu frontalnih tragova pl. α i β. Tačka L" 2 leži na x osi. Njen položaj je određen duž linije veze povučene iz L"" 2.
3. Povlačimo prave l" i l"" kroz odgovarajuće projekcije tačaka L 1 i L 2, kao što je prikazano na slici.

Dakle, prava linija l koja prolazi kroz tačke preseka tragova ravni je željena.

Presjek ravni trouglova

Razmotrimo konstruisanje linije preseka ravni definisanih trouglovima ABC i DEF i određivanje njihove vidljivosti metodom konkurentskih tačaka.

Algoritam izgradnje

1. Kroz pravu DE povlačimo frontalno projektovanu ravan σ: njen trag f 0σ je naznačen na crtežu. Ravan σ seče trougao ABC duž prave 35. Označivši tačke 3""=A""B""∩f 0σ i 5""=A""S""∩f 0σ, odredimo položaj (∙ )3" i (∙) 5" duž komunikacijskih linija na ΔA"B"C".
2. Nalazimo horizontalnu projekciju N"=D"E"∩3"5" tačke N preseka pravih DE i 35, koje leže u pomoćnoj ravni σ. Projekcija N"" nalazi se na frontalnom tragu f 0σ na istoj liniji veze sa N".

Kroz pravu BC povlačimo frontalno projektovanu ravan τ: njen trag f 0τ je naznačen na crtežu. Koristeći konstrukcije slične onima opisanim u paragrafima 1 i 2 algoritma, nalazimo projekcije tačke K.

3. Kroz N i K povlačimo željenu pravu liniju NK - liniju preseka ΔABC i ΔDEF.

Definicija vidljivosti

Frontalno konkurentne tačke 4 i 5, koje pripadaju ΔDEF i ΔABC, respektivno, nalaze se na istoj frontalno izbačenoj liniji, ali se nalaze na različitim udaljenostima od ravni projekcije π 2. Pošto je (∙)5" bliži posmatraču od (∙)4", u projekciji na kvadrat je vidljiv odeljak ΔABC sa svojim (∙)5. π 2. Na suprotnoj strani linije N""K"" vidljivost trouglova se mijenja.

Horizontalno konkurentne tačke 6 i 7, koje pripadaju ΔABC i ΔDEF, respektivno, nalaze se na istoj horizontalno projektovanoj pravoj liniji, ali se nalaze na različitim udaljenostima od ravni projekcije π 1 . Pošto se (∙)6"" nalazi više od (∙)7"", onda je u projekciji na kvadrat vidljiv odeljak ΔABC sa svojim (∙)6. π 1. Na suprotnoj strani N"K" linije vidljivost trouglova se mijenja.