Taisni, kas iegūta, savstarpēji krustojot divas plaknes, pilnībā nosaka divi punkti, no kuriem katrs pieder abām plaknēm. Tādējādi taisne K 1 K 2 (163. att.), pa kuru plakne, ko nosaka trīsstūris ABC un pl. β, kas dots ar taisnēm DE un DF, iet caur punktiem K 1 un K 2; bet šajos punktos pirmās plaknes taisnes AB un AC krustojas ar kvadrātu. β t.i. punkti K 1 un K 2 pieder abām plaknēm.

Tāpēc vispārīgā gadījumā, lai izveidotu divu plakņu krustošanās līniju, ir jāatrod jebkuri divi punkti, no kuriem katrs pieder abām plaknēm; šie punkti nosaka plakņu krustošanās līniju.

Lai atrastu katru no šiem diviem punktiem, parasti ir nepieciešams veikt īpašas konstrukcijas. Bet, ja vismaz viena no krustojošām plaknēm ir perpendikulāra projekcijas plaknei, tad krustojuma līnijas projekciju konstruēšana tiek vienkāršota. Sāksim ar šo gadījumu.

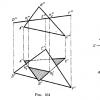
Attēlā 164 parāda divu plakņu krustpunktu, no kurām viena (noteikta ar trīsstūri DEF) atrodas perpendikulāri kvadrātam. π 2. Tā kā trijstūris DEF tiek projicēts uz kvadrāta π 2 taisnas līnijas veidā (D "F"), tad taisnes segmenta frontālā projekcija, pa kuru krustojas abi trijstūri, projekcijā ir segments K " 1 K " 2 D "F". Tālākā konstrukcija ir skaidra no zīmējuma.

Cits piemērs ir parādīts attēlā. 165. Horizontāli izvirzītā plakne α šķērso trijstūra ABC plakni. Šo plakņu krustošanās līnijas horizontālā projekcija - segments M"N" - tiek noteikta uz trases α".

Tagad apsvērsim vispārīgs divu plakņu krustošanās līnijas konstruēšanas gadījums. Viena no plaknēm β ir noteikta ar divām krustojošām taisnēm, bet otra, γ, ar divām paralēlām taisnēm. Konstrukcija ir parādīta attēlā. 166. Plakņu β un γ savstarpējās krustošanās rezultātā tiek iegūta taisne K 1 K 2. Izteiksim to, rakstot: β × γ = K 1 K 2.

Punktu K 1 un K 2 novietojuma noteikšanai ņemam divas frontāli izvirzītas palīgplaknes (α 1 un α 2), kas krusto katru no plaknēm β un γ. Kad plaknes β un γ krustojas ar plakni α 1. iegūstam taisnas līnijas ar projekcijām 1"2", 1"2" un 3"4", 3"4". Šīs taisnās līnijas, kas atrodas laukumā. α 1, to krustpunktā nosaka pirmo punktu K 1, plakņu β un γ krustošanās līniju.

Iegūstot projekcijas K" 1 un K" 2, uz trasēm α" 1 un α" 2 atrodam projekcijas K" 1 un K" 2. Tas nosaka vēlamās plakņu β un γ krustošanās taisnes projekcijas K" 1 K" 2 un K" 1 K" 2 (projekcijas zīmē ar punktu līniju).

Konstruējot var paturēt prātā sekojošo: tā kā griešanas palīgplaknes α 1 un α 2 ir savstarpēji paralēlas, tad, izveidojot projekcijas 1"2" un 3"4, projekcijām 5" jāņem pa vienam punktam. 6" un 7"8" , vismaz 5 un 8, jo 5"6"||1"2" un 7"8"||3"4".

Aplūkotajā konstrukcijā kā palīgierīces tika izmantotas divas frontāli izvirzītas lidmašīnas. Protams, varēja ņemt arī citas plaknes, piemēram, divas horizontālas vai viena horizontāla, otra frontāla utt. Konstrukciju būtība no tā nemainās. Tomēr šāds gadījums var notikt. Pieņemsim, ka divas horizontālās plaknes tika ņemtas par palīgierīcēm un tās, kas iegūtas, kad tās krustojas

horizontālās plaknes β un γ izrādījās savstarpēji paralēlas. Bet rīsi. 167 parāda, ka β un γ krustojas viens ar otru, lai gan to horizontālās līnijas ir paralēlas. Līdz ar to, saņemot horizontālu AB un CD savstarpēji paralēlas horizontālās projekcijas un zinot, ka plaknes ne vienmēr ir paralēlas, bet var krustoties (gar tām kopīgu horizontālu), ir jāpārbauda plaknes β un γ, izmantojot vismaz horizontāli izvirzīta plakne (sk. 167. att.); ja taisnes, pa kurām šī palīgplakne σ krusto β un γ, arī izrādītos paralēlas viena otrai, tad plaknes β un γ nekrustojas, bet ir paralēlas viena otrai. Attēlā 167 šīs taisnes krustojas punktā K, caur kuru plakņu β un γ krustošanās līnija iet paralēli taisnēm BA un CD.

Ja plaknes nosaka to pēdas uz projekcijas plaknēm, tad dabiski ir meklēt punktus, kas nosaka plakņu krustošanās līniju vienādu plakņu pēdu krustpunktos (168. att.): taisne, kas iet caur šiem punktiem, ir kopīga abām plaknēm, t.i., to līniju krustpunktiem.

Shēmu divu plakņu krustošanās līnijas konstruēšanai (sk. 166. att.), protams, var attiecināt arī uz gadījumu, kad plaknes tiek norādītas pēc to pēdām. Šeit papildu griešanas plakņu lomu spēlē pašas projekcijas plaknes:

α × π 1 = h" 0α ; β × π 1 = h" 0β ; h" 0α × h" 0β = M;

α × π 2 =f" 0α ; β × π 2 =f" 0β ; f" 0α × f" 0β =N.

Tāda paša nosaukuma plakņu pēdu krustošanās punkti ir šo plakņu krustošanās līnijas pēdas. Tāpēc, lai izveidotu plakņu α un β krustošanās līnijas projekcijas (168. att.), nepieciešams: 1) atrast punktu M" pēdu h" 0α un h" 0β krustpunktā.

un punktu N" f" 0α un f" 0β krustpunktā, un pa tām - projekcijas M" un N"; 2) novelciet taisnes M"N" un M"N",

Attēlā 169-171 parāda gadījumus, kad ir zināms krustojuma līnijas virziens. Tāpēc pietiek tikai ar vienu punktu no trašu krustpunkta un pēc tam caur šo punktu novilkt taisnu līniju, pamatojoties uz plakņu un to pēdu novietojumu.

Jautājumi 22.-24.§

1. Kādu relatīvo stāvokli var ieņemt abas plaknes?
2. Kāda ir divu plakņu paralēlisma zīme?
3. Kā savstarpēji atrodas divu paralēlu priekšpuses izvirzīto plakņu frontālās pēdas?
4. Kā savstarpēji atrodas divu paralēli horizontāli izvirzītu plakņu horizontālās pēdas?
5. Kā viena otrai paralēlas divu plakņu viena nosaukuma sliedes atrodas savstarpēji?
6. Vai vismaz viena tāda paša nosaukuma sliežu ceļu krustošanās ir divu plakņu savstarpēja krustošanās zīme?
7. Kā noteikt taisnas līnijas un plaknes relatīvo stāvokli?
8. Kā tiek konstruēts taisnes krustpunkts ar plakni, kas ir perpendikulāra vienai vai divām projekcijas plaknēm?
9. Kurš punkts no tiem, kas atrodas uz kopējā perpendikulāra a) pl. π 1 b) pl. π 2 tiek uzskatīts par redzamu attiecīgi uz π 1, uz π 2?
10. Kā izveidot krustošanās līniju divām plaknēm, no kurām vismaz viena ir perpendikulāra kvadrātam. π 1 vai līdz pl. π 2?
11. Kāda ir vispārējā metode divu plakņu krustošanās līnijas konstruēšanai?

Piemērs divu plakņu krustošanās līnijas konstruēšanai, izmantojot starpplakņu griešanas metodi, ir parādīts 1.3.25. attēlā. Lidmašīna S ko nosaka krustojošās līnijas A Un b, un lidmašīna J- paralēlas līnijas Ar Un d.

Lai atrastu līniju l plakņu krustojumi S Un J Uzzīmēsim divas frontāli izvirzītas plaknes W(W 2) Un W¢(W¢ 2), kas ir starpnieki. Lidmašīna W krusto šīs plaknes S Un J taisnās līnijās 1-2 (1 2 -2 2 , 1 1 -2 1 ) Un 3-4 (3 2 -4 2 , 3 1 -4 1 ). Apzīmēsim šo līniju krustošanās punktu ar UZ(K 1, K 2). Punkts UZ pieder pie trim plaknēm vienlaicīgi S, Q, W. Tāpēc punkts UZ S Un J. Lidmašīna W¢ krusto plaknes S Un J taisnās līnijās 5-6 (5 1 -6 1 , 5 2 -6 2 ) Un 7-8 (7 1 -8 1 , 7 2 -8 2 ). Šo līniju krustošanās punkts ir punkts K¢. Viņa ir kā periods UZ pieder pie plakņu krustošanās līnijas S Un J. Tāpēc taisni l, kas iet caur punktiem UZ Un K¢, ir vēlamā šo plakņu krustošanās taisne S Un J.

1.3.26. attēls. Divu plakņu krustpunkts vispārējā stāvoklī

1.3.26. attēlā parādīts piemērs divu plakņu krustošanās līnijas konstruēšanai, krustojot taisni ar plakni. Plaknes nosaka trīsstūri ABC Un EGF. Papildu griešanas plaknes S(S 2) Un S¢(S 2) ir izvilkti caur sāniem E.G. Un Sv trijstūri. Lidmašīna S(S 2) šķērso trīsstūri ABC taisnā līnijā 1-2 . Punkts UZ E.G. Un 1-2 . Lidmašīna S¢(S¢ 2) šķērso trīsstūri EGF taisnā līnijā 3-4 . Punkts K¢ ir līniju krustošanās rezultāts Sv Un 3-4 . Punkti UZ Un K¢ ierobežo vajadzīgās krustojuma līnijas segmentu, kas atrodas abos trīsstūros.

Trīsstūru relatīvā redzamība, kas noteikta frontālajā skatā, izmantojot konkurējošus punktus 2 Un 4 , no kura punkta 4 puses E.G. aptver būtību 2 puses Sv. Redzamību projekciju horizontālajā plaknē nosaka, izmantojot konkurējošus punktus 5 Un 6 , no kura punkta 6 puses E.G. aptver būtību 5 puses AC.

Izliektas līnijas

Izliektu līniju var uzskatīt par kustīga punkta pēdu. Šis punkts var būt viens punkts vai punkts, kas pieder līnijai vai virsmai, kas kustas telpā.

Izliektas līnijas var veidot, izliektas virsmas krustojoties ar plakni (vispārējā gadījumā), savstarpēji krustojot divas virsmas, no kurām vismaz viena ir līkne.

Izliektas līnijas veidošanās likums ir nosacījumu kopums, kas nosaka šo līniju. Punkts, līnija, virsma pārvietojas telpā, pakļaujoties dažādiem apstākļiem. Plakne var krustot dažādas izliektas virsmas dažādos virzienos. Dažādas virsmas var krustoties viena ar otru dažādās pozīcijās attiecībā pret otru. No tā izriet, ka izliektas līnijas veidošanos var pakļaut bezgalīgi daudziem nosacījumiem un var izveidot bezgalīgu skaitu izliektu līniju. Turklāt vienu un to pašu izliektu līniju var veidot dažādos veidos.

Piemēram, elipsi var izveidot, pārvietojoties kādam punktam plaknē, kurā jebkurā brīdī attālumu summa no šī punkta līdz diviem citiem fiksētiem punktiem - elipses fokusiem - ir nemainīga un vienāda ar elipses galvenā ass. Bet elipsi var izveidot arī, krustojoties apļveida cilindram ar plakni, kas patvaļīgi atrodas attiecībā pret tā asi, vai pilnībā krustojot divu vienāda diametra apļveida cilindru virsmas.

Visas izliektās līnijas atbilstoši to punktu novietojumam telpā ir sadalītas divos veidos: plakanas līknes– līknes, kuru visi punkti atrodas vienā plaknē (piemēram, aplis, elipse, parabola utt.) un telpiskās līknes– līknes, kuru punkti neatrodas vienā plaknē, piemēram, spirāle

Taisni telpā var definēt kā divu neparalēlu plakņu krustošanās līniju, tas ir, kā punktu kopu, kas atbilst divu lineāru vienādojumu sistēmai.

(V.5)

Patiess ir arī apgrieztais apgalvojums: divu neatkarīgu lineāru vienādojumu sistēma ar formu (V.5) definē taisni kā plakņu krustošanās līniju (ja tās nav paralēlas). Sistēmas (V.5) vienādojumus sauc vispārējais vienādojums taisna līnija telpā
.

PiemērsV.12 . Sastādiet taisnas līnijas kanonisku vienādojumu, ko nosaka plakņu vispārīgie vienādojumi

Risinājums. Lai uzrakstītu taisnes kanonisko vienādojumu vai, kas ir tas pats, vienādojumu tai līnijai, kas iet cauri diviem dotiem punktiem, jāatrod jebkuru divu taisnes punktu koordinātas. Tie var būt, piemēram, taisnas līnijas krustošanās punkti ar jebkurām divām koordinātu plaknēm Oyz Un Oxz.

Taisnes un plaknes krustpunkts Oyz ir abscisa
. Tāpēc, pieņemot, ka šajā vienādojumu sistēmā
, mēs iegūstam sistēmu ar diviem mainīgajiem:

Viņas lēmums
,
kopā ar
definē punktu
vēlamo taisno līniju. Pieņemot, ka šajā vienādojumu sistēmā
, mēs saņemam sistēmu

kura risinājums
,
kopā ar
definē punktu
taisnes krustojums ar plakni Oxz.

Tagad pierakstīsim līnijas vienādojumus, kas iet caur punktiem
Un
:
vai
, Kur
būs šīs taisnes virziena vektors.

PiemērsV.13. Taisni nosaka kanoniskais vienādojums
. Uzrakstiet šai līnijai vispārīgu vienādojumu.

Risinājums. Līnijas kanonisko vienādojumu var uzrakstīt kā divu neatkarīgu vienādojumu sistēmu:



Mēs esam ieguvuši vispārīgo taisnes vienādojumu, ko tagad dod divu plakņu krustpunkts, no kuriem viena
paralēli asij Oz (
), un otru
– cirvji Ak (
).

Šo taisni var attēlot kā divu citu plakņu krustošanās līniju, ierakstot tās kanonisko vienādojumu cita neatkarīgu vienādojumu pāra formā:



komentēt . Vienu un to pašu taisni var definēt ar dažādām divu lineāro vienādojumu sistēmām (tas ir, ar dažādu plakņu krustojumu, jo caur vienu taisni var novilkt bezgalīgu skaitu plakņu), kā arī ar dažādiem kanoniskiem vienādojumiem (atkarībā no taisnes punkta izvēle un tā virziena vektors) .

Nenulles vektors, kas ir paralēls taisnei, mēs to sauksim virzošais vektors .

Ielaidiet trīsdimensiju telpu ir dota taisna līnija l, kas iet caur punktu
, un tā virziena vektoru
.

Jebkurš vektors
, Kur
, kas atrodas uz līnijas, ir kolineārs ar vektoru , tāpēc to koordinātas ir proporcionālas, tas ir

.

(V.6)

Šo vienādojumu sauc par taisnes kanonisko vienādojumu. Īpašā gadījumā, kad ﻉ ir plakne, iegūstam plaknes taisnes vienādojumu

PiemērsV.14. .
,
.

,

(V.7)
,
,
.

Atrodiet vienādojumu taisnei, kas iet caur diviem punktiem

,

(V.7) Kur Vienādojumu (V.6) ir ērti rakstīt parametriskā formā. Tā kā paralēlo taisnu virziena vektoru koordinātas ir proporcionālas, tad, pieņemot
.

t

- parametrs,
Attālums no punkta līdz līnijai l Apsveriet divdimensiju Eiklīda telpu ﻉ ar Dekarta koordinātu sistēmu. Ļaujiet punktu
ﻉ un lﻉ. Noskaidrosim attālumu no šī punkta līdz līnijai. Liekam
, un taisni

ko dod vienādojums
(V.8. att.).
Attālums
, vektors l,
, Kur – parastās līnijas vektors
Un
,
.

– kolineāri, tātad to koordinātas ir proporcionālas, tas ir
, tātad, No šejienes Un vai reizinot šos vienādojumus ar A
B

.

attiecīgi un pievienojot tos, mēs atrodam

, no šejienes
(V.8)
.

PiemērsV.15. nosaka attālumu no punkta
uz taisnu līniju l:
Atrodiet vienādojumu taisnei, kas iet caur punktu
(V.8) l.

perpendikulāri taisnai līnijai
un atrodiet attālumu no l
No att. V.8 mums ir

, un parastais vektors ir taisns
. No perpendikularitātes nosacījuma, kas mums ir

Jo

, Tas
.
.

(V.9)
Šis ir līnijas vienādojums, kas iet caur punktu l:
,perpendikulāri taisnei
(V.8) l Pieņemsim taisnes (V.9) vienādojumu, kas iet caur punktu

, perpendikulāri līnijai
. Atrodiet attālumu no punkta
, izmantojot formulu (V.8).
Lai atrastu vajadzīgo attālumu, pietiek atrast taisnes vienādojumu, kas iet caur diviem punktiem

, un parastais vektors ir taisns
un periods
. No perpendikularitātes nosacījuma, kas mums ir

guļus uz līnijas perpendikula pamatnē. Ļaujiet

, Tad
, un vektoru l.
vai

(V.11)

Kopš punkta

,

atrodas uz taisnas līnijas

, tad mums ir vēl viena vienlīdzība

PiemērsV.16. Reducēsim sistēmu līdz tādai formai, kas ir ērta Krāmera metodes pielietošanai
Tā risinājumam ir forma
.
(V.12)
Aizvietojot (V.12) ar (V.10), iegūstam sākotnējo attālumu.
līdz perpendikula pamatnei sākotnējai līnijai.

Pēc formulas (V.8) mums ir

Mēs atrodam taisnes vienādojumu, kurā ir perpendikuls, kā taisni, kas iet caur diviem punktiem
Un
, izmantojot formulu (V.11). Jo
, tad, ņemot vērā faktu, ka
, A
, mums ir

.

Lai atrastu koordinātas
mums ir sistēma, ņemot vērā to, ka punkts
atrodas uz sākotnējās līnijas

Tāpēc
,
, no šejienes.

Apsveriet trīsdimensiju Eiklīda telpu ﻉ. Ļaujiet punktu
ﻉ un plakne ﻉ. Noskaidrosim attālumu no šī punkta
uz plakni , kas dota ar vienādojumu (V.9. att.).

Līdzīgi mums ir divdimensiju telpai
un vektors
, ak, no šejienes

.

(V.13)
Un
Mēs rakstām taisnes vienādojumu, kas satur perpendikulāru plaknei  kā taisnes vienādojumu, kas iet caur diviem punktiem

, guļ lidmašīnā:

.
(V.14)

Lai atrastu punkta koordinātas ,,jebkurām divām formulas (V.14) vienādībām pievienojam vienādojumu
Atrisinot trīs vienādojumu sistēmu (V.14), (V.15), mēs atrodam

.

– punktu koordinātas
. Tad perpendikula vienādojums tiks ierakstīts formā

Lai atrastu attālumu no punkta

uz plakni formulas (V.13) vietā izmantojam

Divu plakņu krustošanās taisni nosaka divi punkti, no kuriem katrs pieder abām plaknēm, vai viens punkts, kas pieder divām plaknēm, un zināmais taisnes virziens. Abos gadījumos uzdevums ir atrast punktu, kas kopīgs abām plaknēm. Vispārējā tehnika divu plakņu krustošanās līnijas izveidošanai ir šāda. Tiek ieviesta palīgplakne, tiek konstruētas palīgplaknes krustošanās līnijas ar divām dotajām, un konstruēto līniju krustpunktā tiek atrasts abu plakņu kopējais punkts. Lai atrastu otro kopīgo punktu, konstrukciju atkārto, izmantojot citu palīgplakni. 5. attēlā parādīts krustojuma līnijas vizuāls attēlojums K 1 K 2 Un J.

divas lidmašīnas

R K 1 K 2 Un J 5. attēls S Plakņu krustošanās līnijas pirmā kopīgā punkta konstrukcijas vizuālam attēlojumam K 1 K 2(6. attēls) ir ieviesta palīgplakne 1-2 . Ar lidmašīnu J tas krustojas pa līniju 3-4 , ar lidmašīnu 1-2 Un 3-4 – pa līniju . Līniju krustpunktā noteikts pirmais kopīgais punkts K 1 K 2 K 1 divas lidmašīnas Un

J

– to krustojuma līnijas pirmais punkts.

Līdzīgi tiek ieviesta jauna griešanas plakne un konstruēts krustojuma līnijas otrais punkts.

Piemēram, 7. attēlā parādīta izvirzījumu konstrukcija m"n", mn krustojuma līnijas MN frontālās projekcijas plakne K 1 K 2 ar trīsstūra plakni ABC.

7. attēls

Uz frontālās projekcijas projekciju krustpunktā a"b" Un a"c" ar pēdām P u atrast frontālās projekcijas m" Un n" divi kopīgi punkti dotajām plaknēm. Pamatojoties uz tiem, tika izveidotas horizontālās projekcijas m Un n uz horizontālām projekcijām ab K 1 ac trijstūra malas. Caur punktiem m Un n Mēs uzzīmējam plakņu krustošanās līnijas horizontālu projekciju. Skatoties gar bultiņu S no frontālās projekcijas redzams, ka daļa no trijstūra atrodas pa kreisi no krustojuma līnijas MN(m"n") atrodas virs plaknes K 1 K 2, t.i., redzams, pārējais atrodas zem lidmašīnas R, t.i., neredzams (sadaļa mbcn parādīts ar pārtrauktu līniju).

Vēl viens piemērs divu trīsstūrveida plākšņu krustošanās līnijas konstruēšanai ABC Un DEF, no kuriem viens ( DEF) ir norādīta kā horizontāli izvirzīta plakne, kas parādīta 8. attēlā.

8. attēls

Uz horizontālas projekcijas horizontālo projekciju krustpunktā ab Un bc ballītēm DABC ar projekciju dfe no otrā trīsstūra atrodam horizontālās projekcijas m Un n to krustošanās punkti. Saskaņā ar tiem uz sānu frontālajām projekcijām a"b" Un b"c" frontālo projekciju konstruēšana m" Un n" krustojuma punkti MN. Frontālajā projekcijā mēs atzīmējam trīsstūru daļu redzamību, vadoties pēc sekojošā: skatoties pa bultiņu S no horizontālās projekcijas ir acīmredzams, ka sānu AC atrodas trijstūra plaknes priekšā DEF.

Tāpēc sānu AC un tā ierobežotā trijstūra daļa ABC līdz krustojuma līnijai MN redzams (t.i., ir redzama četrstūra frontālā projekcija a"c"n"m"). Redzamā frontālās projekcijas daļa DDEFēnots zīmējumā.

Plakņu krustošanās līnijas uzbūve vispārējā stāvoklī. 9. attēlā parādīta izvirzījumu konstrukcija m"n", mn divu plakņu krustošanās līnijas, no kurām viena ir noteikta ar projekcijām a"b", b"c", ab, bc divas krustojošas līnijas, otra - projekcijas d"e", f"g", de, fg divas paralēlas līnijas.

Divas horizontālas plaknes, kas noteiktas ar pēdām, tiek ņemtas par palīgplaknēm R u Un T u .

Lidmašīna Ršķērso pirmo doto plakni taisnā līnijā 1-2 , otrais - taisnā līnijā 3-4 . Saskaņā ar frontālajām projekcijām 1", 2" Un 3", 4" mēs atrodam horizontālās projekcijas, izmantojot sakaru līnijas 1, 2 Un 3, 4 uz horizontālām projekcijām ab, bc, de, fg taisni Caur tiem mēs zīmējam līniju horizontālās projekcijas 1-2 Un 3-4 krustojuma līnijas. Atzīmējiet punktu m– kopīga punkta horizontālā projekcija M trīs plaknes - divas dotās un palīgierīces R. Izmantojot to, mēs nosakām frontālo projekciju m" uz frontālās trases R u palīgplakne.

9. attēls

Palīglidmašīnas T Un R paralēli. Arī to krustošanās līnijas ar dotajām plaknēm ir paralēlas. Tāpēc plaknes krustošanās līniju horizontālās projekcijas T ar dotajām plaknēm tiek novilktas caur projekciju b paralēli projekcijai 1-2 un caur projekciju 5 paralēli projekcijai 3-4 . Viņu krustojumā tika atrasta horizontāla projekcija n trīs plakņu otrais kopīgais punkts, t.i. divu doto plakņu krustošanās līnijas. Pa to pa frontālo taku T u frontālā projekcija ir konstruēta uz palīgplaknes n". Caur konstruētajām projekcijām m",n" Un m, n Mēs veicam vēlamās krustojuma līnijas frontālās un horizontālās projekcijas MN.

Divas plaknes krustojas viena ar otru taisnā līnijā. Lai to konstruētu, ir jānosaka divi punkti, kas vienlaikus pieder katrai no dotajām plaknēm. Apskatīsim, kā tas tiek darīts, izmantojot šādus piemērus.

Atradīsim vispārīgo plakņu α un β krustošanās līniju gadījumam, kad pl. α ir dota ar trijstūra ABC projekcijām, un pl. β – paralēlas taisnes d un e. Šīs problēmas risinājums tiek veikts, konstruējot punktus L 1 un L 2, kas pieder pie krustojuma līnijas.

Risinājums

1. Mēs ieviešam papildu horizontālo plakni γ 1. Tas krusto α un β pa taisnām līnijām. Šo līniju frontālās projekcijas 1""C"" un 2""3" sakrīt ar kvadrāta frontālo trasi. γ 1. Attēlā tas ir apzīmēts kā f 0 γ 1 un atrodas paralēli x asij.
2. Mēs nosakām horizontālās projekcijas 1"C" un 2"3" gar sakaru līnijām.
3. Atrodam L 1 horizontālo projekciju līniju 1 "C" un 2 "3" krustpunktā. Punkta L 1 frontālā projekcija atrodas uz plaknes γ frontālās trases.
4. Mēs ieviešam papildu horizontālo plakni γ 2. Izmantojot konstrukcijas, kas līdzīgas 1., 2., 3. punktā aprakstītajām, atrodam L 2. punkta projekcijas.
5. Caur L 1 un L 2 novelkam vajadzīgo taisni l.

Ir vērts atzīmēt, ka kā pl. γ ir ērti izmantot gan līmeņa plaknes, gan projekcijas plaknes.

Atradīsim plakņu α un β krustošanās līniju, ko nosaka pēdas. Šis uzdevums ir daudz vienkāršāks nekā iepriekšējais. Tam nav nepieciešama palīgplakņu ieviešana. To lomu spēlē projekcijas plaknes P 1 un P 2.

Konstrukcijas algoritms

1. Mēs atrodam punktu L" 1, kas atrodas horizontālo trašu h 0 α un h 0 β krustpunktā. Punkts L"" 1 atrodas uz x ass. Tā pozīciju nosaka, izmantojot savienojuma līniju, kas novilkta no L" 1 .
2. Atrodam punktu L"" 2 frontālo pēdu pl. krustojumā. α un β. Punkts L" 2 atrodas uz x ass. Tā atrašanās vieta tiek noteikta gar savienojuma līniju, kas novilkta no L"" 2.
3. Mēs velkam taisnas līnijas l" un l"" caur atbilstošajām punktu L 1 un L 2 projekcijām, kā parādīts attēlā.

Tādējādi taisne l, kas iet caur plakņu pēdu krustošanās punktiem, ir vēlamā.

Trijstūra plakņu krustpunkts

Apsvērsim ar trijstūriem ABC un DEF noteikto plakņu krustošanās līnijas konstruēšanu un to redzamības noteikšanu, izmantojot konkurējošo punktu metodi.

Konstrukcijas algoritms

1. Caur taisni DE novelkam frontāli izvirzīto plakni σ: tās trase f 0σ ir norādīta zīmējumā. Plakne σ šķērso trijstūri ABC pa taisni 35. Atzīmējot punktus 3""=A""B""∩f 0σ un 5""=A""С""∩f 0σ, nosaka pozīciju (∙). )3" un (∙) 5" pa sakaru līnijām pie ΔA"B"C.
2. Atrodam palīgplaknē σ esošās taisnes DE un 35 krustpunkta N horizontālo projekciju N"=D"E"∩3"5". Projekcija N"" atrodas uz frontālās trases. f 0σ tajā pašā savienojuma līnijā ar N".

Caur taisni BC novelkam frontāli izvirzīto plakni τ: tās trase f 0τ ir norādīta zīmējumā. Izmantojot konstrukcijas, kas līdzīgas algoritma 1. un 2. punktā aprakstītajām, atrodam punkta K projekcijas.

3. Caur N un K novelkam vajadzīgo taisni NK - ΔABC un ΔDEF krustošanās līniju.

Redzamības definīcija

Frontāli konkurējošie punkti 4 un 5, kas pieder attiecīgi ΔDEF un ΔABC, atrodas uz vienas frontāli izvirzītās taisnes, bet atrodas dažādos attālumos no projekcijas plaknes π 2 . Tā kā (∙)5" ir tuvāk novērotājam nekā (∙)4", nodalījums ΔABC ar tā (∙)5 ir redzams projekcijā uz kvadrātu. π 2. Līnijas N""K"" pretējā pusē mainās trīsstūru redzamība.

Horizontāli konkurējošie punkti 6 un 7, kas pieder attiecīgi ΔABC un ΔDEF, atrodas uz vienas horizontāli izvirzītas taisnes, bet atrodas dažādos attālumos no projekcijas plaknes π 1 . Tā kā (∙)6"" atrodas augstāk par (∙)7"", tad nodalījums ΔABC ar tā (∙)6 ir redzams projekcijā uz kvadrātu. π 1. Līnijas N"K" pretējā pusē mainās trīsstūru redzamība.