Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям. Так, прямая K 1 К 2 (рис. 163), по которой пересекаются между собой плоскость, заданная треугольником АВС, и пл. β, заданная прямыми DE и DF, проходит через точки K 1 и K 2 ; но в этих точках прямые АВ и АС первой плоскости пересекают пл. β т. е. точки К 1 и К 2 принадлежат обеим плоскостям.

Следовательно, в общем случае для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям; эти точки определяют линию пересечения плоскостей.

Для нахождения каждой из таких двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна к плоскости проекций, то построение проекций линии пересечения упрощается. Начнем с такого случая.

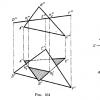
На рис. 164 показано пересечение двух плоскостей, из которых одна (заданная треугольником DEF) расположена перпендикулярно к пл. π 2 . Так как треугольник DEF проецируется на пл.π 2 в виде прямой линии (D"F"), то фронтальная проекция отрезка прямой, по которому пересекаются оба треугольника, представляет собой отрезок К" 1 К" 2 на проекции D"F". Дальнейшее построение ясно из чертежа.

Другой пример дан на рис. 165. Горизонтально-проецирующая плоскость α пересекает плоскость треугольника АВС. Горизонтальная проекция линии пересечения этих плоскостей - отрезок M"N" - определяется на следе α".

Теперь рассмотрим общий случай построения линии пересечения двух плоскостей . Пусть одна из плоскостей, β, задана двумя пересекающимися прямыми, а другая, γ,- двумя параллельными прямыми. Построение показано на рис. 166. В результате взаимного пересечения плоскостей β и γ получена прямая K 1 K 2 . Выразим это записью: β × γ = К 1 K 2 .

Для определения положения точек K 1 и К 2 возьмем две вспомогательные фронтально-проецирующие плоскости (α 1 , и α 2), пересекающие каждую из плоскостей β и γ. При пересечении плоскостей β и γ плоскостью α 1 . получаем прямые с проекциями 1"2", 1"2" и 3"4", 3"4". Эти прямые, расположенные в пл. α 1 , в своем пересечении определяют первую точку, К 1 , линии пересечения плоскостей β и γ.

Получив проекции К" 1 и К" 2 находим на следах и α" 1 и α" 2 проекции К" 1 и К" 2 . Этим определяются проекции К" 1 К" 2 и К" 1 К" 2 искомой прямой пересечения плоскостей β и γ(проекции проведены штрихпунктирной линией).

При построении можно иметь в виду следующее: так как вспомогательные секущие плоскости α 1 и α 2 взаимно параллельны, то, построив проекции 1"2" и 3"4" следует для проекций 5"6" и 7"8" взять по одной точке, хотя бы 5 и 8, так как 5"6"||1"2" и 7"8"||3"4".

В рассмотренном построении были взяты в качестве вспомогательных две фронгально- проецирующие плоскости. Конечно, можно было взять и иные плоскости, например две горизонтальные или одну горизонтальную, другую фронтальную и т. д. Сущность построений от этого не меняется. Однако может встретиться такой случай. Положим, что были взяты в качестве вспомогательных две горизонтальные плоскости и полученные при пересечении ими

плоскостей β и γ горизонтали оказались взаимно параллельными. Но рис. 167 показывает, что β и γ пересекаются между собой, хотя их горизонтали параллельны. Следовательно, получив взаимно параллельные горизонтальные проекции горизонталей АВ и CD и зная, что плоскости при этом не обязательно параллельны, а могут пересекаться (по общей для них горизонтали), надо испытать плоскости β и γ при помощи хотя бы, горизонгально-проецирующей плоскости (см. рис. 167); если прямые, по которым эта вспомогательная плоскость σ, пересечет β и γ, также оказались бы параллельны одна другой, то плоскости β и γ не пересекаются, а параллельны одна другой. На рис. 167 эти прямые пересекаются в точке К, через которую и проходит линия пересечения плоскостей β и γ параллельно прямым ВА и CD.

Если плоскости заданы их следами на плоскостях проекций, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей (рис. 168): прямая, проходящая через эти точки, является общей для обеих плоскостей, т. е. их линией пересечения.

Схему построения линии пересечения двух плоскостей (см. рис. 166) можно, конечно, распространить и на случай задания плоскостей их следами. Здесь роль вспомогательных секущих плоскостей исполняют сами плоскости проекций:

α × π 1 =h" 0α ; β× π 1 =h" 0β ; h" 0α × h" 0β =M;

α × π 2 =f" 0α ; β× π 2 =f" 0β ; f" 0α × f" 0β =N.

Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей. Поэтому для построения проекций линии пересечения плоскостей α и β (рис. 168) надо: 1) найти точку М" в пересечении следов h" 0α и h" 0β

и точку N" в пересечении f" 0α и f" 0β , а по ним - проекции М" и N"; 2) провести прямые линии M"N" и M"N",

На рис. 169-171 показаны случаи, когда известно направление линии пересечения. Поэтому достаточно иметь лйшь одну точку от пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов.

Вопросы к §§ 22-24

1. Какое взаимное положение могут занимать две плоскости?
2. Каков признак параллельности двух плоскостей?
3. Как взаимно располагаются фронтальные следы двух параллельных между собой фронтально-проецирующих плоскостей?
4. Как взаимно располагаются горизонтальные следы двух параллельных между собой горизонтально-проецирующих плоскостей?
5. Как взаимно располагаются одноименные следы двух параллельных между собой плоскостей?
6. Служит ли признаком взаимного пересечения двух плоскостей пересечение хотя бы одной пары их одноименных следов?
7. Как установить взаимное положение прямой и Плоскости?
8. Как строится точка пересечения прямой линии с плоскостью, перпендикулярной к одной или к двум плоскостям проекций?
9. Какая точка из числа расположенных на общем перпендикуляре к а) пл. π 1 б) пл. π 2 считается видимой соответственно на π 1 , на π 2 ?
10. Как строится линия пересечения двух плоскостей, из которых хотя бы одна перпендикулярна к пл. π 1 или к пл. π 2 ?
11. В чем заключается общий способ построения линии пересечения двух плоскостей?

Пример построения линии пересечения двух плоскостей способом секущих плоскостей посредников представлен на рисунке 1.3.25. Плоскость S определяется пересекающимися прямыми а и b , а плоскость Q – параллельными прямыми с и d .

Для нахождения линии l пересечения плоскостей S и Q проведём две фронтально проецирующие плоскости W (W 2 ) и W¢ (W¢ 2 ), являющиеся посредниками. Плоскость W пересекает данные плоскости S и Q по прямым линиям 1-2 (1 2 -2 2 , 1 1 -2 1 ) и 3-4 (3 2 -4 2 , 3 1 -4 1 ). Точку пересечения этих прямых обозначим через К (К 1 , К 2 ). Точка К принадлежит одновременно трём плоскостям S, Q, W. Следовательно, точка К S и Q. Плоскость W¢ пересекает плоскости S и Q по прямым линиям 5-6 (5 1 -6 1 , 5 2 -6 2 ) и 7-8 (7 1 -8 1 , 7 2 -8 2 ). Точкой пересечения этих линий является точка К¢ . Она, как и точка К принадлежит линии пересечения плоскостей S и Q . Следовательно, прямая l , проходящая через точки К и К¢ , есть искомая прямая пересечения данных плоскостей S и Q .

Рисунок 1.3.26 – Пересечение двух плоскостей общего положения

На рисунке 1.3.26 представлен пример построения линии пересечения двух плоскостей способом пересечения прямой линии с плоскостью. Плоскости заданы треугольниками АВС и EGF . Вспомогательные секущие плоскости S (S 2 ) и S¢ (S 2 ) проведены через стороны EG и ВС треугольников. Плоскость S (S 2 ) пересекает треугольник АВС по прямой 1-2 . Точка К EG и 1-2 . Плоскость S¢ (S¢ 2 ) пересекает треугольник EGF по прямой 3-4 . Точка К¢ является результатом пересечения прямых ВС и 3-4 . Точки К и К¢ ограничивают отрезок искомой линии пересечения, находящийся в пределах обоих треугольников.

Относительная видимость треугольников определена на фронтальной проекции с помощью конкурирующих точек 2 и 4 , из которых точка 4 стороны EG закрывает собой точку 2 стороны ВС . Видимость на горизонтальной плоскости проекций определена с помощью конкурирующих точек 5 и 6 , из которых точка 6 стороны EG закрывает собой точку 5 стороны АС .

Кривые линии

Кривую линию можно рассматривать как след движущейся точки. Эта точка может быть отдельной точкой или точкой, принадлежащей движущейся в пространстве линии или поверхности.

Кривые линии могут быть образованы пересечением кривой поверхности плоскостью (в общем случае), взаимным пересечением двух поверхностей, из которых хотя бы одна является кривой.

Законом образования кривой линии называется совокупность условий, определяющих эту линию. Точка, линия, поверхность перемещаются в пространстве, подчиняясь разным условиям. Плоскость может пересекать разнообразные кривые поверхности по самым различным направлениям. Взаимно пересекаться могут самые разнообразные поверхности при различном положении их относительно друг друга. Отсюда следует, что образование кривой линии может подчиняться бесчисленному множеству условий и может быть образовано бесчисленное множество кривых линий. Кроме того, одна и та же кривая линия может быть образована различными способами.

Например, эллипс может быть образован движением точки в плоскости, при котором в каждый данный момент сумма расстояний от этой точки до двух других неподвижных точек – фокусов эллипса – постоянна и равна большой оси эллипса. Но эллипс может быть образован и пересечением кругового цилиндра с плоскостью, расположенной произвольно по отношению к его оси или полным пересечением поверхностей двух круговых цилиндров одинакового диаметра.

Все кривые линии по положению их точек в пространстве делятся на два вида: плоские кривые – кривые, все точки которых лежат в одной плоскости (например, окружность, эллипс, парабола и т.д.) и пространственные кривые – кривые, точки которых не лежат в одной плоскости, например, винтовая линия

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и, то есть как множество точек, удовлетворяющих системе двух линейных уравнений

(V.5)

Справедливо и обратное утверждение: система двух независимых линейных уравнений вида (V.5) определяет прямую как линию пересечения плоскостей (если они не параллельны). Уравнения системы (V.5) называются общим уравнением прямой в пространстве
.

Пример V .12 . Составить каноническое уравнение прямой, заданной общими уравнениями плоскостей

Решение . Чтобы написать каноническое уравнение прямой или, что тоже самое, уравнение прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например Oyz и Oxz .

Точка пересечения прямой с плоскостью Oyz имеет абсциссу
. Поэтому, полагая в данной системе уравнений
, получим систему с двумя переменными:

Ее решение
,
вместе с
определяет точку
искомой прямой. Полагая в данной системе уравнений
, получим систему

решение которой
,
вместе с
определяет точку
пересечения прямой с плоскостьюOxz .

Теперь запишем уравнения прямой, проходящей через точки
и
:
или
, где
будет направляющим векто-ром этой прямой.

Пример V .13. Прямая задана каноническим уравнением
. Составить общее уравнение этой прямой.

Решение. Каноническое уравнение прямой можно записать в виде системы двух независимых уравнений:



Получили общее уравнение прямой, которая теперь задана пересечением двух плоскостей, одна из которых
параллельна осиOz (
), а другая
– осиОу (
).

Данную прямую можно представить в виде линии пересечения двух других плоскостей, записав ее каноническое уравнение в виде другой пары независимых уравнений:



Замечание . Одна и та же прямая может быть задана различными системами двух линейных уравнений (то есть пересечением различных плоскостей, так как через одну прямую можно провести бесчисленное множество плоскостей), а также различными каноническими уравнениями (в зависимости от выбора точки на прямой и ее направляющего вектора).

Ненулевой вектор, параллельный прямой линии, будем называть ее направляющим вектором .

Пусть в трехмерном пространстве задана прямая l , проходящая через точку
, и ее направляющий вектор
.

Любой вектор
, где
, лежащий на прямой, коллинеарен с вектором, поэтому их координаты пропорциональны, то есть

. (V.6)

Это уравнение называется каноническим уравнением прямой. В частном случае, когда ﻉ есть плоскость, получаем уравнение прямой на плоскости

. (V.7)

Пример V .14. Найти уравнение прямой, проходящей через две точки
,
.

,

где
,
,
.

Удобно уравнение (V.6) записать в параметрической форме. Так как координаты направляющих векторов параллельных прямых пропорциональны, то, полагая

,

где t – параметр,
.

Расстояние от точки до прямой

Рассмотри двухмерное евклидовое пространство ﻉ с декартовой системой координат. Пусть точка
ﻉ и l ﻉ. Найдем расстояние от этой точки до прямой. Положим
, и прямая l задается уравнением
(рис.V.8).

Расстояние
, вектор
, где
– нормальный вектор прямой l ,
и – коллинеарны, поэтому их координаты пропорциональны, то есть
, следовательно,
,
.

Отсюда
или умножая эти уравнения наA и B соответственно и складывая их, находим
, отсюда

.

(V.8)

определяет расстояние от точки
до прямой
.

Пример V .15. Найти уравнение прямой, проходящей через точку
перпендикулярно прямойl :
и найти расстояние от
до прямойl .

Из рис. V.8 имеем
, а нормальный вектор прямойl
. Из условия перпендикулярности имеем

Так как
, то

. (V.9)

Это и есть уравнение прямой, проходящей через точку
,перпендикулярно прямой
.

Пусть имеем уравнение прямой (V.9), проходящей через точку
, перпендикулярна прямойl :
. Найдем расстояние от точки
до прямойl , используя формулу (V.8).

Для нахождения искомого расстояния достаточно найти уравнение прямой, проходящей через две точки
и точку
, лежащую на прямой в основании перпендикуляра. Пусть
, тогда

Так как
, а вектор
, то

. (V.11)

Поскольку точка
лежит на прямойl , то имеем еще одно равенство
или

Приведем систему к виду, удобному для применения метода Крамера

Ее решение имеет вид

,

. (V.12)

Подставляя (V.12) в (V.10), получаем исходное расстояние.

Пример V .16. В двухмерном пространстве задана точка
и прямая
. Найти расстояние от точки
до прямой; записать уравнение прямой, проходящей через точку
перпендикулярно заданной прямой и найти расстояние от точки
до основания перпендикуляра к исходной прямой.

По формуле (V.8) имеем

Уравнение прямой, содержащей перпендикуляр, найдем как прямую, проходящую через две точки
и
, воспользовавшись формулой (V.11). Так как
, то, с учетом того, что
, а
, имеем

.

Для нахождения координат
имеем систему с учетом того, что точка
лежит на исходной прямой

Следовательно,
,
, отсюда.

Рассмотрим трехмерное евклидовое пространство ﻉ. Пусть точка
ﻉ и плоскость ﻉ. Найдем расстояние от этой точки
до плоскости, заданной уравнением (рис.V.9).

Аналогично двухмерному пространству имеем
и вектор
, а, отсюда

. (V.13)

Уравнение прямой, содержащей перпендикуляр к плоскости , запишем как уравнение прямой, проходящей через две точки
и
, лежащую в плоскости:

. (V.14)

Для нахождения координат точки
к двум любым равенствам формулы (V.14) добавим уравнение

Решая систему трех уравнений (V.14), (V.15), найдем ,,– координаты точки
. Тогда уравнение перпендикуляра запишется в виде

.

Для нахождения расстояния от точки
до плоскости вместо формулой (V.13) воспользуемся

Прямая линия пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям, или одной точкой, принадлежащей двум плоскостям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух плоскостей.

Общий прием построения линии пересечения двух плоскостей заключается в следующем. Вводят вспомогательную плоскость, строят линии пересечения вспомогательной плоскости с двумя заданными и в пересечении построенных линий находят общую точку двух плоскостей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной плоскости.

На рисунке 5 показано наглядное изображение линии пересечения K 1 K 2 двух плоскостей Р и Q .

Рисунок 5

Для наглядного изображения построения первой общей точки линии пересечения плоскостей Р и Q (рисунок 6) введена вспомогательная плоскость S . С плоскостью Р она пересекается по линии 1-2 , с плоскостью Q – по линии 3-4 . В пересечении линий 1-2 и 3-4 определена первая общая точка K 1 двух плоскостей Р и Q – первая точка линии их пересечения.

Аналогично вводят новую секущую плоскость и строят вторую точку линии пересечения.

Рисунок 6

Частный случай построения линии пересечения двух плоскостей, когда одна из них проецирующая. В этом случае построение линии пересечения упрощается тем, что одна ее проекция совпадает с проекцией проецирующей плоскости на ту плоскость проекций, к которой она перпендикулярна.

В качестве примера на рисунке 7 показано построение проекций m"n", mn линии пересечения MN фронтально-проецирующей плоскости Р с плоскостью треугольника АВС .

Рисунок 7

На фронтальной проекции в пересечении проекций a"b" и а"с" со следом Р u находим фронтальные проекции m" и n" двух общих точек заданных плоскостей. По ним построены горизонтальные проекции m и n на горизонтальных проекциях аb и ас сторон треугольника. Через точки m и n проводим горизонтальную проекцию линии пересечения плоскостей. При взгляде по стрелке S по фронтальной проекции очевидно, что часть треугольника левее линии пересечения MN (m"n" ) находится над плоскостью Р , т. е. видима, остальная часть - под плоскостью Р , т. е. невидима (участок mbcn показан штриховой линией).

Другой пример построения линии пересечения двух треугольных пластин АВС и DEF , одна из которых (DEF ) задана как горизонтально-проецирующая плоскость, приведен на рисунке 8.

Рисунок 8

На горизонтальной проекции в пересечении горизонтальных проекций ab и bc сторон DАВС с проекцией dfe второго треугольника находим горизонтальные проекции m и n точек их пересечения. По ним на фронтальных проекциях сторон а"b" и b"c" строим фронтальные проекции m" и n" точек линии пересечения MN . На фронтальной проекции отмечаем видимость частей треугольников, руководствуясь следующим: при взгляде по стрелке S по горизонтальной проекции очевидно, что сторона АС находится перед плоскостью треугольника DEF .

Следовательно, сторона АС и ограничиваемая ею часть треугольника АВС до линии пересечения MN видимы (т. е. видима фронтальная проекция четырехугольника a"c"n"m" ). Видимая часть фронтальной проекции DDEF на чертеже оттенена.

Построение линии пересечения плоскостей общего положения. На рисунке 9 приведено построение проекций m"n", mn линии пересечения двух плоскостей, одна из которых задана проекци­ями а"b", b"c", ab, bc двух пересекающихся прямых, другая - проекциями d"e", f"g", de, fg двух параллельных прямых.

В качестве вспомогательных плоскостей взяты две горизонтальные плоскости, заданные следами R u и Т u .

Плоскость R пересекает первую заданную плоскость по прямой 1-2 , вторую – по прямой 3-4 . По фронтальным проекциям 1", 2" и 3", 4" находим с помощью линий связи горизонтальные проекции 1, 2 и 3, 4 на горизонтальных проекциях ab, bc, de, fg прямых. Через них проводим горизонтальные проекции линий 1-2 и 3-4 линий пересечения. Отмечаем точку m – горизонтальную проекцию общей точки M трех плоскостей – двух заданных и вспомогательной R . По ней определяем фронтальную проекцию m" на фронтальном следе R u вспомогательной плоскости.

Рисунок 9

Вспомогательные плоскости Т и R параллельны. Линии их пересечения с заданными плоскостями также параллельны. Поэтому горизонтальные проекции линий пересечения плоскости Т c заданными плоскостями проведены через проекцию b параллельно проекции 1-2 и через проекцию 5 параллельно проекции 3-4 . В их пересечении найдена горизонтальная проекция n второй общей точки трех плоскостей, т.е. линии пересечения двух заданных плоскостей. По ней на фронтальном следе T u вспомогательной плоскости построена фронтальная проекция n" . Через построенные проекции m", n" и m, n проводим фронтальную и горизонтальную проекции искомой линии пересечения MN .

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L 1 и L 2 , принадлежащих линии пересечения.

Решение

1. Вводим вспомогательную горизонтальную плоскость γ 1 . Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1""C"" и 2""3"", совпадают с фронтальным следом пл. γ 1 . Он обозначен на рисунке как f 0 γ 1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1"C" и 2"3" по линиям связи.
3. Находим горизонтальную проекцию точки L 1 на пересечении прямых 1"C" и 2"3". Фронтальная проекция точки L 1 лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ 2 . С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L 2 .
5. Через L 1 и L 2 проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П 1 и П 2 .

Алгоритм построения

1. Находим точку L" 1 , расположенную на пересечении горизонтальных следов h 0 α и h 0 β . Точка L"" 1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L" 1 .
2. Находим точку L"" 2 на пересечении фронтальных следов пл. α и β. Точка L" 2 лежит на оси x. Её положение определяется по линии связи, проведенной из L"" 2 .
3. Проводим прямые l" и l"" через соответствующие проекции точек L 1 и L 2 , как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

Алгоритм построения

1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f 0σ . Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3""=A""B""∩f 0σ и 5""=A""С""∩f 0σ , определяем положение (∙)3" и (∙)5" по линиям связи на ΔA"B"C".
2. Находим горизонтальную проекцию N"=D"E"∩3"5" точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N"" расположена на фронтальном следе f 0σ на одной линии связи с N".

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f 0τ . С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

3. Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.

Определение видимости

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π 2 . Так как (∙)5" находится ближе к наблюдателю, чем (∙)4", то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π 2 . С противоположной стороны от линии N""K"" видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π 1 . Так как (∙)6"" находится выше, чем (∙)7"", то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π 1 . С противоположной стороны от линии N"K" видимость треугольников меняется.