วิธีขยายฐานของลอการิทึม ลอการิทึม - คุณสมบัติ สูตร กราฟ ตัวอย่างง่ายๆ พร้อมลอการิทึม
เมื่อสังคมพัฒนาและการผลิตมีความซับซ้อนมากขึ้น คณิตศาสตร์ก็พัฒนาขึ้นด้วย การเคลื่อนไหวจากง่ายไปสู่ซับซ้อน จากการบัญชีทั่วไปโดยใช้วิธีการบวกและการลบด้วยการทำซ้ำซ้ำ ๆ เรามาถึงแนวคิดของการคูณและการหาร การลดการดำเนินการคูณซ้ำๆ กลายเป็นแนวคิดเรื่องการยกกำลัง ตารางแรกของการพึ่งพาตัวเลขบนฐานและจำนวนการยกกำลังถูกรวบรวมในศตวรรษที่ 8 โดย Varasena นักคณิตศาสตร์ชาวอินเดีย จากนั้นคุณสามารถนับเวลาที่เกิดลอการิทึมได้
ภาพสเก็ตช์ประวัติศาสตร์
การฟื้นตัวของยุโรปในศตวรรษที่ 16 ยังช่วยกระตุ้นการพัฒนากลศาสตร์อีกด้วย ต ต้องใช้การคำนวณจำนวนมากเกี่ยวข้องกับการคูณและการหารตัวเลขหลายหลัก โต๊ะโบราณก็บริการดีมาก พวกเขาทำให้สามารถแทนที่การดำเนินการที่ซับซ้อนด้วยการดำเนินการที่ง่ายกว่า - การบวกและการลบ ก้าวสำคัญไปข้างหน้าคือผลงานของนักคณิตศาสตร์ Michael Stiefel ซึ่งตีพิมพ์ในปี 1544 ซึ่งเขาตระหนักถึงความคิดของนักคณิตศาสตร์หลายคน สิ่งนี้ทำให้สามารถใช้ตารางได้ไม่เพียง แต่สำหรับกำลังในรูปแบบของจำนวนเฉพาะเท่านั้น แต่ยังรวมถึงค่าตรรกยะตามอำเภอใจด้วย
ในปี 1614 ชาวสก็อตแลนด์ จอห์น เนเปียร์ ซึ่งพัฒนาแนวคิดเหล่านี้ ได้แนะนำคำศัพท์ใหม่ว่า "ลอการิทึมของตัวเลข" เป็นครั้งแรก มีการรวบรวมตารางที่ซับซ้อนใหม่เพื่อคำนวณลอการิทึมของไซน์และโคไซน์ รวมถึงแทนเจนต์ สิ่งนี้ทำให้การทำงานของนักดาราศาสตร์ลดลงอย่างมาก
ตารางใหม่เริ่มปรากฏขึ้นซึ่งนักวิทยาศาสตร์ใช้สำเร็จมาเป็นเวลาสามศตวรรษ เวลาผ่านไปนานมากก่อนที่การดำเนินการใหม่ในพีชคณิตจะได้รูปแบบที่เสร็จสมบูรณ์ ให้คำจำกัดความของลอการิทึมและศึกษาคุณสมบัติของลอการิทึม
เฉพาะในศตวรรษที่ 20 เท่านั้นที่มีการถือกำเนิดขึ้นของเครื่องคิดเลขและคอมพิวเตอร์ มนุษยชาติจึงละทิ้งโต๊ะโบราณที่ทำงานอย่างประสบความสำเร็จตลอดศตวรรษที่ 13
 วันนี้เราเรียกลอการิทึมของ b ว่าเป็นฐานของ x ซึ่งเป็นกำลังของ a ที่ทำให้ b เขียนเป็นสูตร: x = log a(b)
วันนี้เราเรียกลอการิทึมของ b ว่าเป็นฐานของ x ซึ่งเป็นกำลังของ a ที่ทำให้ b เขียนเป็นสูตร: x = log a(b)
ตัวอย่างเช่น บันทึก 3(9) จะเท่ากับ 2 ซึ่งจะชัดเจนหากคุณปฏิบัติตามคำจำกัดความ ถ้าเรายก 3 ยกกำลัง 2 เราจะได้ 9
ดังนั้น คำจำกัดความที่จัดทำขึ้นจึงกำหนดข้อจำกัดเพียงข้อเดียว คือ ตัวเลข a และ b ต้องเป็นจำนวนจริง
ประเภทของลอการิทึม
คำจำกัดความแบบคลาสสิกเรียกว่าลอการิทึมจริง และจริงๆ แล้วคือคำตอบของสมการ a x = b ตัวเลือก a = 1 ถือเป็นเส้นเขตแดนและไม่เป็นที่สนใจ ข้อควรสนใจ: 1 กำลังใดๆ มีค่าเท่ากับ 1
มูลค่าที่แท้จริงของลอการิทึมกำหนดเฉพาะเมื่อฐานและอาร์กิวเมนต์มากกว่า 0 และฐานต้องไม่เท่ากับ 1
สถานที่พิเศษในสาขาคณิตศาสตร์เล่นลอการิทึม ซึ่งจะตั้งชื่อตามขนาดของฐาน:

กฎและข้อจำกัด
คุณสมบัติพื้นฐานของลอการิทึมคือกฎ: ลอการิทึมของผลิตภัณฑ์เท่ากับผลรวมลอการิทึม บันทึก abp = บันทึก ก(b) + บันทึก ก(p)
รูปแบบหนึ่งของคำสั่งนี้จะมี: log c(b/p) = log c(b) - log c(p) ฟังก์ชันผลหารจะเท่ากับผลต่างของฟังก์ชัน
จากกฎสองข้อก่อนหน้านี้ จะสังเกตได้ง่ายว่า: log a(b p) = p * log a(b)
คุณสมบัติอื่น ๆ ได้แก่ :

ความคิดเห็น ไม่จำเป็นต้องทำผิดพลาดทั่วไป - ลอการิทึมของผลรวมไม่เท่ากับผลรวมของลอการิทึม
 เป็นเวลาหลายศตวรรษแล้วที่การค้นหาลอการิทึมเป็นงานที่ค่อนข้างใช้เวลานาน นักคณิตศาสตร์ใช้สูตรที่รู้จักกันดีของทฤษฎีลอการิทึมของการขยายตัวพหุนาม:
เป็นเวลาหลายศตวรรษแล้วที่การค้นหาลอการิทึมเป็นงานที่ค่อนข้างใช้เวลานาน นักคณิตศาสตร์ใช้สูตรที่รู้จักกันดีของทฤษฎีลอการิทึมของการขยายตัวพหุนาม:
ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n) โดยที่ n คือจำนวนธรรมชาติที่มากกว่า 1 ซึ่งกำหนดความแม่นยำของการคำนวณ
ลอการิทึมที่มีฐานอื่นคำนวณโดยใช้ทฤษฎีบทเรื่องการเปลี่ยนจากฐานหนึ่งไปอีกฐานหนึ่งและคุณสมบัติของลอการิทึมของผลิตภัณฑ์
เนื่องจากวิธีนี้ใช้แรงงานเข้มข้นมากและ เมื่อแก้ไขปัญหาเชิงปฏิบัติยากต่อการนำไปใช้ เราใช้ตารางลอการิทึมที่คอมไพล์ไว้ล่วงหน้า ซึ่งทำให้งานทั้งหมดเร็วขึ้นอย่างเห็นได้ชัด
ในบางกรณีมีการใช้กราฟลอการิทึมที่ออกแบบมาเป็นพิเศษซึ่งให้ความแม่นยำน้อยกว่า แต่ช่วยเร่งการค้นหาได้อย่างมาก ค่าที่ต้องการ- เส้นโค้งของฟังก์ชัน y = log a(x) ซึ่งสร้างขึ้นบนหลายจุด ทำให้คุณสามารถใช้ไม้บรรทัดธรรมดาเพื่อค้นหาค่าของฟังก์ชันที่จุดอื่นได้ วิศวกรใช้สิ่งที่เรียกว่ากระดาษกราฟเพื่อจุดประสงค์เหล่านี้มาเป็นเวลานาน
ในศตวรรษที่ 17 เงื่อนไขการคำนวณแอนะล็อกเสริมครั้งแรกปรากฏขึ้นซึ่ง ศตวรรษที่ 19ได้รับการดูเสร็จแล้ว อุปกรณ์ที่ประสบความสำเร็จสูงสุดเรียกว่ากฎสไลด์ แม้จะมีความเรียบง่ายของอุปกรณ์ แต่รูปลักษณ์ภายนอกของมันช่วยเร่งกระบวนการคำนวณทางวิศวกรรมทั้งหมดได้อย่างมาก และนี่เป็นเรื่องยากที่จะประเมินค่าสูงไป ปัจจุบันมีเพียงไม่กี่คนที่คุ้นเคยกับอุปกรณ์นี้
การถือกำเนิดขึ้นของเครื่องคิดเลขและคอมพิวเตอร์ทำให้การใช้อุปกรณ์อื่นๆ ไร้จุดหมาย
สมการและอสมการ
ในการแก้สมการและอสมการต่างๆ โดยใช้ลอการิทึม จะใช้สูตรต่อไปนี้:
- การย้ายจากฐานหนึ่งไปอีกฐานหนึ่ง: log a(b) = log c(b) / log c(a);
- อันเป็นผลมาจากตัวเลือกก่อนหน้า: log a(b) = 1 / log b(a)
เพื่อแก้ความไม่เท่าเทียมกัน จะมีประโยชน์ที่จะรู้:
- ค่าลอการิทึมจะเป็นค่าบวกก็ต่อเมื่อฐานและอาร์กิวเมนต์มีค่ามากกว่าหรือน้อยกว่าหนึ่งเท่านั้น หากมีการละเมิดเงื่อนไขอย่างน้อยหนึ่งข้อ ค่าลอการิทึมจะเป็นลบ
- หากใช้ฟังก์ชันลอการิทึมกับด้านขวาและด้านซ้ายของอสมการ และฐานของลอการิทึมมากกว่า 1 แสดงว่าสัญญาณของอสมการยังคงอยู่ ไม่อย่างนั้นมันจะเปลี่ยนไป
ปัญหาตัวอย่าง
พิจารณาหลายตัวเลือกสำหรับการใช้ลอการิทึมและคุณสมบัติต่างๆ ตัวอย่างที่มีการแก้สมการ:

พิจารณาตัวเลือกในการวางลอการิทึมลงในกำลัง:
- ปัญหาที่ 3 คำนวณ 25^log 5(3) วิธีแก้ไข: ในเงื่อนไขของปัญหา รายการจะคล้ายกับรายการต่อไปนี้ (5^2)^log5(3) หรือ 5^(2 * log 5(3)) ลองเขียนให้แตกต่างออกไป: 5^log 5(3*2) หรือกำลังสองของตัวเลขเป็นอาร์กิวเมนต์ของฟังก์ชันสามารถเขียนเป็นกำลังสองของฟังก์ชันได้ (5^log 5(3))^2 การใช้คุณสมบัติของลอการิทึม นิพจน์นี้จะเท่ากับ 3^2 คำตอบ: จากการคำนวณเราได้ 9
การประยุกต์ใช้ในทางปฏิบัติ
เนื่องจากเป็นเครื่องมือทางคณิตศาสตร์ล้วนๆ จึงดูเหมือนห่างไกลจากความเป็นจริง ชีวิตจริงที่ลอการิทึมได้มาอย่างกะทันหัน คุ้มค่ามากเพื่ออธิบายวัตถุในโลกแห่งความเป็นจริง เป็นการยากที่จะหาวิทยาศาสตร์ที่ไม่ได้ใช้ สิ่งนี้ไม่เพียงนำไปใช้กับความรู้ทางธรรมชาติเท่านั้น แต่ยังรวมถึงสาขาความรู้ด้านมนุษยธรรมด้วย
การพึ่งพาลอการิทึม
นี่คือตัวอย่างบางส่วนของการขึ้นต่อกันของตัวเลข:

กลศาสตร์และฟิสิกส์
ในอดีต กลศาสตร์และฟิสิกส์ได้รับการพัฒนาโดยใช้วิธีการวิจัยทางคณิตศาสตร์มาโดยตลอด และในขณะเดียวกันก็ทำหน้าที่เป็นแรงจูงใจในการพัฒนาคณิตศาสตร์ รวมถึงลอการิทึมด้วย ทฤษฎีกฎฟิสิกส์ส่วนใหญ่เขียนด้วยภาษาคณิตศาสตร์ ขอให้เรายกตัวอย่างเพียงสองตัวอย่างในการอธิบายกฎฟิสิกส์โดยใช้ลอการิทึม
ปัญหาในการคำนวณปริมาณที่ซับซ้อนเช่นความเร็วของจรวดสามารถแก้ไขได้โดยใช้สูตร Tsiolkovsky ซึ่งวางรากฐานสำหรับทฤษฎีการสำรวจอวกาศ:
V = I * ln (M1/M2) โดยที่
- V คือความเร็วสุดท้ายของเครื่องบิน
- ฉัน – แรงกระตุ้นเฉพาะของเครื่องยนต์
- M 1 – มวลเริ่มต้นของจรวด
- M 2 – มวลสุดท้าย
อีกตัวอย่างที่สำคัญ- ใช้ในสูตรของนักวิทยาศาสตร์ผู้ยิ่งใหญ่อีกคนอย่าง Max Planck ซึ่งทำหน้าที่ประเมินสถานะสมดุลในอุณหพลศาสตร์
S = k * ln (Ω) โดยที่
- S – คุณสมบัติทางอุณหพลศาสตร์
- k – ค่าคงที่ของ Boltzmann
- Ω คือน้ำหนักทางสถิติของสถานะต่างๆ
เคมี
ไม่ชัดเจนคือการใช้สูตรในวิชาเคมีที่มีอัตราส่วนของลอการิทึม ขอยกตัวอย่างเพียงสองตัวอย่าง:
- สมการเนิร์นสต์ คือสภาวะของศักย์รีดอกซ์ของตัวกลางที่สัมพันธ์กับแอคติวิตีของสารและค่าคงที่สมดุล
- การคำนวณค่าคงที่เช่นดัชนีการสลายอัตโนมัติและความเป็นกรดของสารละลายก็ไม่สามารถทำได้หากไม่มีฟังก์ชันของเรา
จิตวิทยาและชีววิทยา
 และยังไม่ชัดเจนว่าจิตวิทยาเกี่ยวข้องกับเรื่องนี้อย่างไร ปรากฎว่าฟังก์ชั่นนี้อธิบายความแข็งแกร่งของความรู้สึกได้เป็นอย่างดี ความสัมพันธ์ผกผันค่าความเข้มของการกระตุ้นให้เป็นค่าความเข้มที่ต่ำกว่า
และยังไม่ชัดเจนว่าจิตวิทยาเกี่ยวข้องกับเรื่องนี้อย่างไร ปรากฎว่าฟังก์ชั่นนี้อธิบายความแข็งแกร่งของความรู้สึกได้เป็นอย่างดี ความสัมพันธ์ผกผันค่าความเข้มของการกระตุ้นให้เป็นค่าความเข้มที่ต่ำกว่า
หลังจากตัวอย่างข้างต้น จึงไม่น่าแปลกใจอีกต่อไปที่หัวข้อลอการิทึมมีการใช้กันอย่างแพร่หลายในวิชาชีววิทยา ปริมาตรทั้งหมดสามารถเขียนเกี่ยวกับรูปแบบทางชีววิทยาที่สอดคล้องกับเกลียวลอการิทึม
พื้นที่อื่นๆ
ดูเหมือนว่าการดำรงอยู่ของโลกจะเป็นไปไม่ได้หากปราศจากความเกี่ยวข้องกับหน้าที่นี้ และมันจะควบคุมกฎทั้งหมด โดยเฉพาะอย่างยิ่งเมื่อกฎแห่งธรรมชาติเกี่ยวข้องกับความก้าวหน้าทางเรขาคณิต คุ้มค่าที่จะหันมาใช้เว็บไซต์ MatProfi และมีตัวอย่างมากมายในกิจกรรมต่อไปนี้:

รายการสามารถไม่มีที่สิ้นสุด เมื่อเชี่ยวชาญหลักการพื้นฐานของฟังก์ชันนี้แล้ว คุณสามารถดำดิ่งสู่โลกแห่งปัญญาอันไม่มีที่สิ้นสุด
จุดเน้นของบทความนี้คือ ลอการิทึม- ที่นี่เราจะให้คำจำกัดความของลอการิทึม แสดงสัญกรณ์ที่ยอมรับ ยกตัวอย่างลอการิทึม และพูดคุยเกี่ยวกับลอการิทึมธรรมชาติและทศนิยม หลังจากนี้ เราจะพิจารณาเอกลักษณ์ลอการิทึมพื้นฐาน
การนำทางหน้า
ความหมายของลอการิทึม
แนวคิดของลอการิทึมเกิดขึ้นเมื่อแก้ปัญหาในแง่ผกผัน เมื่อคุณต้องการค้นหาเลขชี้กำลังจากค่าเลขชี้กำลังที่ทราบและฐานที่ทราบ
แต่พอคำนำก็ถึงเวลาตอบคำถาม “ลอการิทึม” คืออะไร? ให้เราให้คำจำกัดความที่เกี่ยวข้อง
คำนิยาม.
ลอการิทึมของ b ถึงฐาน aโดยที่ a>0, a≠1 และ b>0 เป็นเลขชี้กำลังที่คุณต้องเพิ่มจำนวน a เพื่อให้ได้ผลลัพธ์เป็น b
ในขั้นตอนนี้ เราสังเกตว่าคำว่า "ลอการิทึม" ในภาษาพูดควรทำให้เกิดคำถามตามมาสองข้อทันที: "จำนวนเท่าใด" และ "บนพื้นฐานใด" กล่าวอีกนัยหนึ่ง ไม่มีลอการิทึม มีแต่ลอการิทึมของตัวเลขจนถึงฐานบางฐานเท่านั้น
เข้าไปได้เลยทันที สัญกรณ์ลอการิทึม: ลอการิทึมของตัวเลข b ถึงฐาน a มักจะแสดงเป็น log a b ลอการิทึมของตัวเลข b ถึงฐาน e และลอการิทึมของฐาน 10 มีการกำหนดพิเศษของตัวเอง lnb และ logb ตามลำดับ นั่นคือ พวกมันเขียนไม่ใช่ log e b แต่เป็น lnb และไม่ใช่ log 10 b แต่เป็น lgb
ตอนนี้เราสามารถให้: .
และบันทึกต่างๆ  ไม่สมเหตุสมผลเลย เนื่องจากตัวแรกมีจำนวนลบอยู่ใต้เครื่องหมายลอการิทึม ตัวแรกมีจำนวนลบอยู่ในฐาน และตัวที่สามมีจำนวนลบอยู่ใต้เครื่องหมายลอการิทึมและมีหน่วยใน ฐาน
ไม่สมเหตุสมผลเลย เนื่องจากตัวแรกมีจำนวนลบอยู่ใต้เครื่องหมายลอการิทึม ตัวแรกมีจำนวนลบอยู่ในฐาน และตัวที่สามมีจำนวนลบอยู่ใต้เครื่องหมายลอการิทึมและมีหน่วยใน ฐาน
ตอนนี้เรามาพูดถึง กฎสำหรับการอ่านลอการิทึม- บันทึกสัญลักษณ์ a b อ่านว่า "ลอการิทึมของ b ถึงฐาน a" ตัวอย่างเช่น บันทึก 2 3 คือลอการิทึมของ 3 กำลังยกฐาน 2 และเป็นลอการิทึมของ 2 จุดสองในสามของรากที่สองฐานของ 5 ลอการิทึมฐาน e เรียกว่า ลอการิทึมธรรมชาติและสัญกรณ์ lnb อ่านว่า "ลอการิทึมธรรมชาติของ b" ตัวอย่างเช่น ln7 คือลอการิทึมธรรมชาติของ 7 และเราจะอ่านมันเป็นลอการิทึมธรรมชาติของ pi ลอการิทึมฐาน 10 มีชื่อพิเศษเช่นกัน - ลอการิทึมทศนิยมและ lgb อ่านว่า "ลอการิทึมฐานสิบของ b" ตัวอย่างเช่น lg1 คือลอการิทึมฐานสิบของหนึ่ง และ lg2.75 คือลอการิทึมฐานสิบของสองจุดเจ็ดห้าในร้อย
ควรพิจารณาแยกกันตามเงื่อนไข a>0, a≠1 และ b>0 ซึ่งให้คำจำกัดความของลอการิทึมไว้ ให้เราอธิบายว่าข้อจำกัดเหล่านี้มาจากไหน ความเท่าเทียมกันของรูปแบบที่เรียกว่า ซึ่งตามมาจากคำจำกัดความของลอการิทึมที่ระบุข้างต้นโดยตรง จะช่วยเราทำสิ่งนี้ได้
เริ่มจาก a≠1 กันก่อน เนื่องจากหนึ่งยกกำลังใด ๆ เท่ากับหนึ่ง ความเท่าเทียมกันจึงเป็นจริงได้เมื่อ b=1 เท่านั้น แต่บันทึก 1 1 อาจเป็นจำนวนจริงใดก็ได้ เพื่อหลีกเลี่ยงความคลุมเครือนี้ จึงถือว่า a≠1
ให้เราพิสูจน์ความได้เปรียบของเงื่อนไข a>0 ด้วย a=0 ตามนิยามของลอการิทึม เราจะมีความเท่าเทียมกันซึ่งเป็นไปได้ด้วย b=0 เท่านั้น แต่บันทึก 0 0 อาจเป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ เนื่องจากศูนย์ถึงกำลังใดๆ ที่ไม่ใช่ศูนย์จะเป็นศูนย์ เงื่อนไข a≠0 ช่วยให้เราสามารถหลีกเลี่ยงความคลุมเครือนี้ได้ และเมื่อก<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Поэтому и принимается условие a>0 .
สุดท้าย เงื่อนไข b>0 ตามมาจากความไม่เท่าเทียมกัน a>0 เนื่องจาก และค่าของกำลังที่มีฐานบวก a จะเป็นค่าบวกเสมอ
เพื่อสรุปประเด็นนี้ สมมติว่าคำจำกัดความที่ระบุของลอการิทึมทำให้คุณสามารถระบุค่าของลอการิทึมได้ทันที เมื่อตัวเลขที่อยู่ใต้เครื่องหมายลอการิทึมเป็นกำลังที่แน่นอนของฐาน จริงๆ แล้ว คำจำกัดความของลอการิทึมช่วยให้เราระบุได้ว่าถ้า b=a p แล้วลอการิทึมของจำนวน b ถึงฐาน a จะเท่ากับ p นั่นคือ บันทึกความเท่าเทียมกัน a a p =p เป็นจริง ตัวอย่างเช่น เรารู้ว่า 2 3 =8 จากนั้นให้บันทึก 2 8=3 เราจะพูดถึงเรื่องนี้เพิ่มเติมในบทความ
ลอการิทึมของตัวเลข b (b > 0) ถึงฐาน a (a > 0, a ≠ 1)– เลขชี้กำลังที่ต้องยกจำนวน a เพื่อให้ได้ b
ลอการิทึมฐาน 10 ของ b สามารถเขียนได้เป็น บันทึก(ข)และลอการิทึมฐาน e (ลอการิทึมธรรมชาติ) คือ จริง(ข).
มักใช้เมื่อแก้ปัญหาเกี่ยวกับลอการิทึม:
คุณสมบัติของลอการิทึม
มีสี่หลัก คุณสมบัติของลอการิทึม.
ให้ a > 0, a ≠ 1, x > 0 และ y > 0
คุณสมบัติ 1. ลอการิทึมของผลิตภัณฑ์
ลอการิทึมของผลิตภัณฑ์เท่ากับผลรวมของลอการิทึม:
บันทึก a (x ⋅ y) = บันทึก a x + บันทึก a y
คุณสมบัติ 2. ลอการิทึมของผลหาร
ลอการิทึมของผลหารเท่ากับผลต่างของลอการิทึม:
บันทึก a (x / y) = บันทึก a x – บันทึก a y
คุณสมบัติ 3. ลอการิทึมของกำลัง
ลอการิทึมของดีกรีเท่ากับผลคูณของกำลังและลอการิทึม:
ถ้าฐานของลอการิทึมอยู่ในองศา แสดงว่ามีการใช้สูตรอื่น:
คุณสมบัติ 4. ลอการิทึมของรูต
คุณสมบัตินี้สามารถหาได้จากคุณสมบัติของลอการิทึมของกำลัง เนื่องจากรากที่ n ของกำลังเท่ากับกำลัง 1/n:
สูตรการแปลงจากลอการิทึมในฐานหนึ่งไปเป็นลอการิทึมในอีกฐานหนึ่ง
สูตรนี้มักใช้เมื่อแก้งานต่างๆ เกี่ยวกับลอการิทึม:
กรณีพิเศษ:
การเปรียบเทียบลอการิทึม (อสมการ)
ขอให้เรามี 2 ฟังก์ชัน f(x) และ g(x) ภายใต้ลอการิทึมที่มีฐานเดียวกันและระหว่างนั้นมีเครื่องหมายอสมการ:
หากต้องการเปรียบเทียบ คุณต้องดูที่ฐานของลอการิทึม a ก่อน:
- ถ้า a > 0 แล้ว f(x) > g(x) > 0
- ถ้า 0< a < 1, то 0 < f(x) < g(x)
วิธีแก้ปัญหาลอการิทึม: ตัวอย่าง
ปัญหาเกี่ยวกับลอการิทึมรวมอยู่ในการสอบ Unified State ในวิชาคณิตศาสตร์สำหรับเกรด 11 ในงาน 5 และงาน 7 คุณสามารถค้นหางานพร้อมวิธีแก้ไขบนเว็บไซต์ของเราในส่วนที่เหมาะสม นอกจากนี้ งานที่มีลอการิทึมยังพบได้ในคลังงานทางคณิตศาสตร์อีกด้วย คุณสามารถค้นหาตัวอย่างทั้งหมดได้โดยการค้นหาเว็บไซต์
ลอการิทึมคืออะไร
ลอการิทึมถือเป็นหัวข้อที่ยากในหลักสูตรคณิตศาสตร์ของโรงเรียนมาโดยตลอด มีคำจำกัดความของลอการิทึมที่แตกต่างกันมากมาย แต่ด้วยเหตุผลบางประการ หนังสือเรียนส่วนใหญ่จึงใช้คำเหล่านี้ที่ซับซ้อนที่สุดและไม่ประสบความสำเร็จ
เราจะนิยามลอการิทึมอย่างเรียบง่ายและชัดเจน เมื่อต้องการทำเช่นนี้ เรามาสร้างตารางกัน:
ดังนั้นเราจึงมีพลังของทั้งสอง
ลอการิทึม - คุณสมบัติ สูตร วิธีการแก้
หากคุณนำตัวเลขมาจากบรรทัดล่างสุด คุณจะพบพลังที่คุณจะต้องยกสองขึ้นเพื่อให้ได้ตัวเลขนี้ได้อย่างง่ายดาย ตัวอย่างเช่น หากต้องการได้ 16 คุณต้องยกสองยกกำลังสี่ และเพื่อให้ได้ 64 คุณต้องยกสองยกกำลังหก ดังที่เห็นได้จากตาราง
และตอนนี้ - จริงๆ แล้ว คำจำกัดความของลอการิทึม:
ฐาน a ของอาร์กิวเมนต์ x คือกำลังที่ต้องยกจำนวน a เพื่อให้ได้จำนวน x
ชื่อ: log a x = b โดยที่ a คือฐาน x คืออาร์กิวเมนต์ b คือค่าลอการิทึมที่เท่ากับจริง
ตัวอย่างเช่น 2 3 = 8 ⇒log 2 8 = 3 (ลอการิทึมฐาน 2 ของ 8 คือ 3 เพราะ 2 3 = 8) ด้วยความสำเร็จเดียวกัน บันทึก 2 64 = 6 เนื่องจาก 2 6 = 64
การดำเนินการค้นหาลอการิทึมของตัวเลขไปยังฐานที่กำหนดเรียกว่า เรามาเพิ่มบรรทัดใหม่ให้กับตารางของเรา:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| บันทึก 2 2 = 1 | บันทึก 2 4 = 2 | บันทึก 2 8 = 3 | บันทึก 2 16 = 4 | บันทึก 2 32 = 5 | บันทึก 2 64 = 6 |
น่าเสียดายที่ไม่ใช่ทุกลอการิทึมจะคำนวณได้ง่ายนัก ตัวอย่างเช่น ลองค้นหาบันทึก 2 5 ตัวเลข 5 ไม่ได้อยู่ในตาราง แต่ตรรกะกำหนดว่าลอการิทึมจะอยู่ที่ไหนสักแห่งในช่วงเวลา เพราะ 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
ตัวเลขดังกล่าวเรียกว่าจำนวนอตรรกยะ: ตัวเลขที่อยู่หลังจุดทศนิยมสามารถเขียนได้ไม่จำกัด และจะไม่มีวันซ้ำกัน หากลอการิทึมกลายเป็นแบบไม่ลงตัว ก็ควรปล่อยไว้อย่างนั้นดีกว่า: log 2 5, log 3 8, log 5 100
สิ่งสำคัญคือต้องเข้าใจว่าลอการิทึมคือนิพจน์ที่มีตัวแปรสองตัว (ฐานและอาร์กิวเมนต์) ในตอนแรก หลายคนสับสนว่าอะไรเป็นพื้นฐานและข้อโต้แย้งอยู่ที่ไหน เพื่อหลีกเลี่ยงความเข้าใจผิดที่น่ารำคาญ เพียงแค่ดูภาพ:
ก่อนหน้าเราไม่มีอะไรมากไปกว่าคำจำกัดความของลอการิทึม จดจำ: ลอการิทึมคือกำลังซึ่งจะต้องสร้างฐานเพื่อให้ได้ข้อโต้แย้ง เป็นฐานที่ยกกำลังขึ้น - ในภาพเน้นด้วยสีแดง ปรากฎว่าฐานอยู่ด้านล่างเสมอ! ฉันบอกกฎที่ยอดเยี่ยมนี้แก่นักเรียนในบทเรียนแรก - และไม่มีความสับสนเกิดขึ้น
วิธีการนับลอการิทึม
เราได้ทราบคำจำกัดความแล้ว - สิ่งที่เหลืออยู่คือการเรียนรู้วิธีนับลอการิทึม เช่น กำจัดเครื่องหมาย "บันทึก" อันดับแรก เราสังเกตว่ามีข้อเท็จจริงสำคัญสองประการตามคำจำกัดความนี้:
- อาร์กิวเมนต์และฐานต้องมากกว่าศูนย์เสมอ สิ่งนี้ตามมาจากคำจำกัดความของระดับด้วยเลขชี้กำลังที่เป็นตรรกยะ ซึ่งคำจำกัดความของลอการิทึมจะลดลง
- ฐานจะต้องแตกต่างจากฐานหนึ่ง เนื่องจากระดับหนึ่งถึงระดับใดยังคงเป็นหนึ่ง ด้วยเหตุนี้ คำถามที่ว่า “คนๆ หนึ่งจะต้องเพิ่มพลังเท่าใดจึงจะได้สอง” จึงไม่มีความหมาย ไม่มีปริญญาขนาดนั้น!
ข้อจำกัดดังกล่าวเรียกว่า ภูมิภาค ค่าที่ยอมรับได้ (ODZ). ปรากฎว่า ODZ ของลอการิทึมมีลักษณะดังนี้: log a x = b ⇒x > 0, a > 0, a ≠ 1
โปรดทราบว่าไม่มีข้อจำกัดเกี่ยวกับจำนวน b (ค่าของลอการิทึม) ตัวอย่างเช่น ลอการิทึมอาจเป็นลบ: log 2 0.5 = −1 เพราะ 0.5 = 2 −1
อย่างไรก็ตาม ตอนนี้เรากำลังพิจารณาเฉพาะนิพจน์ตัวเลข โดยไม่จำเป็นต้องทราบ VA ของลอการิทึม ผู้เขียนปัญหาได้คำนึงถึงข้อจำกัดทั้งหมดแล้ว แต่เมื่อสมการลอการิทึมและอสมการเข้ามามีบทบาท ข้อกำหนด DL จะกลายเป็นข้อบังคับ ท้ายที่สุดแล้ว พื้นฐานและการโต้แย้งอาจมีโครงสร้างที่แข็งแกร่งมากซึ่งไม่จำเป็นต้องสอดคล้องกับข้อจำกัดข้างต้น
ทีนี้ลองมาพิจารณากัน โครงการทั่วไปการคำนวณลอการิทึม ประกอบด้วยสามขั้นตอน:
- เขียนฐาน a และอาร์กิวเมนต์ x เป็นกำลังโดยมีฐานขั้นต่ำที่เป็นไปได้มากกว่า 1 ระหว่างทางควรกำจัดทศนิยมออกไปจะดีกว่า
- แก้สมการของตัวแปร b: x = a b ;
- ผลลัพธ์หมายเลข b จะเป็นคำตอบ
แค่นั้นแหละ! หากลอการิทึมกลายเป็นจำนวนตรรกยะ สิ่งนี้จะมองเห็นได้ในขั้นตอนแรก ข้อกำหนดที่ว่าฐานต้องมากกว่าหนึ่งมีความสำคัญมาก ซึ่งจะช่วยลดโอกาสที่จะเกิดข้อผิดพลาดและทำให้การคำนวณง่ายขึ้นอย่างมาก เช่นเดียวกับเศษส่วนทศนิยม: หากคุณแปลงเป็นเศษส่วนธรรมดาทันที จะมีข้อผิดพลาดน้อยลงมาก
มาดูกันว่าโครงร่างนี้ทำงานอย่างไรโดยใช้ตัวอย่างเฉพาะ:
งาน. คำนวณลอการิทึม: บันทึก 5 25
- ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังของห้า: 5 = 5 1 ; 25 = 5 2 ;
- เราได้รับคำตอบ: 2.
มาสร้างและแก้สมการกัน:
บันทึก 5 25 = b ⇒ (5 1) b = 5 2 ⇒5 b = 5 2 ⇒ b = 2;
งาน. คำนวณลอการิทึม:
งาน. คำนวณลอการิทึม: บันทึก 4 64
- ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังสอง: 4 = 2 2 ; 64 = 2 6 ;
- มาสร้างและแก้สมการกัน:
บันทึก 4 64 = b ⇒(2 2) b = 2 6 ⇒2 2b = 2 6 ⇒2b = 6 ⇒ b = 3; - เราได้รับคำตอบ: 3.
งาน. คำนวณลอการิทึม: log 16 1
- ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังสอง: 16 = 2 4 ; 1 = 2 0 ;
- มาสร้างและแก้สมการกัน:
บันทึก 16 1 = b ⇒ (2 4) b = 2 0 ⇒2 4b = 2 0 ⇒4b = 0 ⇒ b = 0; - เราได้รับคำตอบ: 0.
งาน. คำนวณลอการิทึม: บันทึก 7 14
- ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังของเจ็ด: 7 = 7 1 ; 14 ไม่สามารถแสดงเป็นกำลังของ 7 ได้ เนื่องจาก 7 1< 14 < 7 2 ;
- จากย่อหน้าก่อนหน้า ตามมาว่าไม่นับลอการิทึม
- คำตอบคือไม่มีการเปลี่ยนแปลง: บันทึก 7 14
หมายเหตุเล็ก ๆ เกี่ยวกับตัวอย่างสุดท้าย คุณจะแน่ใจได้อย่างไรว่าตัวเลขนั้นไม่ใช่กำลังที่แน่นอนของอีกจำนวนหนึ่ง? ง่ายมาก - แค่แยกตัวประกอบเป็นปัจจัยเฉพาะ ถ้าการขยายตัวมีปัจจัยที่แตกต่างกันอย่างน้อยสองปัจจัย ตัวเลขจะไม่ใช่กำลังที่แน่นอน
งาน. ค้นหาว่าตัวเลขนั้นเป็นเลขยกกำลังที่แน่นอนหรือไม่: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 - องศาที่แน่นอน เพราะ มีตัวคูณเพียงตัวเดียวเท่านั้น
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - ไม่ใช่กำลังที่แน่นอน เนื่องจากมีปัจจัยสองประการ: 3 และ 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - ระดับที่แน่นอน;
35 = 7 · 5 - ไม่ใช่กำลังที่แน่นอนอีกครั้ง
14 = 7 · 2 - ไม่ใช่ระดับที่แน่นอนอีกครั้ง
โปรดสังเกตด้วยว่าจำนวนเฉพาะนั้นมักจะเป็นกำลังที่แน่นอนของตัวมันเองเสมอ
ลอการิทึมทศนิยม
ลอการิทึมบางตัวเป็นเรื่องธรรมดามากจนมีชื่อและสัญลักษณ์พิเศษ
ของอาร์กิวเมนต์ x คือลอการิทึมของฐาน 10 เช่น ยกกำลังที่ต้องยกเลข 10 เพื่อให้ได้เลข x ชื่อ: lg x.
ตัวอย่างเช่น บันทึก 10 = 1; แอลจี 100 = 2; lg 1,000 = 3 - ฯลฯ
จากนี้ไปเมื่อมีวลีเช่น “Find lg 0.01” ปรากฏในหนังสือเรียน โปรดทราบว่านี่ไม่ใช่การพิมพ์ผิด นี่คือลอการิทึมทศนิยม อย่างไรก็ตาม หากคุณไม่คุ้นเคยกับสัญกรณ์นี้ คุณสามารถเขียนใหม่ได้ตลอดเวลา:
บันทึก x = บันทึก 10 x
ทุกอย่างที่เป็นจริงสำหรับลอการิทึมธรรมดาก็เป็นจริงสำหรับลอการิทึมฐานสิบเช่นกัน
ลอการิทึมธรรมชาติ
มีลอการิทึมอื่นที่มีการกำหนดของตัวเอง ในบางแง่ มันสำคัญกว่าทศนิยมด้วยซ้ำ เรากำลังพูดถึงลอการิทึมธรรมชาติ
ของอาร์กิวเมนต์ x คือลอการิทึมของฐาน e เช่น เลขยกกำลังที่ต้องยกกำลัง e เพื่อให้ได้เลข x ชื่อ: ln x.
หลายคนจะถามว่า ตัวเลข e คืออะไร? นี่เป็นจำนวนอตรรกยะ ไม่สามารถหาค่าที่แน่นอนและจดบันทึกไว้ได้ ฉันจะให้เฉพาะตัวเลขแรกเท่านั้น:
อี = 2.718281828459…
เราจะไม่ลงรายละเอียดว่าหมายเลขนี้คืออะไรและเหตุใดจึงต้องมี เพียงจำไว้ว่า e เป็นฐานของลอการิทึมธรรมชาติ:
ln x = บันทึก อี x
ดังนั้น ln e = 1; ใน อี 2 = 2; ใน อี 16 = 16 - เป็นต้น ในทางกลับกัน ln 2 เป็นจำนวนอตรรกยะ โดยทั่วไป ลอการิทึมธรรมชาติของจำนวนตรรกยะใดๆ จะเป็นจำนวนตรรกยะ ยกเว้น อย่างหนึ่ง: ln 1 = 0
สำหรับลอการิทึมธรรมชาติ กฎทั้งหมดที่เป็นจริงสำหรับลอการิทึมสามัญนั้นใช้ได้
ดูเพิ่มเติมที่:
ลอการิทึม. คุณสมบัติของลอการิทึม (กำลังของลอการิทึม)
จะแสดงตัวเลขเป็นลอการิทึมได้อย่างไร?
เราใช้คำจำกัดความของลอการิทึม
ลอการิทึมเป็นเลขชี้กำลังที่ต้องยกฐานขึ้นเพื่อให้ได้ตัวเลขที่อยู่ใต้เครื่องหมายลอการิทึม
ดังนั้น ในการที่จะแทนจำนวน c ที่แน่นอนเป็นลอการิทึมของฐาน a คุณต้องใส่กำลังที่มีฐานเดียวกันกับฐานของลอการิทึมใต้เครื่องหมายลอการิทึม และเขียนตัวเลข c นี้เป็นเลขชี้กำลัง:
จำนวนใดๆ ก็ตามสามารถแสดงเป็นลอการิทึมได้อย่างแน่นอน - บวก, ลบ, จำนวนเต็ม, เศษส่วน, ตรรกยะ, อตรรกยะ:
![]()
เพื่อไม่ให้เกิดความสับสนระหว่าง a และ c ภายใต้สภาวะตึงเครียดของการทดสอบ คุณสามารถใช้กฎการท่องจำต่อไปนี้:
สิ่งที่อยู่ด้านล่างลงไป สิ่งที่อยู่ด้านบนก็ขึ้นไป
ตัวอย่างเช่น คุณต้องแสดงตัวเลข 2 เป็นลอการิทึมของฐาน 3
เรามีตัวเลขสองตัว - 2 และ 3 ตัวเลขเหล่านี้เป็นฐานและเลขชี้กำลังซึ่งเราจะเขียนไว้ใต้เครื่องหมายลอการิทึม ยังคงต้องพิจารณาว่าควรเขียนตัวเลขใดเหล่านี้ลงไปที่ฐานของระดับและตัวเลขใดขึ้นไปถึงเลขชี้กำลัง
ฐาน 3 ในสัญลักษณ์ลอการิทึมจะอยู่ด้านล่าง ซึ่งหมายความว่าเมื่อเราแทนสองเป็นลอการิทึมของฐาน 3 เราก็จะเขียน 3 ลงไปที่ฐานด้วย
2 สูงกว่าสาม และในสัญลักษณ์ของดีกรี 2 เราเขียนไว้เหนือทั้งสาม นั่นคือเป็นเลขชี้กำลัง:
ลอการิทึม ระดับรายการ
ลอการิทึม
ลอการิทึมจำนวนบวก ขขึ้นอยู่กับ ก, ที่ไหน ก > 0, ก ≠ 1เรียกว่าเลขยกกำลังที่ต้องยกจำนวนขึ้น กที่จะได้รับ ข.
ความหมายของลอการิทึมสามารถเขียนสั้น ๆ ได้ดังนี้:
ความเท่าเทียมกันนี้ใช้ได้สำหรับ ข > 0, ก > 0, ก ≠ 1.โดยปกติจะเรียกว่า เอกลักษณ์ลอการิทึม
การกระทำของการค้นหาลอการิทึมของตัวเลขเรียกว่า โดยลอการิทึม
คุณสมบัติของลอการิทึม:
ลอการิทึมของผลิตภัณฑ์:
ลอการิทึมของผลหาร:
การแทนที่ฐานลอการิทึม:
![]()
ลอการิทึมของดีกรี:
ลอการิทึมของราก:
![]()
ลอการิทึมพร้อมฐานกำลัง:
![]()
![]()
![]()
ลอการิทึมทศนิยมและลอการิทึมธรรมชาติ
ลอการิทึมทศนิยมตัวเลขเรียกลอการิทึมของตัวเลขนี้เป็นฐาน 10 แล้วเขียน lg ข
ลอการิทึมธรรมชาติตัวเลขนั้นเรียกว่าลอการิทึมของตัวเลขนั้นถึงฐาน จ, ที่ไหน จ- จำนวนอตรรกยะประมาณเท่ากับ 2.7 ในเวลาเดียวกันพวกเขาก็เขียน ln ข.
หมายเหตุอื่น ๆ เกี่ยวกับพีชคณิตและเรขาคณิต
คุณสมบัติพื้นฐานของลอการิทึม
คุณสมบัติพื้นฐานของลอการิทึม
ลอการิทึมก็เหมือนกับตัวเลขอื่นๆ ที่สามารถบวก ลบ และแปลงได้ในทุกวิถีทาง แต่เนื่องจากลอการิทึมไม่ใช่ตัวเลขธรรมดาเสียทีเดียว จึงมีกฎที่เรียกว่า คุณสมบัติหลัก.
คุณจำเป็นต้องรู้กฎเหล่านี้อย่างแน่นอน - ไม่ใช่ปัญหาลอการิทึมร้ายแรงแม้แต่ข้อเดียวที่ไม่สามารถแก้ไขได้หากไม่มีกฎเหล่านี้ นอกจากนี้ยังมีน้อยมาก - คุณสามารถเรียนรู้ทุกสิ่งได้ภายในวันเดียว มาเริ่มกันเลย
การบวกและการลบลอการิทึม
พิจารณาลอการิทึมสองตัวที่มีฐานเดียวกัน: บันทึก a x และบันทึก a y จากนั้นจึงสามารถบวกและลบได้ และ:
- บันทึก a x + บันทึก a y = บันทึก a (x y);
- log a x − log a y = log a (x: y)
ดังนั้น ผลรวมของลอการิทึมเท่ากับลอการิทึมของผลิตภัณฑ์ และผลต่างเท่ากับลอการิทึมของผลหาร โปรดทราบ: จุดสำคัญที่นี่ - บริเวณที่เหมือนกัน- หากเหตุผลแตกต่าง กฎเหล่านี้ใช้ไม่ได้!
สูตรเหล่านี้จะช่วยคุณคำนวณนิพจน์ลอการิทึมแม้ว่าจะไม่ได้พิจารณาแต่ละส่วนก็ตาม (ดูบทเรียน "ลอการิทึมคืออะไร") ดูตัวอย่างและดู:
ล็อก 6 4 + ล็อก 6 9
เนื่องจากลอการิทึมมีฐานเท่ากัน เราจึงใช้สูตรผลรวม:
บันทึก 6 4 + บันทึก 6 9 = บันทึก 6 (4 9) = บันทึก 6 36 = 2
งาน. ค้นหาค่าของนิพจน์: log 2 48 − log 2 3
ฐานเท่ากัน เราใช้สูตรผลต่าง:
บันทึก 2 48 - บันทึก 2 3 = บันทึก 2 (48: 3) = บันทึก 2 16 = 4
งาน. ค้นหาค่าของนิพจน์: log 3 135 − log 3 5
ฐานก็เหมือนกัน ดังนั้นเราจึงได้:
บันทึก 3 135 - บันทึก 3 5 = บันทึก 3 (135: 5) = บันทึก 3 27 = 3
อย่างที่คุณเห็น นิพจน์ดั้งเดิมประกอบด้วยลอการิทึมที่ "ไม่ดี" ซึ่งไม่ได้คำนวณแยกกัน แต่หลังจากการแปลงจะได้ตัวเลขปกติโดยสมบูรณ์ หลายคนถูกสร้างขึ้นจากข้อเท็จจริงนี้ การทดสอบ- ใช่ สำนวนที่เหมือนการทดสอบมีการนำเสนออย่างจริงจังทุกประการ (บางครั้งแทบไม่มีการเปลี่ยนแปลงใดๆ) ในการสอบ Unified State
แยกเลขชี้กำลังออกจากลอการิทึม
ตอนนี้เรามาทำให้งานซับซ้อนขึ้นเล็กน้อย จะเกิดอะไรขึ้นถ้าฐานหรืออาร์กิวเมนต์ของลอการิทึมเป็นกำลัง? จากนั้นสามารถนำเลขชี้กำลังของระดับนี้ออกจากเครื่องหมายลอการิทึมได้ตามกฎต่อไปนี้:
จะเห็นได้ง่ายว่ากฎข้อสุดท้ายเป็นไปตามสองข้อแรก แต่ยังไงก็ดีกว่าที่จะจำไว้ - ในบางกรณีมันจะลดจำนวนการคำนวณลงอย่างมาก
แน่นอนว่า กฎทั้งหมดนี้สมเหตุสมผลหากสังเกต ODZ ของลอการิทึม: a > 0, a ≠ 1, x > 0 และอีกอย่างหนึ่ง: เรียนรู้การใช้สูตรทั้งหมดไม่เพียงแต่จากซ้ายไปขวาเท่านั้น แต่ยังในทางกลับกันอีกด้วย , เช่น. คุณสามารถป้อนตัวเลขก่อนที่ลอการิทึมจะลงชื่อเข้าใช้ลอการิทึมได้
วิธีแก้ลอการิทึม
นี่คือสิ่งที่จำเป็นบ่อยที่สุด
งาน. ค้นหาค่าของนิพจน์: log 7 49 6 .
กำจัดระดับของการโต้แย้งโดยใช้สูตรแรก:
บันทึก 7 49 6 = 6 บันทึก 7 49 = 6 2 = 12
งาน. ค้นหาความหมายของสำนวน:
โปรดทราบว่าตัวส่วนประกอบด้วยลอการิทึม ฐานและอาร์กิวเมนต์เป็นกำลังที่แน่นอน: 16 = 2 4 ; 49 = 7 2. เรามี:
ฉันคิดว่าตัวอย่างสุดท้ายต้องมีการชี้แจง ลอการิทึมหายไปไหน? จนถึงวินาทีสุดท้ายที่เราทำงานกับตัวส่วนเท่านั้น เรานำเสนอฐานและอาร์กิวเมนต์ของลอการิทึมที่อยู่ตรงนั้นในรูปแบบของกำลังและนำเลขชี้กำลังออกมา - เราได้เศษส่วน "สามชั้น"
ทีนี้มาดูเศษส่วนหลักกัน ตัวเศษและส่วนมีตัวเลขเดียวกัน: log 2 7 เนื่องจากบันทึก 2 7 ≠ 0 เราสามารถลดเศษส่วนได้ - 2/4 จะยังคงอยู่ในตัวส่วน ตามกฎของเลขคณิตแล้วทั้งสี่สามารถโอนไปยังตัวเศษซึ่งเป็นสิ่งที่ทำเสร็จแล้ว ผลลัพธ์คือคำตอบ: 2.
การเปลี่ยนไปสู่รากฐานใหม่
เมื่อพูดถึงกฎสำหรับการบวกและการลบลอการิทึม ฉันเน้นย้ำเป็นพิเศษว่ากฎเหล่านี้ใช้ได้เฉพาะกับฐานเดียวกันเท่านั้น จะทำอย่างไรถ้าเหตุผลต่างกัน? จะเกิดอะไรขึ้นถ้าพวกมันไม่ใช่เลขยกกำลังที่เท่ากัน?
สูตรสำหรับการเปลี่ยนไปใช้รากฐานใหม่มาช่วยเหลือ ให้เรากำหนดพวกมันในรูปแบบของทฤษฎีบท:
ให้ลอการิทึมบันทึก a x ให้ได้ ดังนั้น สำหรับจำนวน c ใดๆ ที่ c > 0 และ c ≠ 1 ความเท่ากันจะเป็นจริง:
โดยเฉพาะอย่างยิ่ง ถ้าเราตั้งค่า c = x เราจะได้:
จากสูตรที่สองเป็นไปตามว่าสามารถสลับฐานและอาร์กิวเมนต์ของลอการิทึมได้ แต่ในกรณีนี้นิพจน์ทั้งหมดจะ "พลิกกลับ" เช่น ลอการิทึมจะปรากฏในตัวส่วน
สูตรเหล่านี้ไม่ค่อยพบในนิพจน์ตัวเลขทั่วไป มีความเป็นไปได้ที่จะประเมินว่าสะดวกเพียงใดเมื่อแก้สมการลอการิทึมและอสมการเท่านั้น
แต่มีปัญหาที่ไม่สามารถแก้ไขได้เลยนอกจากการย้ายฐานรากใหม่ ลองดูสองสามสิ่งเหล่านี้:
งาน. ค้นหาค่าของนิพจน์: log 5 16 log 2 25
โปรดทราบว่าอาร์กิวเมนต์ของลอการิทึมทั้งสองมีกำลังที่แน่นอน มาดูตัวบ่งชี้กันดีกว่า: log 5 16 = log 5 2 4 = 4log 5 2; บันทึก 2 25 = บันทึก 2 5 2 = 2 บันทึก 2 5;
ทีนี้ลอง "ย้อนกลับ" ลอการิทึมที่สอง:
เนื่องจากผลคูณไม่เปลี่ยนแปลงเมื่อจัดเรียงปัจจัยใหม่ เราจึงคูณสี่และสองอย่างใจเย็น จากนั้นจึงจัดการกับลอการิทึม
งาน. ค้นหาค่าของนิพจน์: log 9 100 lg 3
ฐานและอาร์กิวเมนต์ของลอการิทึมแรกคือกำลังที่แน่นอน มาเขียนสิ่งนี้และกำจัดตัวบ่งชี้:
ตอนนี้ กำจัดลอการิทึมทศนิยมโดยการย้ายไปยังฐานใหม่:
เอกลักษณ์ลอการิทึมพื้นฐาน
บ่อยครั้งในกระบวนการแก้ปัญหา จำเป็นต้องแสดงตัวเลขเป็นลอการิทึมของฐานที่กำหนด
ในกรณีนี้สูตรต่อไปนี้จะช่วยเรา:
ในกรณีแรก ตัวเลข n จะกลายเป็นเลขชี้กำลังในอาร์กิวเมนต์ จำนวน n สามารถเป็นอะไรก็ได้ เพราะมันเป็นเพียงค่าลอการิทึม
สูตรที่สองเป็นคำจำกัดความที่ถอดความจริงๆ นั่นคือสิ่งที่เรียกว่า: .
อันที่จริง จะเกิดอะไรขึ้นถ้าเลข b ยกกำลังจนเลข b ยกกำลังนี้ให้เลข a? ถูกต้อง: ผลลัพธ์คือเลข a เดียวกัน อ่านย่อหน้านี้อย่างละเอียดอีกครั้ง หลายๆ คนอาจติดอยู่กับเรื่องนี้
เช่นเดียวกับสูตรสำหรับการย้ายไปยังฐานใหม่ บางครั้งเอกลักษณ์ลอการิทึมพื้นฐานก็เป็นวิธีแก้ปัญหาเดียวที่เป็นไปได้
งาน. ค้นหาความหมายของสำนวน:
โปรดทราบว่าบันทึก 25 64 = บันทึก 5 8 - เราแค่เอากำลังสองจากฐานและอาร์กิวเมนต์ของลอการิทึม เมื่อคำนึงถึงกฎในการคูณกำลังด้วยฐานเดียวกัน เราได้รับ:
ถ้าใครไม่รู้ นี่คืองานจริงจากการสอบ Unified State :)
หน่วยลอการิทึมและศูนย์ลอการิทึม
โดยสรุป ฉันจะให้สองตัวตนที่แทบจะเรียกได้ว่าเป็นคุณสมบัติไม่ได้ - แต่เป็นผลสืบเนื่องมาจากคำจำกัดความของลอการิทึม สิ่งเหล่านี้มักเกิดปัญหาอยู่เสมอ และน่าประหลาดใจที่ยังสร้างปัญหาให้กับนักเรียน "ขั้นสูง" อีกด้วย
- บันทึก a = 1 คือ จำไว้ทุกครั้ง: ลอการิทึมของฐานใดๆ a ของฐานนั้นจะเท่ากับ 1
- บันทึก 1 = 0 คือ ฐาน a สามารถเป็นอะไรก็ได้ แต่ถ้าอาร์กิวเมนต์มีหนึ่งค่า ลอการิทึมจะเท่ากับศูนย์! เพราะ 0 = 1 เป็นผลโดยตรงจากคำจำกัดความ
นั่นคือคุณสมบัติทั้งหมด อย่าลืมฝึกฝนการนำไปปฏิบัติ! ดาวน์โหลดเอกสารสรุปตอนต้นบทเรียน พิมพ์ออกมา และแก้ไขปัญหา
ลอการิทึม จำนวนบวก N ถึงฐาน(ข> 0, ข 1 ) เรียกว่าเลขชี้กำลัง x ที่คุณต้องสร้าง b เพื่อรับ N .
สัญกรณ์ลอการิทึม:
รายการนี้เทียบเท่ากับสิ่งต่อไปนี้:ขx = ยังไม่มีข้อความ .
ตัวอย่าง: บันทึก 3 81 = 4 เนื่องจาก 3 4 = 81;
ล็อก 1/3 27 = – 3 เนื่องจาก (1/3) - 3 = 3 3 = 27
คำจำกัดความของลอการิทึมข้างต้นสามารถเขียนได้เป็นเอกลักษณ์:

คุณสมบัติพื้นฐานของลอการิทึม
1) บันทึก ข= 1 , เพราะ ข 1 = ข.
ข
2) บันทึก 1 = 0 , เพราะ ข 0 = 1 .
ข
3) ลอการิทึมของผลิตภัณฑ์เท่ากับผลรวมของลอการิทึมของปัจจัย:
บันทึก( เกี่ยวกับ) = บันทึก ก+ บันทึก ข.
4) ลอการิทึมของผลหารเท่ากับผลต่างระหว่างลอการิทึมของเงินปันผลและตัวหาร:
บันทึก( ก/ข) = บันทึก ก- บันทึก ข.
5) ลอการิทึมของกำลังเท่ากับผลคูณของเลขชี้กำลังและลอการิทึมของฐาน:
บันทึก (ข เค ) = เคบันทึก ข.
ผลที่ตามมาของทรัพย์สินนี้คือ:ลอการิทึมของราก เท่ากับลอการิทึมของจำนวนรากหารด้วยกำลังของราก:

6) ถ้าฐานของลอการิทึมเป็นองศา ก็จะเป็นค่านั้น ส่วนผกผันของเลขชี้กำลังสามารถนำออกจากเครื่องหมายบันทึกได้สัมผัส:

คุณสมบัติสองรายการสุดท้ายสามารถรวมกันเป็นหนึ่งเดียว:

7) สูตรโมดูลัสการเปลี่ยนผ่าน (เช่นจ - การเปลี่ยนผ่านจากฐานเดียวลอการิทึมไปยังฐานอื่น):

ในกรณีพิเศษเมื่อ ไม่มี=กเรามี:
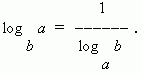
ลอการิทึมทศนิยม เรียกว่า ลอการิทึมฐาน 10. มีการกำหนดไว้แอลจี เช่น บันทึก 10 เอ็น = แอลจี เอ็น- ลอการิทึมของตัวเลข 10, 100, 1,000, ...พี ตัวเลขคือ 1, 2, 3, … ตามลำดับเหล่านั้น. มีแง่บวกมากมาย
หน่วย มีเลขศูนย์กี่ตัวในเลขลอการิทึมหลังหนึ่ง ลอการิทึมของตัวเลข 0.1, 0.01, 0.001, ...พี อาฟนา ตามลำดับ –1, –2, –3, …, เช่น มีค่าลบมากเท่ากับจำนวนศูนย์ที่อยู่หน้าค่าลอการิทึม ( การนับและจำนวนเต็มศูนย์- ลอการิทึม จำนวนอื่น ๆ มีส่วนที่เรียกว่าเศษส่วน แมนทิสซา- ทั้งหมดส่วนหนึ่งของลอการิทึมเรียกว่า ลักษณะเฉพาะ- เพื่อการใช้งานจริงลอการิทึมทศนิยมจะสะดวกที่สุด
ลอการิทึมธรรมชาติ
เรียกว่า ลอการิทึมฐาน
จ- มันถูกกำหนดไว้ฉันคือ บันทึก จเอ็น
=
ln เอ็น- ตัวเลข จมันไม่มีเหตุผลมูลค่าโดยประมาณ 2.718281828.มัน คือขีดจำกัดที่จำนวนมีแนวโน้ม(1 + 1
/
n)
n โดยเพิ่มขึ้นไม่จำกัดn(ซม. ขีดจำกัดอันมหัศจรรย์ครั้งแรก ).
อาจดูแปลก แต่ลอการิทึมธรรมชาติกลับกลายเป็นว่าสะดวกมากเมื่อดำเนินการประเภทต่าง ๆ ที่เกี่ยวข้องกับการวิเคราะห์ฟังก์ชันการคำนวณลอการิทึมเป็นฐานจดำเนินการได้เร็วกว่าเหตุผลอื่นมาก