Életünk során gyakran különböző közelítő értékekkel kell megküzdenünk. A hozzávetőleges számítások mindig számítások, némi hibával.

Az abszolút hiba fogalma

A hozzávetőleges érték abszolút hibája a pontos és a hozzávetőleges érték közötti különbség abszolút értéke.
Vagyis a pontos értékből ki kell vonni a hozzávetőleges értéket, és meg kell venni az eredő számot modulo. Ily módon abszolút hiba az érték mindig pozitív.

Az abszolút hiba kiszámítása

Mutassuk meg, hogy nézhet ki a gyakorlatban. Például van valamilyen értékű grafikonunk, legyen ez egy parabola: y \u003d x ^ 2.

A grafikon szerint egyes pontokon meghatározhatjuk a hozzávetőleges értéket. Például x \u003d 1,5 esetén az y értéke hozzávetőlegesen 2,2 (y2,2).

Az y \u003d x ^ 2 képlettel megtalálhatjuk a pontos értéket az x \u003d 1,5 y \u003d 2,25 pontban.

Most számítsuk ki méréseink abszolút hibáját. | 2,25-2,2 | \u003d | 0,05 | \u003d 0,05.

Az abszolút hiba 0,05. Ilyen esetekben azt mondják, hogy az érték kiszámítása 0,05 pontossággal történik.

Gyakran előfordul, hogy a pontos érték nem mindig található meg, ezért az abszolút hibát nem mindig lehet megtalálni.

Például, ha egy vonalzó segítségével kiszámítjuk a két pont távolságát, vagy egy szögmérő segítségével két egyenes közötti szög értékét, akkor hozzávetőleges értékeket kapunk. De a pontos értéket nem lehet kiszámítani. BAN BEN ebben az esetben, megadhatunk egy ilyen számot, amelynél nagyobb az abszolút hiba értéke nem lehet.

A vonalzóval ellátott példában ez 0,1 cm lesz, mivel a vonalzó beosztása 1 milliméter. A szögmérő példájában 1 fok, mert a szögmérő skálája minden fokozaton át van osztva. Így az abszolút hiba értéke az első esetben 0,1, a második esetben pedig 1.

Segítségre van szüksége a tanulmányaihoz?

Egyetlen mérés sem mentes a hibáktól, pontosabban a hibák nélküli mérés valószínűsége megközelíti a nullát. A hibák jellege és okai nagyon változatosak, és sok tényező befolyásolja őket (1.2. Ábra).

A befolyásoló tényezők általános jellemzői különböző szempontok szerint rendszerezhetők, például a felsorolt \u200b\u200btényezők hatása alapján (1.2. Ábra).

A mérési eredmények alapján a hibák három típusra oszthatók: szisztematikus, véletlenszerű és hiányzások.

Szisztematikus hibák, viszont előfordulásuk és megnyilvánulásuk jellege miatt csoportokra vannak osztva. Különböző módon kiküszöbölhetők, például módosítások bevezetésével.

ábra. 1.2

Véletlen hibák változó tényezők komplex halmaza okozza, általában ismeretlen és nehezen elemezhető. Hatásuk a mérési eredményre csökkenthető például ismételt mérésekkel, a valószínűségelmélet módszerével kapott eredmények további statisztikai feldolgozásával.

NAK NEK hiányzik tartalmazzák azokat a durva hibákat, amelyek a kísérleti körülmények hirtelen változásával merülnek fel. Ezek a pontatlanságok szintén véletlenszerű jellegűek, és azonosítás után meg kell őket szüntetni.

A mérési pontosságot a mérési hibák becsülik meg, amelyeket előfordulásuk jellege instrumentális és módszertani, valamint a számítási módszer szerint abszolútra, relatívra és csökkentettre osztja.

Hangszeres a hibát a mérőeszköz pontossági osztálya jellemzi, amelyet útlevelében szabványosított alap- és kiegészítő hibák formájában adnak meg.

Módszeres a hiba a módszerek és a mérőeszközök tökéletlenségéből adódik.

Abszolút a hiba a mért G u és a mennyiség valódi G értéke közötti különbség, amelyet a következő képlet határoz meg:

Δ \u003d ΔG \u003d G u -G

Vegye figyelembe, hogy a mennyiség megadja a mért mennyiség méretét.

Relatív a hibát az egyenlőségből találjuk

δ \u003d ± ΔG / G u 100%

Az adott a hibát a képlet (a mérőeszköz pontossági osztálya) számítja ki

δ \u003d ± ΔG / G norm 100%

ahol G norma a mért érték normalizáló értéke. Ez egyenlő:

a) az eszköz skálájának végső értéke, ha a nulla jel a skála szélén vagy azon kívül található;

b) a skála végértékeinek összege a jelek figyelembevétele nélkül, ha a nulla jel a skálán belül helyezkedik el;

c) a skála hossza, ha a skála egyenetlen.

Az eszköz pontossági osztálya az ellenőrzéskor jön létre, és a képletek által kiszámított szabványosított hiba

γ \u003d ± ΔG / G norma 100%, haΔG m \u003d konst

ahol ΔG m az eszköz lehető legnagyobb abszolút hibája;

G k - az eszköz mérési határának végső értéke; с és d olyan együtthatók, amelyek figyelembe veszik a készülék mérési mechanizmusának tervezési paramétereit és tulajdonságait.

Például egy állandó relatív hibával rendelkező voltmérő esetében az egyenlőség

8 m \u003d ± c

A relatív és csökkentett hibákat a következő függőségek kapcsolják össze:

a) a csökkentett hiba bármely értékére

δ \u003d ± γ G norm / G u

b) a legnagyobb csökkentett hiba esetén

δ \u003d ± γ m G norm / G u

Ezekből az arányokból az következik, hogy például feszültségmérővel történő méréskor egy áramkörben ugyanazon feszültségérték mellett minél alacsonyabb a mért feszültség, annál nagyobb a relatív hiba. És ha ezt a voltmérőt helytelenül választják, akkor a relatív hiba arányos lehet az értékkelG n ami érvénytelen. Vegye figyelembe, hogy a megoldandó problémák terminológiájának megfelelően, például a G \u003d U feszültség mérésekor, a C \u003d I áram mérésekor a hibák kiszámításának képleteiben szereplő betűjelzéseket fel kell cserélni a megfelelő szimbólumokra.

1.1. Példa Voltmérővel, amelynek értéke γ m \u003d 1,0%, U n \u003d G normák, G k \u003d 450 V, mérjük meg az U u feszültséget, egyenlő 10 V-val. Becsüljük meg a mérési hibákat.

Döntés.

Válasz. A mérési hiba 45%. Ilyen hiba esetén a mért feszültség nem tekinthető megbízhatónak.

Mikor fogyatékosságok eszköz (voltmérő) kiválasztása esetén a képlettel kiszámított korrekcióval a módszertani hiba figyelembe vehető

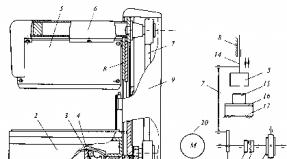
1.2. Példa Számítsa ki az áramkör feszültségének mérésekor a V7-26 voltmérő abszolút hibáját egyenáram... A voltmérő pontossági osztályát a maximálisan csökkentett hiba határozza meg: γ m \u003d ± 2,5%. A munkában használt voltmérő skála határértéke U norma \u003d 30 V.

Döntés.Az abszolút hibát a jól ismert képletekkel számolják:

(mivel a csökkentett hibát definíció szerint a képlet fejezi ki , akkor innen megtalálja az abszolút hibát:

Válasz. ΔU \u003d ± 0,75 V.

Az eredmények feldolgozása és a kerekítési szabályok fontos lépések a mérési folyamatban. A közelítő számítások elmélete lehetővé teszi az adatok pontosságának ismeretében az eredmények pontosságának becslését még a műveletek végrehajtása előtt: válassza ki az adatokat a megfelelő pontossággal, amely elegendő az eredmény szükséges pontosságának biztosításához, de nem túl magas ahhoz, hogy a számológépet megóvja a haszontalan számításoktól; racionalizálja magát a számítási folyamatot, megszabadítva azoktól a számításoktól, amelyek nem befolyásolják a pontos számokat és eredményeket.

Az eredmények feldolgozásakor kerekítési szabályokat alkalmaznak.

• 1. szabály Ha az eldobott számjegyek közül az első nagyobb, mint öt, akkor az utolsó tárolt számjegy eggyel növekszik.

• 2. szabály Ha az eldobott számjegyek közül az első kevesebb, mint öt, akkor nem történik növelés.

• 3. szabály Ha az eldobott számjegy öt, és nincs mögötte jelentős számjegy, akkor a kerekítést a legközelebbi páros számra, azaz az utolsó tárolt számjegy változatlan marad, ha páros, és növekszik, ha nem páros.

Ha az ötös szám mögött jelentős számjegyek vannak, akkor a kerekítés a 2. szabály szerint történik.

A 3. szabály alkalmazása egy szám kerekítésére nem növeli a kerekítés pontosságát. De sok kerekítéssel a felesleges számok kb. Olyan gyakran jelennek meg, ahányszor nem elég. A kölcsönös hibajavítás biztosítja a legpontosabb eredményt.

Olyan számot hívunk, amely nyilván meghaladja az abszolút hibát (vagy a legrosszabb esetben megegyezik vele) korlátozza az abszolút hibát.

A hibahatár nem egészen határozott. Minden hozzávetőleges számhoz meg kell ismerni a maximális hibáját (abszolút vagy relatív).

Ha nincs közvetlenül feltüntetve, akkor értendő, hogy a maximális abszolút hiba az utolsó írott rang egységének a fele. Tehát, ha hozzávetőlegesen 4,78-as számot adunk meg a maximális hiba megjelölése nélkül, akkor feltételezzük, hogy a maximális abszolút hiba 0,005. E megállapodás eredményeként mindig meg lehet tenni anélkül, hogy megadnánk az 1-3. Szabályok szerint kerekített szám maximális hibáját, vagyis ha a hozzávetőleges számot α betűvel jelöljük, akkor

Ahol Δn a végső abszolút hiba; és δ n a korlátozó relatív hiba.

Ezenkívül az eredmények feldolgozása során szabályok a hiba megtalálásához összeg, különbség, szorzat és hányados.

• 1. szabály Az összeg korlátozó abszolút hibája megegyezik az egyes feltételek korlátozó abszolút hibáinak összegével, de a kifejezések jelentős számú hibájával általában a hibák kölcsönös kompenzációja következik be, ezért az összeg valódi hibája csak kivételes esetekben esik egybe a korlátozó hibával, vagy közel áll hozzá.

• 2. szabály A különbség korlátozó abszolút hibája megegyezik a csökkentett vagy kivont korlátozó abszolút hibáinak összegével.

Korlátozó relatív hiba könnyű megtalálni a maximális abszolút hiba kiszámításával.

• 3. szabály Az összeg korlátozó relatív hibája (de nem a különbség) a kifejezések relatív hibái közül a legkisebb és a legnagyobb között van.

Ha az összes kifejezésnek ugyanaz a marginális relatív hibája, akkor az összegnek ugyanaz a marginális relatív hibája. Más szavakkal, ebben az esetben az összeg pontossága (százalékban kifejezve) nem alacsonyabb a feltételek pontosságánál.

Az összeggel ellentétben a hozzávetőleges számok közötti különbség kevésbé pontos lehet, mint a kivont és a kivont szám. A pontosságvesztés különösen akkor nagy, ha a kivont és a kivont kevés különbözik egymástól.

• 4. szabály A termék relatív relatív hibája megközelítőleg megegyezik a tényezők korlátozó relatív hibáinak összegével: δ \u003d δ 1 + δ 2, vagy pontosabban δ \u003d δ 1 + δ 2 + δ 1 δ 2, ahol δ a termék relatív hibája, δ 1 δ 2 a relatív hiba tényezők.

Megjegyzések:

1. Ha a hozzávetőleges számokat megszorozzuk ugyanannyi jelentős számjeggyel, akkor ugyanannyi jelentős számjegyet kell tárolni a termékben. A tárolt számok közül az utolsó nem lesz teljesen megbízható.

2. Ha egyes tényezők számszerűbb számjegyűek, mint mások, akkor az első szorzása előtt le kell kerekíteni, megadva annyi számjegyet, ahány legkevésbé pontos, vagy még egyet (tartalékként), felesleges további számjegyeket menteni.

3. Ha szükséges, hogy két szám szorzatának előre megadható legyen egy teljesen megbízható száma, akkor mindegyik tényezőnél a pontos (számítással vagy számítással kapott) számjegyek számának még egynek kell lennie. Ha a tényezők száma több mint kettő és kevesebb, mint tíz, akkor mindegyik tényezőnél a teljes garancia pontos számjegyeinek számának kettővel többnek kell lennie, mint a pontos számok előírt száma. A gyakorlatban elég, ha csak egy extra számot veszünk.

• 5. szabály A hányados korlátozó relatív hibája megközelítőleg megegyezik az osztalék és az osztó korlátozó relatív hibáinak összegével. A korlátozó relatív hiba pontos értéke mindig meghaladja a hozzávetőleges értéket. A túllépés százaléka megközelítőleg megegyezik az osztó maximális relatív hibájával.

1.3. Példa Keresse meg a 2.81: 0.571 hányados maximális abszolút hibáját.

Döntés.Az osztalék korlátozó relatív hibája 0,005: 2,81 \u003d 0,2%; osztó - 0,005: 0,571 \u003d 0,1%; magán - 0,2% + 0,1% \u003d 0,3%. A hányados korlátozó abszolút hibája körülbelül 2,81: 0,571 0,0030 \u003d 0,015

Ez azt jelenti, hogy a 2.81: 0.571 \u003d 4.92 hányadosban a harmadik szignifikáns adat nem megbízható.

Válasz.0,015.

1.4. Példa Számítsa ki az áramkör szerint csatlakoztatott voltmérő leolvasásainak relatív hibáját (1.3. Ábra), amelyet akkor kapunk, ha feltételezzük, hogy a voltmérőnek végtelen nagy az ellenállása és nem torzítja a mért áramkört. Besorolja a mérési bizonytalanságot ehhez a feladathoz.

ábra. 1.3

Döntés.Jelöljük egy valódi voltmérő leolvasását az AND-n keresztül, és a végtelen nagy ellenállású voltmérőt az AND-n keresztül. Viszonylagos hiba keresése

vegye észre, hogy

akkor megkapjuk

Mivel R AND \u003e\u003e R és R\u003e r, az utolsó egyenlőség nevezőjében lévő frakció jóval kevesebb, mint egy. Ezért használhatja a hozzávetőleges képletet érvényes λ≤1 bármely α esetén. Feltéve, hogy ebben a képletben α \u003d -1 és λ \u003d rR (r + R) -1 R AND -1, akkor δ ≈ rR / (r + R) R AND-t kapunk.

Minél nagyobb a voltmérő ellenállása az áramkör külső ellenállásához képest, annál kisebb a hiba. De az R feltétel<

Válasz.Szisztematikus módszertani hiba.

1.5. Példa Az egyenáramú áramkörbe a következő eszközök tartoznak (1.4. Ábra): A - M 330 típusú ampermérő, K A \u003d 1,5 pontossági osztályú, I k \u003d 20 A mérési határértékkel; А 1 - М 366 típusú ampermérő, К А1 \u003d 1,0 pontossági osztály, I к1 \u003d 7,5 A. mérési határértékkel , 0A. és I 1 \u003d 6,0A. Besorolás dimenzió.

ábra. 1.4

Döntés.Az I 2 áramot az eszköz leolvasásai alapján határozzuk meg (hibáik figyelembevétele nélkül): I 2 \u003d I-I 1 \u003d 8,0-6,0 \u003d 2,0 A.

Keressük meg az A és A 1 ampermérők abszolút hibáit

A esetében megvan az egyenlőség ampermérőhöz

Keressük meg az abszolút hibamodulok összegét:

Ezért a lehető legnagyobb és ugyanaz az érték ennek az értéknek a töredékeiben kifejezve 1. 10 3 - egy eszközhöz; 2 · 10 3 - egy másik eszközhöz. Ezen eszközök közül melyik lesz a legpontosabb?

Döntés.Az eszköz pontosságát a hibára fordított érték jellemzi (minél pontosabb az eszköz, annál kisebb a hiba), azaz az első eszköznél 1 / (1. 10 3) \u003d 1000, a másodiknál \u200b\u200b- 1 / (2. 10 3) \u003d 500. Vegye figyelembe, hogy 1000\u003e 500. Ezért az első eszköz kétszer pontosabb, mint a második.

Hasonló következtetésre lehet jutni a hibák megfelelőségének ellenőrzésével: 2. 10 3/1. 10 3 \u003d 2.

Válasz.Az első eszköz kétszer pontosabb, mint a második.

1.6. Példa Keresse meg a készülék hozzávetőleges mérésének összegét. Keresse meg a helyes karakterek számát: 0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667 + 0,0625 + 0,0588+ 0,0556 + 0,0526.

Döntés.Az összes mérési eredmény összeadásával 0,6187-et kapunk. Az összeg maximális maximális hibája 0,00005 9 \u003d 0,00045. Ez azt jelenti, hogy legfeljebb 5 egységnyi hiba lehetséges az összeg utolsó negyedik számjegyében. Ezért az összeget harmadik tizedesjegyig kerekítjük, azaz ezrelék, 0,619-et kapunk - ennek eredményeként minden jel helyes.

Válasz.0,619. A helyes karakterek száma három tizedesjegy.

Közvetlen mérésekkel

1. Mérjen meg egyszer két feszültséget egy voltmérőn U 1 \u003d 10 V, U 2 \u003d 200 V. A voltmérő a következő jellemzőkkel rendelkezik: d cl pontossági osztály t \u003d 0,2, U max \u003d 300 V.

Határozzuk meg ezen mérések abszolút és relatív hibáit.

Mivel mindkét mérést ugyanazon az eszközön végezték, akkor D U 1 \u003d D U 2 és a (B.4) képlettel számítják

A meghatározás szerint a relatív hibák U 1 és U 2 egyenlő

ε 1 \u003d 0,6 ∙ V / 10 V \u003d 0,06 \u003d 6%,

ε 2 \u003d 0,6 ∙ V / 200 V \u003d 0,003 \u003d 0,3%.

Az ε 1 és ε 2 adott számítási eredményei alapján látható, hogy ε 1 sokkal nagyobb, mint ε 2.

Ezért a szabály: olyan mérési határértékkel rendelkező készüléket kell választania, hogy az értékek a skála utolsó harmadában legyenek.

2. Mérjen meg valamilyen értéket sokszor, vagyis termeljen n ennek a mennyiségnek az egyedi mérése A x 1 , A x 2 ,..., A x 3 .

Ezután az abszolút hiba kiszámításához a következő műveleteket hajtják végre:

1) a (B.5) képlet alapján határozza meg a számtani középértéket ÉS 0 mért érték;

2) kiszámítja az egyes mérések eltéréseinek négyzetének összegét a talált számtani átlagtól, és a (B.6) képlet szerint meghatározza a négyzet alaptörvény hibát, amely egy adott érték abszolút hibáját jellemzi többszörös közvetlen méréssel egy bizonyos értéken;

3) az ε relatív hibát a (B.2) képlettel számoljuk.

Az abszolút és a relatív hiba kiszámítása

Közvetett mérés

A közvetett mérések hibáinak kiszámítása bonyolultabb feladat, mivel ebben az esetben a keresett érték más segédmennyiségek függvénye, amelyek mérésével együtt hibák jelentkeznek. Méréskor a véletlen hibák - a kihagyásoktól eltekintve - nagyon kicsiek a mért értékhez képest. Olyan kicsiek, hogy a második és a magasabb fokú hiba meghaladja a mérési pontosságot, és elhanyagolható. A hibaképlet megszerzéséhez szükséges hibák aprósága miatt
a közvetetten mért mennyiségek a differenciálszámítás módszereit alkalmazzák. Egy mennyiség közvetett mérése során, amikor a keresett bizonyos matematikai függőséghez tartozó mennyiségeket közvetlenül mérik, kényelmesebb először meghatározni a relatív hibát, és már
számítsa ki az abszolút mérési hibát a talált relatív hiba felhasználásával.

A differenciálszámítás biztosítja a legegyszerűbb módszert a közvetett mérés relatív hibájának meghatározására.

Legyen a keresett érték ÉS funkcionálisan több független, közvetlenül mért mennyiséghez kapcsolódik x 1 ,
x 2 , ..., x k, azaz

A= f(x 1 , x 2 , ..., x k).

Az érték relatív hibájának meghatározásához ÉS az egyenlőség mindkét oldalának természetes logaritmusát vesszük

ln A\u003d ln f(x 1 , x 2 , ..., x k).

Ezután kiszámítjuk a függvény természetes logaritmusának különbségét
A= f(x 1 ,x 2 , ..., x k),

dln A\u003d dln f(x 1 , x 2 , ..., x k)

A kapott kifejezésben minden lehetséges algebrai átalakítást és egyszerűsítést végrehajtunk. Ezt követően a d differenciálok összes szimbólumát a D hiba szimbólumai helyettesítik, és a független változók differenciáljai előtti negatív előjeleket pozitívakkal helyettesítik, vagyis az összes hiba hozzáadásakor a legkedvezőtlenebb esetet veszik fel. Ebben az esetben kiszámítják az eredmény maximális hibáját.

A fentiekre tekintettel

de ε \u003d D ÉS / ÉS

Ez a kifejezés az érték relatív hibájának képlete ÉS közvetett mérésekkel meghatározza a kívánt érték relatív hibáját a mért értékek relatív hibáin keresztül. Miután kiszámította a relatív hibát a (B.11) képlet szerint,
határozza meg az érték abszolút hibáját ÉS mint a kiszámított érték relatív hibájának szorzata ÉS azaz

D ÉS = ε ÉS, (12-KOR)

ahol az ε dimenzió nélküli számként van kifejezve.

Tehát a közvetetten mért érték relatív és abszolút hibáit a következő sorrendben kell kiszámítani:

1) a képletet vesszük, amely szerint kiszámítjuk a szükséges értéket (számítási képlet);

2) a számítási képlet mindkét részének természetes logaritmusát vesszük fel;

3) kiszámítja a kívánt érték természetes logaritmusának teljes különbségét;

4) az eredményül kapott kifejezésben minden lehetséges algebrai transzformáció és egyszerűsítés megtörténik;

5) a d differenciálok szimbólumát a D hiba szimbólumával helyettesítjük, míg a független változók differenciáljai előtti összes negatív előjelet pozitívra cseréljük (a relatív hiba nagysága maximális lesz), és megkapjuk a relatív hiba képletét;

6) kiszámítják a mért érték relatív hibáját;

7) a kiszámított relatív hiba szerint a közvetett mérés abszolút hibáját a (B.12) képlet segítségével számoljuk ki.

Vegyünk néhány példát a közvetett mérések relatív és abszolút hibáinak kiszámítására.

1. A keresett érték ÉS közvetlenül mérhető mennyiségekkel kapcsolatos x, nál nél, z hányados

ahol a és b - állandó értékek.

2. Vegyük a kifejezés természetes logaritmusát (B.13)

3. Számítsa ki a szükséges mennyiség természetes logaritmusának teljes különbségét ÉS, vagyis megkülönböztetünk (B.13)

4. Átalakításokat hajtunk végre. Tekintettel arra, hogy d és \u003d 0, mivel és\u003d const, cos nál nél/ bűn y \u003d ctg y, kapunk:

5. Cserélje ki a differenciálmű szimbólumait a hibaszimbólumokra, és a differenciálmű előtti mínuszjelet a pluszjelre

6. Kiszámoljuk a mért érték relatív hibáját.

7. A kiszámított relatív hiba szerint a közvetett mérés abszolút hibáját a (B.12) képlettel számoljuk, azaz

A higany spektrális vonalának sárga hullámhosszát diffrakciós rács segítségével határozzuk meg (a sárga hullámhossz relatív és abszolút hibáinak kiszámításához az elfogadott szekvenciát használjuk).

1. A sárga szín hullámhosszát ebben az esetben a következő képlet határozza meg:

ahol TÓL TŐL - a diffrakciós rács állandója (közvetetten mért érték); φ W a sárga vonal diffrakciós szöge a spektrum adott sorrendjében (közvetlenül mért érték); K g - a spektrum sorrendje, amelyben a megfigyelést végezték.

A diffrakciós rácsállandó a következő képlettel számítható

ahol K h - a zöld vonal spektrumának sorrendje; λ s - ismert zöld hullámhossz (λ s - állandó); φ z a zöld vonal diffrakciós szöge a spektrum adott sorrendjében (közvetlenül mért érték).

Ezután, figyelembe véve a kifejezést (B.15)

(B.16)

ahol K h, K g - megfigyelhetőek, amelyeket állandónak tekintenek; φ s, φ w - vannak
közvetlenül mért értékek.

Kifejezés (B.16) - a sárga hullámhossz kiszámított képlete, diffrakciós rács alkalmazásával meghatározva.

4.d K h \u003d 0; d K w \u003d 0; dλ s \u003d 0, mivel K h, K g és λ z konstansok;

Akkor

5. (B.17)

ahol Dφ W, Dφ W a sárga diffrakciós szögének abszolút hibája
és zöld spektrum vonalak.

6. Számítsa ki a sárga hullámhossz relatív hibáját!

7. Kiszámoljuk a sárga hullámhossz abszolút hibáját:

Dλ w \u003d ελ w.

Abszolút és relatív hiba

A hibák elméletének elemei

Pontos és hozzávetőleges számok

A szám pontossága általában nem kétséges, ha egész adatértékekről van szó (2 ceruza, 100 fa). Azonban a legtöbb esetben, amikor egy szám pontos értékét nem lehet megadni (például objektum vonalzóval történő mérésekor, készülékből származó eredmények vételével stb.), Hozzávetőleges adatokkal van dolgunk.

A hozzávetőleges érték az a szám, amely kissé eltér a pontos értéktől és helyettesíti a számításokban. A szám hozzávetőleges értéke és pontos értéke közötti különbség mértékét az jellemzi hiba .

A következő fő hibaforrásokat különböztetjük meg:

1. Hibák a probléma kimutatásábanegy valós jelenség matematikai szempontból történő hozzávetőleges leírása eredményeként keletkezik.

2. Módszerhibákkapcsolódik a probléma megoldásának nehézségéhez vagy lehetetlenségéhez és annak helyettesítéséhez hasonlóval, hogy ismert és hozzáférhető megoldási módszert lehessen alkalmazni, és a kívánthoz közeli eredményt érjünk el.

3. Végzetes hibáka kezdeti adatok hozzávetőleges értékeihez társítva és a hozzávetőleges számokra vonatkozó számítások elvégzése miatt.

4. Kerekítési hibák, összefüggésben a kiindulási adatok, a számítási eszközök alkalmazásával kapott közbenső és végső eredmények értékeinek kerekítésével.

Abszolút és relatív hiba

A hibák elszámolása fontos szempont a numerikus módszerek alkalmazásában, mivel a hiba a teljes probléma megoldásának végeredményében minden típusú hiba kölcsönhatásának eredménye. Ezért a hibaelmélet egyik fő feladata az eredmény pontosságának megbecsülése a kezdeti adatok pontossága alapján.

Ha pontos szám és hozzávetőleges értéke, akkor a hozzávetőleges érték hibája (hibája) az érték közelsége a pontos értékéhez.

A hiba legegyszerűbb kvantitatív mértéke az abszolút hiba, amelyet úgy definiálunk

(1.1.2-1)

Amint az az 1.1.2-1 képletből látható, az abszolút hibának ugyanazok a mértékegységei vannak, mint az értéknek. Ezért az abszolút hiba nagysága szerint korántsem mindig lehet helyes következtetést levonni a közelítés minőségéről. Például, ha , és a gép részleteiről beszélünk, a mérések nagyon durvaak, és ha körülbelül akkorák, mint az edény, akkor nagyon pontosak. Ezzel kapcsolatban bevezették a relatív hiba fogalmát, amelyben az abszolút hiba értéke a hozzávetőleges érték modulusához kapcsolódik ( ).

(1.1.2-2)

A relatív hibák használata különösen azért kényelmes, mert nem függenek a mennyiségek és az adategységek skálájától. A relatív hibát frakciókban vagy százalékokban mérjük. Tehát például, ha

,és akkor , és ha és ,

így aztán .

A függvény hibájának számszerűsítéséhez ismernie kell a műveletek hibájának kiszámításához szükséges alapvető szabályokat:

· számok összeadásakor és kivonásakor a számok abszolút hibái összeadódnak

· számok szorzásakor és osztásakor relatív hibáik összeadódnak

· amikor hozzávetőleges szám hatványára emelik relatív hibáját megszorozzuk a kitevõvel

1.1.2-1. Példa Adott egy függvény: ... Keresse meg az érték abszolút és relatív hibáját (hiba a számtani műveletek végrehajtásának eredményében), ha az értékek ismertek, és 1 pontos szám, hibája pedig nulla.

Miután meghatározta a relatív hiba értékét, megtalálja az abszolút hiba értékét, as , ahol az értéket a képlettel számoljuk hozzá közelítő értékekhez

Mivel a mennyiség pontos értéke általában ismeretlen, a számítás és a fenti képletek alapján lehetetlen. Ezért a gyakorlatban értékelik az űrlap korlátozó hibáit:

(1.1.2-3)

ahol és - ismert értékek, amelyek az abszolút és relatív hibák felső határai, különben hívják őket - a korlátozó abszolút és a korlátozó relatív hibák. Így a pontos érték a következőkön belül található:

Ha az érték akkor ismert , és ha a mennyiség akkor

Tegyük fel, hogy ezek sorozatát futtatjuk n azonos mennyiség mérése x... Véletlen hibák, egyedi értékek miatt x 1 , x 2 , x 3, x n nem azonosak, és a kívánt érték legjobb értékeként az összes mért érték számtani összegével megegyező számtani átlagot választjuk a mérések számával:

... (A.1)

ahol å az összeg jele, én - mérési szám, n - a mérések száma.

Tehát, - az igazihoz legközelebb eső érték. Senki sem tudja az igazi jelentést. Csak a D intervallumot számíthatja ki x ahol a valódi érték bizonyos fokú valószínűséggel megtalálható R... Ezt az intervallumot hívjuk megbízhatósági intervallum... Meghívjuk annak valószínűségét, amellyel a valódi érték beleesik megbízhatósági szint vagy megbízhatósági együttható(mivel a megbízhatósági szint ismerete lehetővé teszi, hogy megbecsüljük a kapott eredmény megbízhatóságának mértékét). A megbízhatósági intervallum kiszámításakor a szükséges megbízhatósági fokot előre meghatározzuk. A gyakorlati igények határozzák meg (például szigorúbb követelményeket támasztanak a repülőgép motorrészeivel szemben, mint a hajó motorjaival szemben). Nyilvánvaló, hogy a nagyobb megbízhatóság érdekében növelni kell a mérések számát és pontosságát.

Tekintettel arra, hogy az egyes mérések véletlenszerű hibái betartják a valószínűségi törvényeket, a matematikai statisztika és a valószínűségelmélet módszerei lehetővé teszik az aritmetikai átlag gyökér-négyzet hibájának kiszámítását Dx sl. Írjuk le bizonyítás nélkül a számítási képletet! Dx sl kis számú méréssel ( n < 30).

A képletet Student-képletnek hívjuk:

, (A.2)

ahol t n, p - Student-együttható, a mérések számától függően n és a bizalom szintje r.

A hallgatói együtthatót az alábbi táblázat tartalmazza, miután a gyakorlati igények alapján (ahogy fent említettük) korábban meghatároztuk az értékeket n és r.

A laboratóriumi munka eredményeinek feldolgozásakor elég 3-5 mérést végrehajtani, és a megbízhatósági szintet 0,68-nak vesszük.

De előfordul, hogy több méréssel ugyanazokat az értékeket kapjuk x... Például a huzalátmérőt ötször mértük, és ugyanezt az értéket ötször kaptuk meg. Tehát ez egyáltalán nem jelenti azt, hogy nincs hiba. Ez csak azt jelenti, hogy az egyes mérések véletlenszerű hibája kisebb pontosság d eszköz, amelyet szintén hívnak hangszeres,vagy hangszeres, hiba. A d műszer műszeres hibáját a műszer útlevelében feltüntetett, vagy magán a műszeren feltüntetett pontossági osztály határozza meg. Néha úgy tekintik, hogy megegyezik az eszköz osztási értékével (az eszköz osztási értéke a legkisebb osztás értéke), vagy a felezési érték felével (ha a készülék osztási értékének hozzávetőlegesen a fele szemmel meghatározható).

Mivel mindegyik érték x d hibával kaptam, akkor a teljes konfidencia intervallumot Dx, vagy az abszolút mérési hibát a következő képlettel számítják ki:

... (A.3)

Vegye figyelembe, hogy ha az (A.3) képletben az egyik mennyiség legalább háromszor nagyobb, mint a másik, akkor a kisebbet elhanyagoljuk.

Az abszolút hiba önmagában nem tükrözi a mérések minőségét. Például pusztán információk alapján az abszolút hiba 0,002 m², nem lehet megítélni, hogy egy adott mérést milyen jól hajtottak végre. A végrehajtott mérések minőségéről képet ad relatív hiba e, egyenlő az abszolút hiba és a mért érték átlagos értékének arányával. A relatív hiba megmutatja, hogy mekkora a mért érték abszolút hibája. Általános szabály, hogy a relatív hibát százalékban fejezik ki:

Nézzünk meg egy példát. Mérjük meg a gömb átmérőjét egy mikrométerrel, amelynek műszeres hibája d \u003d 0,01 mm. Három mérés eredményeként a következő átmérőértékeket kaptuk:

d 1 \u003d 2,42 mm, d 2 \u003d 2,44 mm, d 3 \u003d 2,48 mm.

Az (A.1) képlet szerint meghatározzuk a gömbátmérő számtani középértékét

Ezután a Student együtthatóinak táblázata szerint kiderül, hogy 0,68 konfidenciaszint esetén három dimenzióban t n, p \u003d 1,3. Ezután az (A.2) képlet szerint kiszámítják a véletlenszerű mérési hibát Dd cl

Mivel a kapott véletlen hiba csak kétszerese az instrumentális hibának, akkor az abszolút mérési hiba megtalálásakor Dd az (A.3) szerint mind a véletlenszerű hibát, mind a műszerhibát figyelembe kell venni, azaz

Mm "± 0,03 mm.

A hibát száz milliméterre kerekítettük, mivel az eredmény pontossága nem haladhatja meg a mérőeszköz pontosságát, amely ebben az esetben 0,01 mm.

Tehát, a huzal átmérője

mm.

Ez a bejegyzés azt jelzi, hogy a gömbátmérő valós értéke 68% -os valószínűséggel a (2,42 × 2,48) mm intervallumban található.

A kapott érték relatív hibája (A.4) szerint:

%.