Középfokú általános műveltség

Vonal UMK G.K. Muravina. Algebra és a matematikai elemzés kezdetei (10-11) (mély)

Vonal UMK Merzlyak. Az algebra és az elemzés kezdetei (10-11) (U)

Matematika

Felkészülés a matematika vizsgára (profilszint): feladatok, megoldások és magyarázatok

Feladatokat elemezünk, példákat oldunk meg a tanárral

A profilszintű vizsgadolgozat időtartama 3 óra 55 perc (235 perc).

Minimális küszöb- 27 pont.

A vizsgadolgozat két részből áll, amelyek tartalmilag, összetettségükben és feladatok számában különböznek egymástól.

Az egyes munkarészek meghatározó jellemzője a feladatok formája:

• az 1. rész 8 feladatot tartalmaz (1-8. feladat), rövid válaszokkal egész szám vagy utolsó tizedes tört formájában;
• A 2. rész 4 feladatot (9-12. feladat) tartalmaz, egész szám vagy utolsó tizedes tört formájában, és 7 feladatot (13-19. feladat) részletes válasszal (a döntés teljes feljegyzése a döntés indoklásával). végrehajtott műveletek).

Panova Szvetlana Anatoljevna, az iskola legmagasabb kategóriájú matematika tanára, 20 év szakmai gyakorlat:

„Az iskolai bizonyítvány megszerzéséhez egy végzősnek két kötelező vizsgát kell tennie USE űrlapot, amelyek közül az egyik a matematika. A Matematikaoktatás Fejlesztési Koncepciójának megfelelően ben Orosz Föderáció A USE a matematikában két szintre oszlik: alapszintre és speciális szintre. Ma megvizsgáljuk a profilszintre vonatkozó lehetőségeket.

1. számú feladat- ellenőrzi az USE résztvevők képességét az elemi matematika 5-9. évfolyamán megszerzett ismereteik gyakorlati alkalmazására. A résztvevőnek rendelkeznie kell számítási készségekkel, tudnia kell racionális számokkal dolgozni, tudnia kell kerekíteni a tizedes törteket, képesnek kell lennie az egyik mértékegységet a másikra konvertálni.

1. példa Abban a lakásban, ahol Petr él, hidegvízmérőt (mérőt) szereltek fel. Május elsején 172 köbméter fogyasztást mutatott a mérő. m víz, június elsején pedig 177 köbméter. m. Milyen összeget kell fizetnie Péternek a hideg vízért májusra, ha az ára 1 cu. m hideg víz 34 rubel 17 kopecks? Válaszát rubelben adja meg.

Megoldás:

1) Keresse meg a havonta elköltött víz mennyiségét:

177-172 = 5 (cu m)

2) Keresse meg, mennyi pénzt kell fizetni az elhasznált vízért:

34,17 5 = 170,85 (dörzsölje)

Válasz: 170,85.

2. számú feladat- a vizsga egyik legegyszerűbb feladata. A végzettek többsége sikeresen megbirkózik vele, ami a funkciófogalom definíciójának birtoklását jelzi. A 2. számú feladattípus a követelménykodifikátor szerint a megszerzett ismeretek és készségek gyakorlati tevékenységben és mindennapi életben való felhasználására szolgáló feladat. A 2. feladat a mennyiségek közötti különféle valós összefüggések leírásából, függvények felhasználásából és grafikonjainak értelmezéséből áll. A 2. feladat a táblázatokban, diagramokban, grafikonokban bemutatott információk kinyerésének képességét teszteli. A diplomásoknak meg kell tudniuk határozni egy függvény értékét az argumentum értékével a függvény különböző megadási módjaival, és le kell írniuk a függvény viselkedését és tulajdonságait a grafikonja szerint. Arra is szükség van, hogy a függvénygráfból meg tudjuk találni a legnagyobb vagy legkisebb értéket, és a vizsgált függvények grafikonjait meg tudjuk építeni. Az elkövetett hibák véletlenszerűek a probléma körülményeinek olvasásakor, a diagram olvasásakor.

#ADVERTISING_INSERT#

2. példa Az ábra egy bányavállalat egy részvényének csereértékének változását mutatja 2017. április első felében. Április 7-én az üzletember 1000 darab részvényt vásárolt ebből a társaságból. Április 10-én a megvásárolt részvények háromnegyedét, április 13-án pedig az összes maradékot értékesítette. Mennyit veszített az üzletember ezeknek a műveleteknek a következtében?

Megoldás:

2) 1000 3/4 = 750 (részvények) - az összes megvásárolt részvény 3/4-ét teszi ki.

6) 247500 + 77500 = 325000 (rubel) - az üzletember 1000 részvény eladása után kapott.

7) 340 000 - 325 000 = 15 000 (rubel) - az üzletember minden művelet eredményeként elveszett.

Válasz: 15000.

3. számú feladat- az első rész alapszintű feladata, a „Planimetria” tantárgy tartalma szerint méri a geometriai alakzatokkal végzett cselekvések végrehajtásának képességét ellenőrzi. A 3. feladat teszteli a kockás papíron lévő figura területének kiszámításának képességét, a szögek fokmértékeinek kiszámítását, a kerületek kiszámítását stb.

3. példa Keresse meg egy kockás papírra rajzolt téglalap területét, amelynek cella mérete 1 cm x 1 cm (lásd az ábrát). Válaszát négyzetcentiméterben adja meg.

Megoldás: Az ábra területének kiszámításához használhatja a Peak képletet:

Ennek a téglalapnak a területének kiszámításához a Peak képletet használjuk:

S= B +	G
	2

ahol V = 10, G = 6, tehát

S = 18 +	6
	2

Válasz: 20.

Lásd még: Egységes fizikai államvizsga: rezgési feladatok megoldása

4. számú feladat- a „Valószínűségszámítás és statisztika” tantárgy feladata. Teszteljük azt a képességet, hogy a legegyszerűbb helyzetben ki tudjuk számítani egy esemény valószínűségét.

4. példa A körön 5 piros és 1 kék pont található. Határozza meg, mely sokszögek nagyobbak: azok, amelyeknek minden csúcsa piros, vagy amelyeknek az egyik kék csúcsa van. Válaszában jelölje meg, hogy az egyikből mennyivel több, mint a másikból!

Megoldás: 1) A kombinációk számának képletét használjuk n elemek által k:

amelynek minden csúcsa piros.

3) Egy ötszög minden piros csúcsával.

4) 10 + 5 + 1 = 16 sokszög minden piros csúcsgal.

amelynek csúcsai pirosak vagy egy kék csúcsgal.

amelynek csúcsai pirosak vagy egy kék csúcsgal.

8) Egy hatszög, amelynek csúcsai pirosak, és egy kék csúcs.

9) 20 + 15 + 6 + 1 = 42 sokszög, amelyek mindegyikének piros csúcsa vagy egy kék csúcsa van.

10) 42 - 16 = 26 sokszög, amely a kék pontot használja.

11) 26 - 16 = 10 sokszög - hány sokszög, amelynek az egyik csúcsa kék pont, több, mint sokszög, amelyben minden csúcs csak piros.

Válasz: 10.

5. számú feladat- az első rész alapszintje a legegyszerűbb egyenletek (irracionális, exponenciális, trigonometrikus, logaritmikus) megoldási képességét teszteli.

5. példa Oldja meg a 2 3 + egyenletet x= 0,4 5 3 + x .

Megoldás. Osszuk el ennek az egyenletnek mindkét oldalát 5 3 +-al x≠ 0, azt kapjuk

2 3 + x	= 0,4 vagy		2		3 + x	=	2	,
5 3 + x			5				5

ahonnan az következik, hogy 3 + x = 1, x = –2.

Válasz: –2.

6. számú feladat planimetriában geometriai mennyiségek (hosszok, szögek, területek) megtalálására, valós helyzetek modellezésére a geometria nyelvén. A megszerkesztett modellek tanulmányozása geometriai fogalmak és tételek segítségével. A nehézségek forrása általában a planimetria szükséges tételeinek tudatlansága vagy helytelen alkalmazása.

Egy háromszög területe ABC egyenlő 129. DE- oldallal párhuzamos középvonal AB. Keresse meg a trapéz területét EGY ÁGY.

Megoldás. Háromszög CDE háromszöghöz hasonló TAXI két sarokban, mivel a sarok a csúcsnál Cáltalános, szög CDE egyenlő a szöggel TAXI mint a megfelelő szögek DE || AB metsző AC. Mert DE a háromszög középvonala a feltétellel, majd a középvonal tulajdonságával | DE = (1/2)AB. Tehát a hasonlósági együttható 0,5. A hasonló ábrák területeit a hasonlósági együttható négyzeteként viszonyítjuk, tehát

Ennélfogva, S ABED = S Δ ABC – S Δ CDE = 129 – 32,25 = 96,75.

7. számú feladat- ellenőrzi a derivált alkalmazását a függvény tanulmányozására. A sikeres megvalósításhoz a származék fogalmának értelmes, nem formális birtoklása szükséges.

7. példa A függvény grafikonjára y = f(x) az abszcissza pontnál x 0 egy érintőt húzunk, amely merőleges a grafikon (4; 3) és (3; -1) pontjain átmenő egyenesre. megtalálja f′( x 0).

Megoldás. 1) Használjuk a két adott ponton átmenő egyenes egyenletét, és keressük meg a (4; 3) és (3; -1) pontokon átmenő egyenes egyenletét!

(y – y 1)(x 2 – x 1) = (x – x 1)(y 2 – y 1)

(y – 3)(3 – 4) = (x – 4)(–1 – 3)

(y – 3)(–1) = (x – 4)(–4)

–y + 3 = –4x+ 16| · (-1)

y – 3 = 4x – 16

y = 4x– 13, hol k 1 = 4.

2) Határozza meg az érintő meredekségét! k 2, amely merőleges az egyenesre y = 4x– 13, hol k 1 = 4, a következő képlet szerint:

3) Az érintő meredeksége a függvény deriváltja az érintkezési pontban. Eszközök, f′( x 0) = k 2 = –0,25.

Válasz: –0,25.

8. számú feladat- ellenőrzi a vizsgázók körében az elemi sztereometria ismereteit, képes-e képleteket alkalmazni az ábrák felületeinek és térfogatainak, kétszögletű szögeinek meghatározására, összehasonlítani a hasonló alakzatok térfogatát, tudjon műveleteket végrehajtani geometriai ábrákkal, koordinátákkal és vektorokkal stb. .

Egy gömb körül körülírt kocka térfogata 216. Határozzuk meg a gömb sugarát!

Megoldás. 1) V kocka = a 3 (hol A a kocka élének hossza), tehát

A 3 = 216

A = 3 √216

2) Mivel a gömb kockába van írva, ez azt jelenti, hogy a gömb átmérőjének hossza megegyezik a kocka élének hosszával, ezért d = a, d = 6, d = 2R, R = 6: 2 = 3.

9. számú feladat- megköveteli a végzetttől az algebrai kifejezések átalakítását és egyszerűsítését. 9. számú feladat haladó szint Nehézségek a rövid válaszokkal. Az USE „Számítások és átalakítások” szakaszában található feladatok több típusra oszlanak:

numerikus racionális kifejezések transzformációi;

algebrai kifejezések és törtek transzformációi;

numerikus/betűs irracionális kifejezések átalakítása;

fokozatokkal végzett cselekvések;

logaritmikus kifejezések átalakítása;

1. numerikus/betűs trigonometrikus kifejezések átalakítása.

9. példa Számítsa ki a tgα-t, ha ismert, hogy cos2α = 0,6 és

3π	< α < π.
4

Megoldás. 1) Használjuk a kettős argumentumképletet: cos2α = 2 cos 2 α - 1, és keressük meg

tan 2 α =	1	– 1 =	1	– 1 =	10	– 1 =	5	– 1 = 1	1	– 1 =	1	= 0,25.
	cos 2 α		0,8		8		4		4		4

Ezért tan 2 α = ± 0,5.

3) Feltétel szerint

3π	< α < π,
4

így α a második negyed és tgα szöge< 0, поэтому tgα = –0,5.

Válasz: –0,5.

#ADVERTISING_INSERT# 10. számú feladat- ellenőrzi a tanulók azon képességét, hogy a megszerzett korai ismereteket, készségeket a gyakorlati tevékenységben és a mindennapi életben hasznosítsák. Mondhatjuk, hogy ezek a fizikában és nem a matematikában problémák, de a feltételben minden szükséges képlet és mennyiség adott. A feladatok egy lineáris vagy másodfokú egyenlet, illetve egy lineáris vagy másodfokú egyenlőtlenség megoldására redukálódnak. Ezért meg kell tudni oldani az ilyen egyenleteket és egyenlőtlenségeket, és meg kell határozni a választ. A választ egész szám vagy utolsó tizedes tört formájában kell megadni.

Két tömegű test m= egyenként 2 kg, azonos sebességgel mozognak v= 10 m/s egymáshoz képest 2α szögben. Az abszolút rugalmatlan ütközésük során felszabaduló energiát (joule-ban) a kifejezés határozza meg K = mv 2 sin 2 α. Milyen legkisebb 2α szögben (fokban) kell elmozdulniuk a testeknek, hogy az ütközés következtében legalább 50 joule szabaduljon fel?
Megoldás. A feladat megoldásához meg kell oldanunk a Q ≥ 50 egyenlőtlenséget a 2α ∈ (0°; 180°) intervallumon.

mv 2 sin 2 α ≥ 50

2 10 2 sin 2 α ≥ 50

200 sin2α ≥ 50

Mivel α ∈ (0°; 90°), csak megoldjuk

Az egyenlőtlenség megoldását grafikusan ábrázoljuk:

Mivel α ∈ (0°; 90°) feltételezéssel azt jelenti, hogy 30° ≤ α< 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.

11. számú feladat- jellemző, de a diákok számára nehéznek bizonyul. A nehézségek fő forrása egy matematikai modell felépítése (egyenlet felállítása). A 11. számú feladat a szöveges feladatok megoldási képességét teszteli.

11. példa. A tavaszi szünetben a 11. osztályos Vasyának 560 edzésfeladatot kellett megoldania, hogy felkészüljön a vizsgára. Március 18-án, az utolsó tanítási napon Vasya 5 feladatot oldott meg. Aztán minden nap ugyanannyi problémát oldott meg többet, mint előző nap. Határozza meg, hány problémát oldott meg Vasya április 2-án, a vakáció utolsó napján.

Megoldás: Jelöli a 1 = 5 - azon feladatok száma, amelyeket Vasya március 18-án oldott meg, d- Vasya által megoldott feladatok napi száma, n= 16 - a napok száma március 18-tól április 2-ig, S 16 = 560 - a feladatok teljes száma, a 16 - azon feladatok száma, amelyeket Vasya április 2-án oldott meg. Tudva, hogy Vasya minden nap ugyanannyi feladatot oldott meg, mint előző nap, akkor a képleteket használhatja a számtani sorozat összegének meghatározásához:

560 = (5 + a 16) 8,

5 + a 16 = 560: 8,

5 + a 16 = 70,

a 16 = 70 – 5

a 16 = 65.

Válasz: 65.

12. számú feladat- ellenőrizze a tanulók függvényekkel végzett cselekvési képességét, tudja alkalmazni a deriváltot a függvény tanulmányozására.

Keresse meg egy függvény maximális pontját y= 10ln( x + 9) – 10x + 1.

Megoldás: 1) Keresse meg a függvény tartományát: x + 9 > 0, x> –9, azaz x ∈ (–9; ∞).

2) Keresse meg a függvény deriváltját:

4) A talált pont a (–9; ∞) intervallumhoz tartozik. Meghatározzuk a függvény deriváltjának előjeleit és ábrázoljuk a függvény viselkedését az ábrán:

A kívánt maximális pont x = –8.

Töltse le ingyen a matematika munkaprogramját az UMK G.K. sorára. Muravina, K.S. Muravina, O.V. Muravina 10-11 Töltse le az ingyenes algebrai kézikönyveket

13. számú feladat- megnövelt összetettségi szint részletes válasszal, amely az egyenletmegoldó képességet teszteli, a feladatok közül a legsikeresebben megoldott a fokozott összetettségű részletes válaszokkal.

a) Oldja meg a 2log 3 2 (2cos x) – 5log 3 (2 cos x) + 2 = 0

b) Keresse meg ennek az egyenletnek az összes gyökerét, szegmenshez tartozó.

Megoldás: a) Legyen log 3 (2cos x) = t, majd 2 t 2 – 5t + 2 = 0,

	log3(2cos x) =	2	⇔		2cos x = 9	⇔		kötözősaláta x =	4,5	⇔ mert |cos x| ≤ 1,
	log3(2cos x) =	1			2cos x = √3			kötözősaláta x =	√3
		2							2

akkor cos x =	√3
	2

	x =	π	+ 2π k
		6
	x = –	π	+ 2π k, k ∈ Z
		6

b) Keresse meg a szakaszon fekvő gyökereket.

Az ábrán látható, hogy az adott szakasznak vannak gyökerei

11π	És	13π	.
6		6

Válasz: A)	π	+ 2π k; –	π	+ 2π k, k ∈ Z; b)	11π	;	13π	.
	6		6		6		6

14. számú feladat- emelt szint a második rész feladataira utal részletes válasszal. A feladat a geometriai alakzatokkal végzett műveletek végrehajtásának képességét teszteli. A feladat két elemet tartalmaz. Az első bekezdésben bizonyítani kell a feladatot, a másodikban pedig kiszámítani.

A henger alapjának kerületi átmérője 20, a henger generatrixa 28. A sík 12 és 16 hosszúságú húrok mentén metszi az alapjait. A húrok távolsága 2√197.

a) Bizonyítsuk be, hogy a henger alapjainak középpontjai ennek a síknak ugyanazon az oldalán helyezkednek el.

b) Határozza meg e sík és a henger alapjának síkja közötti szöget!

Megoldás: a) Egy 12 hosszúságú húr = 8 távolságra van az alapkör középpontjától, és egy 16 hosszúságú húr, hasonlóan, 6 távolságra van. Ezért a vetületeik távolsága a körrel párhuzamos síkban van. A hengerek alapja vagy 8 + 6 = 14, vagy 8 - 6 = 2.

Ekkor az akkordok távolsága vagy

= = √980 = = 2√245

= = √788 = = 2√197.

A feltételnek megfelelően a második eset valósult meg, amelyben a húrok vetületei a henger tengelyének egyik oldalán fekszenek. Ez azt jelenti, hogy a tengely nem metszi ezt a síkot a hengeren belül, vagyis az alapok az egyik oldalán fekszenek. Amit bizonyítani kellett.

b) Jelöljük a bázisok középpontját O 1 és O 2 -vel. Húzzuk meg az alap középpontjából egy 12-es húrral a felező merőlegeset erre a húrra (hossza 8, mint már említettük), a másik alap közepétől pedig egy másik húrba. Ugyanabban a β síkban fekszenek, merőlegesek ezekre az akkordokra. Nevezzük a kisebb, A-nál nagyobb B húr felezőpontját és A vetületét a H második bázisra (H ∈ β). Ekkor AB,AH ∈ β és ezért AB,AH merőlegesek a húrra, vagyis az alap és az adott sík metszésvonalára.

Tehát a szükséges szög

∠ABH = arctán	AH	= arctg	28	= arctg14.
	BH		8 – 6

15. számú feladat- megnövekedett összetettségi szint részletes válasszal, ellenőrzi az egyenlőtlenségek megoldásának képességét, a feladatok közül a legsikeresebben megoldott, fokozott összetettségű részletes válasszal.

15. példa Oldja meg az egyenlőtlenséget | x 2 – 3x| napló 2 ( x + 1) ≤ 3x – x 2 .

Megoldás: Ennek az egyenlőtlenségnek a definíciós tartománya a (–1; +∞) intervallum. Tekintsünk három esetet külön-külön:

1) Hagyjuk x 2 – 3x= 0, azaz x= 0 vagy x= 3. Ebben az esetben ez az egyenlőtlenség igazzá válik, ezért ezek az értékek szerepelnek a megoldásban.

2) Hagyjuk most x 2 – 3x> 0, azaz x∈ (–1; 0) ∪ (3; +∞). Ebben az esetben ez az egyenlőtlenség átírható a ( x 2 – 3x) napló 2 ( x + 1) ≤ 3x – x 2 és ossza el egy pozitív kifejezéssel x 2 – 3x. 2. naplót kapunk ( x + 1) ≤ –1, x + 1 ≤ 2 –1 , x≤ 0,5 -1 vagy x≤ -0,5. Figyelembe véve a definíciós tartományt, megvan x ∈ (–1; –0,5].

3) Végül fontolja meg x 2 – 3x < 0, при этом x∈ (0; 3). Ebben az esetben az eredeti egyenlőtlenség átírásra kerül a (3 x – x 2) napló 2 ( x + 1) ≤ 3x – x 2. Pozitív kifejezéssel való osztás után 3 x – x 2 , 2. naplót kapunk ( x + 1) ≤ 1, x + 1 ≤ 2, x≤ 1. A területet figyelembe véve van x ∈ (0; 1].

A kapott megoldásokat összevonva kapjuk x ∈ (–1; –0.5] ∪ ∪ {3}.

Válasz: (–1; –0.5] ∪ ∪ {3}.

16. számú feladat- emelt szint a második rész feladataira utal részletes válasszal. A feladat a geometriai alakzatokkal, koordinátákkal és vektorokkal végzett műveletek végrehajtásának képességét teszteli. A feladat két elemet tartalmaz. Az első bekezdésben bizonyítani kell a feladatot, a másodikban pedig kiszámítani.

Egy 120°-os szögű ABC egyenlő szárú háromszögben az A csúcsban egy BD felezőszöget rajzolunk. A DEFH téglalapot az ABC háromszögbe úgy írjuk be, hogy az FH oldal a BC szakaszon, az E csúcs pedig az AB szakaszon legyen. a) Bizonyítsuk be, hogy FH = 2DH. b) Határozza meg a DEFH téglalap területét, ha AB = 4.

Megoldás: A)

1) ΔBEF - téglalap alakú, EF⊥BC, ∠B = (180° - 120°) : 2 = 30°, majd EF = BE a 30°-os szöggel ellentétes láb tulajdonsága miatt.

2) Legyen EF = DH = x, akkor BE = 2 x, BF = x√3 a Pitagorasz-tétel alapján.

3) Mivel ΔABC egyenlő szárú, akkor ∠B = ∠C = 30˚.

BD a ∠B felezőszöge, tehát ∠ABD = ∠DBC = 15˚.

4) Tekintsük ΔDBH - téglalap alakú, mert DH⊥BC.

2x	=	4 – 2x
2x(√3 + 1)		4

1	=	2 – x
√3 + 1		2

√3 – 1 = 2 – x

x = 3 – √3

EF = 3 - √3

2) S DEFH = ED EF = (3 - √3 ) 2(3 - √3 )

S DEFH = 24 - 12√3.

Válasz: 24 – 12√3.

17. számú feladat- részletes válaszú feladat, ez a feladat az ismeretek és készségek gyakorlati tevékenységben és a mindennapi életben való alkalmazását, a matematikai modellek építésének és feltárásának képességét teszteli. Ez a feladat gazdasági tartalmú szöveges feladat.

17. példa. A 20 millió rubel összegű letétet a tervek szerint négy évre nyitják meg. A bank minden év végén 10%-kal növeli a betétet az év eleji mérethez képest. Ezen túlmenően a harmadik és negyedik év elején a betétes évente pótolja a betétet x millió rubel, hol x - egész szám. megtalálja legmagasabb érték x, amelynél a bank négy év alatt kevesebb mint 17 millió rubelt fog hozzáadni a betéthez.

Megoldás: Az első év végén a hozzájárulás 20 + 20 · 0,1 = 22 millió rubel, a második év végén pedig 22 + 22 · 0,1 = 24,2 millió rubel lesz. A harmadik év elején a hozzájárulás (millió rubelben) (24,2+ x), és a végén - (24,2 + X) + (24,2 + X) 0,1 = (26,62 + 1,1 x). A negyedik év elején a hozzájárulás mértéke (26,62 + 2,1 X), és a végén - (26,62 + 2,1 x) + (26,62 + 2,1x) 0,1 = (29,282 + 2,31 x). Feltétel alapján meg kell találni a legnagyobb x egész számot, amelyre az egyenlőtlenség vonatkozik

(29,282 + 2,31x) – 20 – 2x < 17

29,282 + 2,31x – 20 – 2x < 17

0,31x < 17 + 20 – 29,282

0,31x < 7,718

x <	7718
	310

x <	3859
	155

x < 24	139
	155

Ennek az egyenlőtlenségnek a legnagyobb egész számú megoldása a 24.

Válasz: 24.

18. számú feladat- fokozott komplexitású feladat részletes válasszal. Ez a feladat a jelentkezők matematikai felkészültségének megnövekedett követelményeivel rendelkező egyetemek versenyeztetésére irányul. A nagy bonyolultságú feladat nem egy megoldási módszer alkalmazására, hanem különböző módszerek kombinációjára vonatkozik. A 18. feladat sikeres teljesítéséhez a szilárd matematikai ismeretek mellett magas szintű matematikai kultúra is szükséges.

Miben a egyenlőtlenségek rendszere

	x 2 + y 2 ≤ 2igen – a 2 + 1
	y + a ≤ |x| – a

pontosan két megoldása van?

Megoldás: Ez a rendszer átírható így

	x 2 + (y– a) 2 ≤ 1
	y ≤ |x| – a

Ha a síkon felrajzoljuk az első egyenlőtlenség megoldásainak halmazát, akkor a (0, A). A második egyenlőtlenség megoldásainak halmaza a síknak az a része, amely a függvény grafikonja alatt helyezkedik el y = | x| – a, az utóbbi pedig a függvény grafikonja
y = | x| , lefelé tolva A. Ennek a rendszernek a megoldása az egyes egyenlőtlenségek megoldáshalmazainak metszéspontja.

Következésképpen ennek a rendszernek csak az ábrán látható esetben lesz két megoldása. 1.

A kör és az egyenesek érintkezési pontjai a rendszer két megoldása lesz. Az egyenesek mindegyike 45°-os szöget zár be a tengelyekhez képest. Tehát a háromszög PQR- téglalap alakú egyenlőszárúak. Pont K koordinátái vannak (0, A), és a lényeg R– koordináták (0, – A). Ezen kívül vágások PRÉs PQ A kör sugara egyenlő 1-gyel.

QR= 2a = √2, a =	√2	.
	2

Válasz: a =	√2	.
	2

19. számú feladat- fokozott komplexitású feladat részletes válasszal. Ez a feladat a jelentkezők matematikai felkészültségének megnövekedett követelményeivel rendelkező egyetemek versenyeztetésére irányul. A nagy bonyolultságú feladat nem egy megoldási módszer alkalmazására, hanem különböző módszerek kombinációjára vonatkozik. A 19. feladat sikeres teljesítéséhez tudni kell megoldást keresni, az ismertek közül többféle megközelítést választani, módosítani a vizsgált módszereket.

Hadd snösszeg P egy aritmetikai sorozat tagjai ( a p). Ismeretes, hogy S n + 1 = 2n 2 – 21n – 23.

a) Adja meg a képletet! P ennek a fejlődésnek a tagja.

b) Keresse meg a legkisebb moduloösszeget! S n.

c) Keresse meg a legkisebbet! P, ahol S n egy egész szám négyzete lesz.

Megoldás a) Nyilvánvalóan a n = S n – S n- 1 . Ezt a képletet használva a következőket kapjuk:

S n = S (n – 1) + 1 = 2(n – 1) 2 – 21(n – 1) – 23 = 2n 2 – 25n,

S n – 1 = S (n – 2) + 1 = 2(n – 1) 2 – 21(n – 2) – 23 = 2n 2 – 25n+ 27

Eszközök, a n = 2n 2 – 25n – (2n 2 – 29n + 27) = 4n – 27.

B) mert S n = 2n 2 – 25n, majd fontolja meg a függvényt S(x) = | 2x 2 – 25x|. Az ő grafikonja az ábrán látható.

Nyilvánvaló, hogy a legkisebb értéket a függvény nulláihoz legközelebb eső egész pontokban érjük el. Nyilván ezek pontok. x= 1, x= 12 és x= 13. Mivel S(1) = |S 1 | = |2 – 25| = 23, S(12) = |S 12 | = |2 144 – 25 12| = 12, S(13) = |S 13 | = |2 169 – 25 13| = 13, akkor a legkisebb érték 12.

c) Az előző bekezdésből következik, hogy snóta pozitív n= 13. Mivel S n = 2n 2 – 25n = n(2n– 25), akkor az a nyilvánvaló eset, amikor ez a kifejezés tökéletes négyzet, akkor valósul meg, amikor n = 2n- 25, vagyis azzal P= 25.

Még ellenőrizni kell az értékeket 13 és 25 között:

S 13 = 13 1, S 14 = 14 3, S 15 = 15 5, S 16 = 16 7, S 17 = 17 9, S 18 = 18 11, S 19 = 19 13 S 20 = 20 13, S 21 = 21 17, S 22 = 22 19, S 23 = 23 21, S 24 = 24 23.

Kiderül, hogy kisebb értékeknél P teljes négyzet nem érhető el.

Válasz: A) a n = 4n- 27; b) 12; c) 25.

________________

*2017 májusa óta a DROFA-VENTANA közös kiadói csoport az Russian Textbook Corporation része. A társasághoz tartozott az Astrel kiadó és a LECTA digitális oktatási platform is. Alekszandr Brychkin, az Orosz Föderáció kormánya alá tartozó Pénzügyi Akadémián végzett, a közgazdasági tudományok kandidátusa, a DROFA kiadó innovatív projektjeinek vezetője a digitális oktatás területén (tankönyvek elektronikus formái, Orosz Elektronikus Iskola, LECTA digitális oktatás platform) főigazgatóvá nevezték ki. Mielőtt csatlakozott a DROFA kiadóhoz, az EKSMO-AST kiadó holding stratégiai fejlesztésért és befektetésekért felelős alelnöki posztját töltötte be. Ma az Orosz Tankönyvkiadó Corporation rendelkezik a szövetségi listán szereplő legnagyobb tankönyvportfólióval - 485 címmel (körülbelül 40%, nem számítva a szövetségi listán szereplő tankönyveket). gyógyiskola). A társaság kiadói birtokolják az orosz iskolák által leginkább keresett fizika, rajz, biológia, kémia, technológia, földrajz, csillagászat tankönyvkészleteit – az ország termelési potenciáljának fejlesztéséhez szükséges tudásterületeket. A társaság portfóliója tankönyveket és oktatási segédanyagokat tartalmaz Általános Iskola oktatási elnöki díjat kapott. Ezek olyan tankönyvek és kézikönyvek olyan témákról, amelyek szükségesek Oroszország tudományos, műszaki és ipari potenciáljának fejlesztéséhez.

Egy szabályos háromszög alakú piramis összes éle SBCD tetejére S egyenlők 9-el.

Bázis O Magasság ÍGY SS 1 , M- a borda közepe SB, pont L szélén fekszik CDÍgy CL : LD = 7: 2.

SBCD repülőgép S 1 LM- egyenlő szárú trapéz.

Megoldás.

a) Rajzolja meg a mediánt! S 1 M háromszög SS 1 B, amely metszi az egyenest BB 1 , amely egyben a háromszög mediánja is SS 1Bés indokok BCD, azon a ponton T. Akkor WT : tévé 1 = 4: 5.

Pont L, viszont felosztja a szegmenst B 1 D kapcsolatban DL : LV 1 = 4:5 azóta LD : LC= 2:7 és szegmens BB 1 - háromszög medián BCD.

Ezért a szakasz pontokon áthaladó oldala LÉs T, oldallal párhuzamosan BD okokból BCD. Hagyja a vonalat LT kereszteket időszámításunk előtt azon a ponton P.

Menj át a ponton M középvonal egy háromszögben SBD engedd át az oldalt SD azon a ponton K. Akkor PMKL- a szükséges szakaszt, és BP = DLÉs BM = KD. A háromszögek egyenlőségéből BMPÉs DKL kapunk MP = KL, ami azt jelenti PMKL- egyenlő szárú trapéz.

b) Nagyobb bázis PL trapéz 7, mert a háromszög LPC helyes. Második alap MK egyenlő 4,5-tel, mert MK- derékszögű háromszög középvonala SBD. Ezért a trapéz középvonala az

Vaszilij Ass 09.03.2016 14:53

miért a BT: TB1 = 4:5 megoldás 1. mondatában mi ez a tulajdonság? "mert BB1 az SS1B háromszög mediánja is." nincs ilyen tulajdonság

Schg Wrbutr 21.04.2017 19:58

Honnan veszed a 4:5 arányt? Meg tudod magyarázni a mediánok ezen tulajdonságát?

Alekszandr Ivanov

Egy háromszög mediánját 2:1 arányban osztjuk el a metszésponttal

Szabályos háromszög alakú piramisban SABC alapoldal AB 12, és az oldalsó él SA egyenlő 8. Pont MÉs N- a bordák közepe SAÉs SB illetőleg. Az α sík tartalmazza az egyenest MNés merőleges a gúla alapjának síkjára.

a) Bizonyítsuk be, hogy az α sík osztja a mediánt CE bázisok 5:1 arányban, a ponttól számítva C.

b) Határozza meg annak a gúlának a térfogatát, amelynek csúcsa a pont! C, és az alap a piramis egy szakasza SABCα sík.

Megoldás.

a) Egy szabályos háromszög alakú gúla alapjában egy egyenlő oldalú háromszög található. Magasság vetítés S piramisok az alapon ad egy pontot O, amely a mediánok metszéspontjában fekszik. Szóval a lényeg O a mediánokat 2:1 arányban osztja el, azaz.

Vegye figyelembe a magasságot SE háromszög SAB. Pont F 1 a közepe. Ezért vetülete a mediánra CE osztja a szegmenst OE félbe. Viszont a szegmens akkor

Ennek eredményeként értjük a lényeget F osztja a mediánt CE ponttól kezdve, vagy 5:1 arányban C. Q.E.D.

b) Határozza meg a kívánt gúla Medián magasságát! CE keresse meg a Pitagorasz-tétel alapján derékszögű háromszögből BCE:

Számítsa ki a piramis alapterületét (a trapéz területét! MNZK). Szegmens szegmens (mivel ez a háromszög középvonala ABS), a trapéz magassága Keresse meg a magasságot ÍGY derékszögű háromszögből SOC:

A trapéz (a piramis alapja) területe:

A piramis térfogatát a képlet határozza meg

Válasz: b)

Forrás: Anyagok USE szakértőknek 2016

a piramisban SABC az alap szabályos háromszög ABC oldalsó ponttal O- a piramis magasságának a tetejéről húzott alapja S.

a) Bizonyítsa be, hogy a lényeg O a háromszögön kívül esik ABC.

b) Határozza meg a négyszög gúla térfogatát! SABCO.

Megoldás.

a) Mert SA = SC, pont S a szakaszra merőleges síkban fekszik ACés áthaladva a közepén M. Ennélfogva, O egyenes vonalon fekszik BM. Jelöljük a piramis magasságát mint x, majd Következésképpen, és Sőt, ezért a lényeg O a háromszögön kívül esik. Sőt, mert AO BO, ráfekszik a folytatásra BM pontonként M.

b) Háromszögből SMA keresse meg Most, a háromszögből SMO keresse Akkor a háromszögből főnök nekünk van

Válasz:

Szabályos négyszög alakú piramisban SABCD tetejére S az alap oldala a 8. Pont L- a borda közepe SC. A vonalak közötti szög érintője BLÉs SA egyenlő

a) Legyen O- a piramis alapjának középpontja. Bizonyítsuk be, hogy a vonalak BOÉs LO merőlegesek.

b) Határozza meg a piramis felületét!

Megoldás.

a) Mivel a háromszög középvonala , De a három merőleges tétele szerint - a piramis alapjának síkjára való vetület egyenes Így, ill.

b) Legyen akkor , Ezenkívül , honnan Akkor a gúla oldallapjának magassága és a gúla felülete

Válasz: 192.

Forrás: Tipikus matematikai tesztfeladatok, szerkesztette: I. V. Yashchenko 2016

Egy szabályos négyszög gúla összes éle SABCD tetejére S egyenlőek 6. Magasság alap ÍGY ez a piramis a szakasz felezőpontja SS 1 , M- a borda közepe MINT, pont L szélén fekszik időszámításunk előttÍgy BL : LC = 1: 2.

a) Bizonyítsuk be, hogy a gúla szakasza SABCD repülőgép S 1 LM- egyenlő szárú trapéz.

b) Számítsa ki ennek a trapéznek a középvonalának hosszát!

Megoldás.

Egyenes S 1 Mátlépi a mediánt AO háromszög ABD azon a ponton TÍgy NÁL NÉL : NAK NEK= 2:1 mert T- a háromszög mediánjainak metszéspontja SAS 1 és O- az alap átlóinak metszéspontja ABCD, a piramis óta SABCD helyes.

Ennélfogva, NÁL NÉL : TC= 1:2. Pont L osztja a szegmenst időszámításunk előtt kapcsolatban BL : LC= 1:2, tehát háromszögek ACBÉs TCL hasonló a hasonlósági együtthatóval k = AC : TC = időszámításunk előtt : CL= 3:2, mivel közös szöget zárnak be a csúcsponttal Cés partik ACÉs időszámításunk előtt háromszögben ABC oldalakkal arányos TCÉs LC háromszög TCL ugyanazt a szöget zárja be. Tehát a szakasz pontokon átmenő oldala LÉs T, oldallal párhuzamosan AB a piramis alapjai SABCD HIRDETÉS azon a ponton P.

A szakasz ponton átmenő oldala M repülőn SAB, párhuzamos a vonallal AB, mivel a repülő S 1 LM keresztezi a repülőt SABés átmegy a vonalon PL, párhuzamos a síkkal SAB. A szakasznak ez az oldala metszi az oldalt SB azon a ponton K. Aztán a szakasz PMKL egyenlő szárú trapéz, hiszen AP = BLÉs AM = BK.

Nagyobb alap LP trapéz a 6, mert ABCD- négyzet. Második alap MK trapéz a 3, mert MK- a háromszög középvonala SAB. Tehát a trapéz mediánja az

Válasz: b) 4.5.

Háromszög alakú piramisban ABCD diéderszögek az éleken HIRDETÉSÉs időszámításunk előtt egyenlőek. AB = BD = DC = AC = 5.

a) Bizonyítsd be HIRDETÉS = időszámításunk előtt.

b) Határozza meg a gúla térfogatát, ha a diéder szöge a HIRDETÉSÉs időszámításunk előtt egyenlők 60°-kal.

Megoldás.

a) háromszög BAC- egyenlő szárú. Töltsük AM ⊥ időszámításunk előtt. M- középső időszámításunk előtt, Akkor DM ⊥ időszámításunk előtt, mivel a háromszög bdc egyenlő szárú. ∠ AMD időszámításunk előtt. Hasonlóan ∠ BNC= φ - a diéderszög lineáris szöge az élnél HIRDETÉS. Δ ABC = Δ DBC akkor három oldalról MA = MDÉs

Hasonlóképpen, Δ rossz = Δ CADÉs Megjegyzés = NC, A

háromszögek ANMÉs BMN közös lábon egyenlő MNés α hegyesszög, akkor AN = BM. De ennek következtében HIRDETÉS = időszámításunk előtt.

b) φ = 60° feltétellel, akkor a háromszög AMD egyenlő oldalú. Hadd HIRDETÉS = AM = MD = időszámításunk előtt = a, majd Háromszögben AMB van hol és

Válasz:

Forrás: Tasks 14 (C2) Egységes államvizsga 2016, Egységes államvizsga matematikából - 2016. Korai hullám, tartalék nap, A. Larin lehetőség (C rész).

Egy 12-es magasságú és 6-os alapsugarú derékszögű henger egyik alapjába húr van húzva. AB, megegyezik az alap sugarával, másik alapjába pedig egy átmérőt rajzolunk CD, merőleges AB. Szakasz épült ABNMáthalad a vonalon AB merőleges az egyenesre CD szóval az a pont Cés a henger alapjának középpontja, amelybe az átmérőt berajzolják CD, feküdjön a szakasz egyik oldalán.

a) Bizonyítsuk be, hogy ennek a szakasznak az átlói egyenlőek egymással.

b) Határozza meg a piramis térfogatát! CABNM.

Megoldás.

a) Metszet készítéséhez eldobjuk a merőlegeseket AMÉs BN a henger második alján. Szegmensek AMÉs BN párhuzamos és egyenlő, tehát ABNM- paralelogramma. Mivel egyenes AMÉs BN merőleges a henger alapjaira és különösen az egyenesre AB, paralelogramma ABNM egy téglalap. A téglalap átlói egyenlőek, amit igazolni kellett.

b) Egy téglalap területe ABNM egyenlő a Szegmenssel Ó egyenlő magassággal CH piramisok CABNM egyenlő Ezért a piramis térfogata CABNM egyenlő

Válasz: b)

Szabályos háromszög prizmában ABCA 1 B 1 C 1 minden él egyenlő 6. Az éleken AA 1 és CC 1 megjelölt pont MÉs N illetve, és AM = 2, CN = 1.

a) Bizonyítsuk be, hogy a sík MNB 1 a prizmát két poliéderre osztja, amelyek térfogata egyenlő.

b) Határozza meg a tetraéder térfogatát! MNBB 1 .

Megoldás.

A prizma alapterülete és a prizma térfogata

Négyszögletű piramisban B 1 A 1 C 1 NM A 1 B 1 C 1 oldallal lefelé A 1 C 1 , és egyenlő a Bázis értékkel A 1 C 1 NM piramisok B 1 A 1 C 1 NM egy trapéz, amelynek területe 27. Ebből következik a piramis térfogata B 1 A 1 C 1 NM egyenlő a prizma térfogatának felével. Ezért a poliéderek térfogatai B 1 A 1 C 1 NMÉs ABCMB 1 N egyenlőek.

b) Négyszögletű piramisban BACNM magassága megegyezik a prizma alapjának magasságával ABC, oldalra süllyesztve AC, és egyenlő a piramis alapjával BACNM egy trapéz, amelynek területe 9. A piramis térfogata BACNM egyenlő

Poliéder ABCMB 1 N két részből áll: BACNMÉs MNBB 1 . Tehát a tetraéder térfogata MNBB 1 egyenlő

Válasz:

Forrás: Tasks 14 (C2) USE 2016, USE - 2016. Early wave. Opció 201. Dél

Alekszandr Ivanov

Magassága egy egyenlő oldalú háromszögben, amelynek oldala 6

Van egy szabályos háromszög prizma ABCA 1 B 1 C 1 12 alapoldallal és 3 magassággal. Pont K- középső időszámításunk előtt, pont L oldalán fekszik A 1 B 1 szóval BAN BEN 1 L= 5. Pont M- középső A 1 C 1 .

pontokon keresztül KÉs L egy síkot úgy kell megrajzolni, hogy párhuzamos legyen egy egyenessel AC.

a) Bizonyítsuk be, hogy a fenti sík merőleges az egyenesre MB.

b) Határozzuk meg egy pontban csúcsos gúla térfogatát! BAN BENés amelynek alapja a prizma síkszelvénye.

Megoldás.

a) Jelölje be a pontokat és az éleken, illetve úgy, hogy Ekkor a sík legyen a sík

Nyilvánvaló, hogy mivel a síkra való vetület a háromszög magassága, merőleges, tehát a három merőleges tétel alapján

Tekintsük most egy pont vetületét egy síkra Mivel a vetület erre a síkra az él felezőpontja, akkor most bizonyítsuk be, hogy az egyenes merőleges Ekkor a három merőleges tétel szerint kiderül, hogy , és majd és

Jelölje a szakaszok metszéspontjával és a , és - a pontok vetületeivel és az egyenesre.

Tehát ezeknek a szögeknek az érintői egymással fordítottak, így a szögek összege 90°-ot ad, a szög pedig = 180° - 90° = 90°, amit bizonyítani kellett.

b) Nyilvánvaló, hogy mivel egyenlő oldalú háromszög.

Válasz:

Forrás: USE - 2016. Fő hullám 2016.06.06. Központ

Kocka átlós hossza ABCDA 1 B 1 C 1 D 1 egyenlő 3. A gerendán A 1 C megjelölt pont PÍgy A 1 P = 4.

a) Bizonyítsd be PBDC Az 1 egy szabályos tetraéder.

b) Határozza meg a szakasz hosszát! AP.

Megoldás.

a) Vezessünk be egy koordinátarendszert az ábrán látható módon! Mivel a kocka gyökér éle kisebb, mint az átlója, az adott kocka éle Ekkor a pontok B, D, C 1-nek van koordinátája.

Mert a P a folytatáson fekszik A 1 C, vonalszakasz A 1 Péles kocka átlójának tekinthető Akkor a pont P koordinátái vannak

Keresse meg a távolságot P pontokhoz D 1 , BÉs C 1:

Szegmensek C 1 B, D.B.És DC 1 - a kocka lapjainak átlói, ezért a Pitagorasz-tétel szerint akkor tehát a tetraéder összes éle DBC 1 P egyenlőek, tehát helyes.

b) Pontkoordináták A: Távolság a ponttól P lényegre törő A egyenlő

Válasz:

Vegyünk egy másik megoldást.

a) Egy kocka átlója nagyobb, mint az éle: Ezért

Vegye figyelembe, hogy az oldalsó négyzetek átlói AB. Aztán a háromszög időszámításunk előtt 1 D- helyes.

Hadd Mivel ABCD- van egy négyzetünk:

Mivel keresztben fekvő és függőleges is, így kapjuk: akkor két sarokban

Vegye figyelembe, hogy a háromszög derékszögű háromszög, akkor hol

Háromszögben OMC van: mivel - igaz. Ekkor az inverz Pitagorasz-tétel alapján Δ OMC− téglalap alakú, ∠ M= 90°.

A matematika alapszintű egységes államvizsga 13. feladatában egy függvény viselkedésének egyik fogalmának készségeit és ismeretét kell bemutatnia: deriváltak egy ponton vagy növekedési vagy csökkenési ütemek. Ennek a feladatnak az elméletét egy kicsit később adjuk hozzá, de ez nem akadályoz meg bennünket abban, hogy több tipikus lehetőséget részletesen elemezzünk.

A 14. sz. feladatok tipikus lehetőségeinek elemzése USE matematikai alapszinten

A feladat első verziója (demóverzió 2018)

A grafikon a hőmérséklet időtől való függését mutatja az autó motorjának felmelegedésének folyamatában. A vízszintes tengely a motor indítása óta eltelt időt mutatja percekben; a függőleges tengelyen a motor hőmérséklete Celsius fokban.

A grafikon segítségével minden időintervallumot igazítson a motor bemelegítési folyamatának jellemzőihez ebben az intervallumban.

A táblázatban minden betű alatt tüntesse fel a megfelelő számot.

Végrehajtási algoritmus:

1. Válassza ki azt az időtartamot, amely alatt a hőmérséklet csökkent.
2. Rögzítsen egy vonalzót 30°C-hoz, és határozza meg azt az időtartamot, amelyen belül a hőmérséklet 30°C alatt volt.

Megoldás:

Válasszuk ki azt az időintervallumot, amely alatt a hőmérséklet csökkent. Ez a szakasz szabad szemmel látható, a motor beindításától számítva 8 perccel kezdődik.

Vigyen fel egy vonalzót 30 °C-ra, és határozza meg azt az időtartamot, amelyen belül a hőmérséklet 30 °C alatt volt.

A vonalzó alatt a 0 - 1 perc időintervallumnak megfelelő szakasz lesz.

Ceruza és vonalzó segítségével megtudjuk, milyen időintervallumban volt a hőmérséklet 40 ° C és 80 ° C között.

A 40°C-nak és 80°C-nak megfelelő pontokból a merőlegeseket a grafikonra, a kapott pontokból pedig az időtengelyre ejtjük a merőlegeseket.

Látjuk, hogy ez a hőmérsékleti intervallum 3-6,5 perces időintervallumnak felel meg. Vagyis a feltételben megadottak közül 3 - 6 perc.

Válassza ki a hiányzó választ az eliminációs módszerrel.

A feladat második változata

FUNKCIÓGRAFOK

SZÁRMAZÉKOK GRAFIKAI

Megoldás:

Elemezzük az A függvény grafikonját. Ha a függvény növekszik, akkor a derivált pozitív és fordítva. A függvény deriváltja a szélsőpontokban nullával egyenlő.

Először az A függvény növekszik, azaz. a derivált pozitív. Ez megfelel a 2. és 3. derivált grafikonjainak. Az x = -2 függvény maximális pontján, vagyis ezen a ponton a deriváltnak nullával kell egyenlőnek lennie. Ez a feltétel a 3-as számú grafikonnak felel meg.

Először a B függvény csökken, azaz. a derivált negatív. Ez megfelel az 1. és 4. derivált grafikonjainak. Az x \u003d -2 függvény maximális pontja, vagyis ezen a ponton a derivált nullának kell lennie. Ez a feltétel a 4-es számú grafikonnak felel meg.

Először a B függvény növekszik, azaz. a derivált pozitív. Ez megfelel a 2. és 3. derivált grafikonjainak. Az x = 1 függvény maximális pontja, vagyis ezen a ponton a derivált nullával egyenlő. Ez a feltétel a 2-es számú grafikonnak felel meg.

Az eliminálás módszerével megállapíthatjuk, hogy a Г függvény grafikonja megfelel az 1-es számú derivált grafikonjának.

Válasz: 3421.

A feladat harmadik változata

Állítson fel egyezést a függvények grafikonjai és a származékaik grafikonjai között.

FUNKCIÓGRAFOK

SZÁRMAZÉKOK GRAFIKAI

Az egyes függvények végrehajtási algoritmusa:

1. Határozza meg a növekvő és csökkenő függvények intervallumát!
2. Határozza meg a függvények maximális és minimum pontjait!
3. Vonjon le következtetéseket, párosítsa össze a javasolt ütemterveket.

Megoldás:

Elemezzük az A függvény grafikonját.

Ha a függvény növekszik, akkor a derivált pozitív és fordítva. A függvény deriváltja a szélsőpontokban nullával egyenlő.

A szélsőpont az a pont, ahol a függvény maximális vagy minimális értékét elérjük.

Először az A függvény növekszik, azaz. a derivált pozitív. Ez megfelel a 3. és 4. derivált grafikonjainak. Az x=0 függvény maximális pontján, vagyis ezen a ponton a derivált nullával egyenlő. Ez a feltétel a 4-es számú grafikonnak felel meg.

Elemezzük a B függvény grafikonját.

Először a B függvény csökken, azaz. a derivált negatív. Ez megfelel az 1. és 2. derivált grafikonjainak. Az x=-1 függvény minimumpontja, vagyis ezen a ponton a deriváltnak nullának kell lennie. Ez a feltétel a 2-es számú grafikonnak felel meg.

Elemezzük a B függvény grafikonját.

Először a B függvény csökken, azaz. a derivált negatív. Ez megfelel az 1. és 2. derivált grafikonjainak. Az x \u003d 0 függvény minimális pontja, vagyis ezen a ponton a deriváltnak nullának kell lennie. Ez a feltétel az 1-es számú grafikonnak felel meg.

Az eliminálás módszerével megállapíthatjuk, hogy a Г függvény grafikonja megfelel a 3-as számú derivált grafikonjának.

Válasz: 4213.

A tizennegyedik feladat változata 2017

Az ábrán egy függvény grafikonja és az A, B, C és D abszcissza pontokban megrajzolt érintői láthatók.A jobb oldali oszlop a derivált értékeit mutatja az A, B, C és D pontokban. A grafikon segítségével párosítsa az egyes pontokat a függvény deriváltjának értékével.

PONTOK
A
BAN BEN
VAL VEL
D

SZÁRMAZÉKOS ÉRTÉKEK
1) –4
2) 3
3) 2/3
4) -1/2

Emlékezzünk vissza, mit jelent a derivált, nevezetesen az értékét a pontban - a derivált függvény értéke egy pontban egyenlő az érintő meredekségének (együtthatójának) érintőjével.

A válaszokban két pozitív és két negatív lehetőségünk van. Mint emlékszünk, ha az együttható közvetlen (grafika y = kx + b) pozitív, akkor az egyenes növekszik, ha negatív, akkor az egyenes csökken.

Két növekvő egyenesünk van - az A és D pontban. Most emlékezzünk, mit jelent a k együttható értéke?

A k együttható megmutatja, hogy a függvény milyen gyorsan növekszik vagy csökken (valójában maga a k együttható az y = kx + b függvény deriváltja).

Ezért k \u003d 2/3 egy gyengédebb egyenes vonalnak felel meg - D, és k \u003d 3 - A.

Hasonlóképpen negatív értékek esetén: a B pont egy meredekebb egyenesnek felel meg, ahol k = -4, a C pont pedig - -1/2.

A tizennegyedik feladat változata 2019-ben(1)

Az ábrán a pontok a fűtőtestek havi eladási volumenét mutatják egy háztartási gépboltban. A hónapok vízszintesen, az eladott fűtőtestek száma függőlegesen. Az érthetőség kedvéért a pontokat egy vonal köti össze.

Az ábra segítségével párosítsa a feltüntetett időszakokat a fűtőtestek értékesítési jellemzőivel.

Végrehajtási algoritmus

Elemezzük a grafikonnak megfelelő részeit különböző időpontokban az év ... ja. Megfogalmazzuk a grafikonon megjelenített helyzeteket. Megtaláljuk a számukra legmegfelelőbb válaszokat.

Megoldás:

Télen az eladások száma meghaladta a 120 db/hó értéket, és folyamatosan nőtt. Ez a helyzet megfelel a 3. válasznak. Azok. kapunk: A-3.

Tavasszal az eladások fokozatosan csökkentek a havi 120 fűtőberendezésről 50-re. Ehhez a megfogalmazáshoz a 2. lehetőség áll a legközelebb. Nekünk van: B–2.

A nyáron az eladások száma nem változott, minimális volt. Ennek a megfogalmazásnak a 2. része nem tükröződik a válaszokban, és csak a 4. sz. alkalmas az elsőre. Ezért rendelkezünk: AT 4.

Ősszel az eladások növekedtek, de számuk egyik hónapban sem haladta meg a 100 darabot. Ezt a helyzetet az 1. lehetőség írja le. Kapunk: G–1.

A 2019. évi tizennegyedik feladat változata (2)

A grafikon egy normál busz sebességének az időtől való függését mutatja. A függőleges tengely a busz sebességét mutatja km/h-ban, a vízszintes tengely a busz indulása óta eltelt időt percben.

A grafikon segítségével illessze az egyes időintervallumokat a busz mozgásának karakterisztikájához ebben az intervallumban.

Végrehajtási algoritmus

1. A felosztási árat vízszintes és függőleges skálán határozzuk meg.
2. Sorra elemezzük a jobb oldali oszlopból („Jellemzők”) javasolt 1–4. Összehasonlítjuk őket a táblázat bal oldali oszlopából származó időintervallumokkal, a válaszhoz "betű-szám" párokat találunk.

Megoldás:

A vízszintes skála osztásértéke 1 s, a függőleges skála 20 km/h.

1. Amikor a busz megáll, a sebessége 0. Egymás után 2 percig csak a 9. perctől a 11. percig volt nulla sebesség a busz. Ez az idő a 8-12 perces intervallumba esik. Tehát van pár válaszunk: B–1.
2. A busz sebessége több ideig 20 km/h vagy annál nagyobb volt. Sőt, az A lehetőség itt nem megfelelő, mert például a 7. percben 60 km/h volt a sebesség, a B opció - mert már alkalmazták, D lehetőség - mert az intervallum elején és végén a busz nulla sebessége volt. Ebben az esetben a B lehetőség megfelelő (12–16 perc); ebben az intervallumban a busz 40 km/h sebességgel indul, majd 100 km/m-re gyorsul, majd fokozatosan 20 km/h-ra csökkenti a sebességet. Tehát nekünk van: AT 2.
3. Itt van beállítva a sebességkorlátozás. Nem vesszük figyelembe a B és C lehetőséget. A többi A és G intervallum egyaránt megfelelő. Ezért helyes lenne először a 4. lehetőséget megfontolni, majd ismét visszatérni a 3. lehetőséghez.
4. A fennmaradó két intervallumból mindössze 4-8 perc alkalmas a 4. karakterisztikára, mivel ezen az intervallumon (a 6. percnél) volt megállás. A 18-22 perces intervallumban nem volt megállás. Kapunk: A-4. Ebből az következik, hogy a 3. számú karakterisztika esetében a Г intervallumot kell venni, azaz. kiderül egy pár G–3.

A 2019. évi tizennegyedik feladat változata (3)

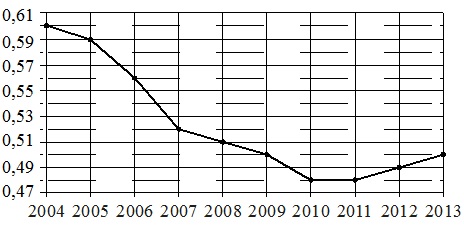
A pontozott ábra Kína népességének növekedését mutatja 2004 és 2013 között. Az évszámot horizontálisan, a százalékos népességnövekedést (az előző évhez viszonyított népességnövekedést) függőlegesen jelezzük. Az érthetőség kedvéért a pontokat egy vonal köti össze.

A diagram segítségével párosítsa az egyes jelzett időszakokat Kína népességnövekedésének jellemzőivel ebben az időszakban..

Végrehajtási algoritmus

1. Határozza meg a kép függőleges skálájának osztási értékét! Ez a különbség a szomszédos skálaértékek párja között osztva 2-vel (mivel két szomszédos érték között 2 osztás van).
2. A feltételben (bal oldali táblázatos oszlop) egymás után megadott 1-4 jellemzőket elemezzük. Mindegyiket összehasonlítjuk egy adott időszakkal (jobb oldali táblázat oszlop).

Megoldás:

A függőleges skála osztásértéke 0,01%.

1. A növekedés visszaesése 2004 és 2010 között folyamatosan folytatódott. 2010-2011-ben a növekedés folyamatosan minimális volt, 2012-től pedig növekedésnek indult. Azok. 2010-ben megállt a növekedés. Az idei év a 2009-2011 közötti időszakra esik. Ennek megfelelően rendelkezünk: AZ 1-BEN.
2. A növekedés legnagyobb visszaesését az ábra grafikonjának „legmeredekebben” eső vonalának kell tekinteni. A 2006-2007 közötti időszakra esik. és évi 0,04% (2006-ban 0,59–0,56=0,04%, 2007-ben 0,56–0,52=0,04%). Innen kapjuk: A-2.
3. A 3. számú jellemzőben jelzett növekedés 2007-ben kezdődött, 2008-ban folytatódott és 2009-ben ért véget. Ez a B időszaknak felel meg, azaz. nekünk van: B–3.
4. A népességnövekedés 2011 után kezdett növekedni, i.e. 2012-2013 között Ezért kapjuk: G–4.

A 2019. évi tizennegyedik feladat változata (4)

Az ábrán egy függvénygrafikon és az A, B, C és D abszcissza pontokban megrajzolt érintők láthatók.

A jobb oldali oszlop a függvény deriváltjának értékeit mutatja az A, B, C és D pontokban. A grafikon segítségével párosítsa az egyes pontokat a függvény deriváltjának értékével.

Végrehajtási algoritmus

1. Olyan érintőpárt tekintünk, amelynek hegyesszöge van az x tengely pozitív irányával. Összehasonlítjuk őket, megtaláljuk az egyezést a származékok megfelelő értékei között.
2. Az x tengely pozitív irányával tompaszöget bezáró érintőpárt tekintünk. Összehasonlítjuk őket modulo módon, meghatározzuk a derivált értéküknek való megfelelést a jobb oldali oszlopban maradó kettő között.

Megoldás:

Az x tengely pozitív irányú hegyesszögét a t.B és t.C deriváltjai képezik. Ezeknek a származékoknak pozitív értékei vannak. Ezért itt az 1-es és a 3-as értékek közül kell választani. Alkalmazva azt a szabályt, hogy ha a szög kisebb, mint 45 0, akkor a derivált kisebb, mint 1, és ha több, akkor nagyobb, mint 1, arra a következtetésre jutunk, hogy a t.B-ben a modulo derivált nagyobb, mint 1, a t.C-ben - kisebb, mint 1. Ez azt jelenti, hogy a válaszhoz párokat hozhat létre: AT 3És S-1.

A t.A és t.D deriváltjai tompaszöget zárnak be az x tengely pozitív irányával. És itt is ugyanezt a szabályt alkalmazzuk, kissé átfogalmazva: minél jobban „nyomódik” a pont érintője az abszcissza tengelyének egyeneséhez (annak negatív irányába), annál nagyobb abszolút értékben. Ekkor azt kapjuk, hogy az A pontban lévő derivált abszolút értékben kisebb, mint a D pontban lévő derivált. Innentől van párunk a válaszhoz: A-2És D-4.

A 2019. évi tizennegyedik feladat változata (5)

Az ábrán a pontok a 2011. januári moszkvai átlagos napi levegőhőmérsékletet mutatják. A hónap dátumai vízszintesen, a Celsius-fokban mért hőmérsékletek függőlegesen vannak feltüntetve. Az érthetőség kedvéért a pontokat egy vonal köti össze.

Az ábra segítségével párosítsa a feltüntetett időszakokat a hőmérséklet-változás jellemzőivel.

Végrehajtási algoritmus

Sorrendben elemezzük az 1–4. jellemzőket (jobb oszlop), az ábra grafikonja segítségével. Mindegyiket egy adott időszakhoz igazítjuk (bal oldali oszlop).

Megoldás:

1. Hőmérséklet-emelkedés csak az időszak végén, január 22-28-án volt megfigyelhető. Itt 27-én és 28-án 1, illetve 2 fokkal emelkedett. Az időszak végén január 1–7-én stabil volt a hőmérséklet (–10 fok), január 8–14-én és 15–21-én csökkent (-1-ről –2-re, illetve –11-ről –12-re). fok, ill. Ezért kapjuk: G–1.
2. Mivel minden időszak 7 napot ölel fel, a hőmérsékletet minden periódus 4. napjától kezdődően kell elemezni. A hőmérséklet csak január 4-7 között maradt 3-4 napig változatlan. Tehát megkapjuk a választ: A-2.
3. A havi minimum hőmérsékletet január 17-én figyelték meg. Ez a szám a január 15–21-i időszakra esik. Innentől van egy párunk: AT 3.
4. A hőmérséklet maximum január 10-én esett le, és +1 fok volt. Ez az időpont január 8-14-re esik. Tehát nekünk van: B-4.

A 2019. évi tizennegyedik feladat változata (6)

Az ábra az y \u003d f (x) függvény grafikonját mutatja, valamint az Ox tengelyen jelölt A, B, C és D pontokat.

A grafikon segítségével párosítsa az egyes pontokat a függvény jellemzőivel és deriváltjával

Végrehajtási algoritmus

1. A függvény értéke egy pontban pozitív, ha ez a pont az Ox tengely felett helyezkedik el.
2. A derivált egy pontban nagyobb nullánál, ha az adott pont érintője hegyesszöget zár be az x tengely pozitív irányával.

Megoldás:

Az A pont az Ox tengely alatt van, ami azt jelenti, hogy a benne lévő függvény értéke negatív. Ha egy érintőt húzunk bele, akkor a szög és az Ox pozitív irány között kb. 90 0 lesz, azaz. hegyesszöget alkot. Tehát ebben az esetben a 3-as karakterisztikus szám megfelelő. Azok. nekünk van: A-3.

B pont Az ökör tengelye felett helyezkedik el, azaz. a pontnak pozitív függvényértéke van. Az érintő ezen a ponton meglehetősen közel lesz az abszcissza tengelyéhez, és pozitív irányával tompaszöget (valamivel kisebb, mint 180 0) képez. Ennek megfelelően a derivált ezen a ponton negatív. Így itt az 1. karakterisztika megfelelő. A választ kapjuk: AZ 1-BEN.

C pont A pont az Ox tengely alatt helyezkedik el, a benne lévő érintő nagy tompaszöget zár be az abszcissza tengely pozitív irányával. Azok. t.C-ben mind a függvény, mind a derivált értéke negatív, ami a 2. számú jellemzőnek felel meg. Válasz: S-2.

D pont. A pont az Ox tengely felett helyezkedik el, és a benne lévő érintő hegyesszöget zár be a tengely pozitív irányával. Ez arra utal, hogy itt a függvény és a derivált értéke is nagyobb, mint nulla. Válasz: D-4.

A 2019. évi tizennegyedik feladat változata (7)

Az ábrán a pontok a hűtőszekrények havi eladási volumenét mutatják egy háztartási gépboltban. A hónapok vízszintesen, az eladott hűtőszekrények száma függőlegesen. Az érthetőség kedvéért a pontokat egy vonal köti össze.

Az ábra segítségével párosítsa a feltüntetett időszakokat a hűtőszekrények értékesítésének jellemzőivel.

Végrehajtási algoritmus

1. Ha meg kell találnia a hűtőszekrények számát egy adott időszakra, akkor három hónapra meg kell határoznia azok mennyiségét.
2. Az 1–4. jellemzőket elemezni kell (jobb oszlop), mindegyiknek megfelelő időszakot találva (bal oldali oszlop).

Megoldás:

Elemezzük a jellemzőket:

1. A legkevesebb hűtőszekrényt az év elején és végén adják el. Ezért vegyük figyelembe a január-március és az október-december időszakot. Január-márciusban hozzávetőleg 250+250+300=800, október-decemberben pedig hozzávetőleg 350+200+100=650 hűtőszekrényt értékesítettek. Ez azt jelenti, hogy az utolsó időszak még alkalmas ide. Válasz: G–1.
2. Áprilistól júliusig az eladások hosszú távú növekedése volt megfigyelhető. Ez az idő a teljes április-június időszakot fedi le, és a következő időszak kezdetét rögzíti. Ezért kapjuk: B–2.
3. Itt is meg kell találni a teljes időszakokra eladott egységek összegét. Az 1. és az utolsó időszakra már megtalálták (lásd 1. pont). 2. és 3.-ra számolunk, így kapjuk: 300+400+600=1300 - április-júniusban, megközelítőleg 650+600+550=1800 - július-szeptember. Az értékesítési volumen január-márciusban a lehető legközelebb van a szükséges 800 hűtőszekrényhez. Ezért rendelkezünk: A-3.
4. Az eladások azonos csökkenése azt jelenti, hogy az eladott hűtőszekrények száma közötti különbségnek ugyanannyinak kell lennie. Július végétől az eladások visszaesése volt megfigyelhető. Augusztusban 650-600=50 db, szeptemberben 600-550=50 db volt a csökkenés. Továbbá októberben már 550–350=200 hűtőszekrény, novemberben 350–200=150, decemberben 200–100=100 volt a különbség. Így belefér ez az eset Július-szeptember időszak. Válasz: AT 4.

A 2019. évi tizennegyedik feladat változata (8)

A pontozott ábra az oroszországi külszíni bányászat éves mennyiségét mutatja 2001 és 2010 között. Az évszám vízszintesen, a széntermelés millió tonnában kifejezett mennyisége függőlegesen van feltüntetve. Az érthetőség kedvéért a pontokat vonalak kötik össze.

Az ábra segítségével párosítsa a jelzett időszakokat az adott időszak széntermelésének jellemzőivel..

Végrehajtási algoritmus

1. Azokat a pontokat, amelyek nem esnek a függőleges tengely skálájának pontos értékére, hozzávetőlegesen határozzuk meg.
2. Sorra elemezzük a megadott (jobb oszlopban) jellemzőket ezzel a grafikonnal. Meghatározzuk mindegyikük megfelelését egy adott időszaknak.

Elemezzük a jellemzőket:

1. A termelés mennyisége 190 millió tonnánál kevesebb volt a 2001 és 2005 közötti időszakban. Aztán a termelés visszaesését 2009-ben rögzítették, de egy év nem időszak. A 2001–2005-ös évek teljes egészében az A (2002–2004) időszakba esnek. Tehát megkapjuk a választ: A–1.
2. Ez a „volumen… először csökkent, majd növekedni kezdett” megfogalmazás 2 időszaknak felel meg – 2002–2003. és 2009–2010 De azóta ezen időszakok közül az elsőt már válasznak vettük, akkor helyénvaló itt egy pár használata G–2.
3. A 3. jellemzőben leírt helyzet a legpontosabban a 2006–2008 közötti időszakban tükröződik. Ebben az időben a termelés először fokozatosan emelkedett (körülbelül 190 millió tonnáról 210-re), majd meredeken emelkedett 250 millió tonnára. megfelelő válasz itt: 2006–2008 és ennek megfelelően rendelkezünk: AT 3.
4. A lassú növekedést abban az időszakban kell keresni, amikor a grafikon vonalának a legszelídebb formája van. Ezek a következők: 2004–2006, ami a B időszaknak felel meg, i.e. kapunk: B–4.

A 2019. évi tizennegyedik feladat változata (9)

A grafikon a hőmérséklet időtől való függését mutatja az autó motorjának felmelegedésének folyamatában. A vízszintes tengely a motor indítása óta eltelt időt mutatja percben, a függőleges tengely pedig a motor hőmérsékletét Celsius-fokban.

A grafikon segítségével minden időintervallumot párosítson egy hőmérsékleti jellemzővel.

Végrehajtási algoritmus

Először elemezzük a következő jellemzőt, majd összehasonlítjuk egy adott időintervallumtal.

Megoldás:

1. 60 0 felett volt a hőmérséklet a 4. perctől a 7. percig. Ezért itt 4-6 perces intervallumot kell venni. Kapunk: AZ 1-BEN.
2. A hőmérséklet csak a 7. perc után csökkent. Ennek megfelelően itt 7-9 perces intervallum megfelelő. Válasz: G–2.
3. A leggyorsabb hőmérséklet-emelkedés ott következett be, ahol a grafikonon a legmeredekebb a függőleges emelkedés. Ez csak a felfűtés 1. percében megy végbe. Azok. megfelelő intervallum 0-1 perc. Válasz: A-3.
4. A hőmérséklet 40-50 0 С között zajlott, a 2. perctől a 3. percig. Tehát 2-3 perces intervallumot kell választania. Válasz: B–4.

A 2019. évi tizennegyedik feladat változata (10)

A grafikon a tornász pulzusszámának az időtől való függését mutatja a talajgyakorlatokban végzett teljesítménye alatt és után. A vízszintes tengelyen a tornász teljesítményének kezdete óta eltelt idő (percben), a függőleges tengelyen a pulzusszám (percenkénti ütésben) látható.

A grafikon segítségével párosítsa az egyes időintervallumokat a tornász pulzusának karakterisztikájával ebben az intervallumban.

Végrehajtási algoritmus

1. A jellemző elemzéséhez csak a grafikon 1. felét kell használni.
2. Azon gráfpontok esetében, amelyek nem esnek az ábra rácsának „csomópontjaiba” (tehát amelyeknél nem lehet pontos értékeket meghatározni), hozzávetőlegesen meg kell határozni az értékeket.
3. Az impulzus növekedésének nagysága összefügg a grafikonvonal síkságával (vagy fordítva, meredekségével). Ez azt jelenti, hogy minél nagyobb változás következik be a függvény értékében egy-egy (de szükségszerűen azonos) időtartam alatt, annál nagyobb a növekedés.

Megoldás:

Elemezzük a javasolt jellemzőket:

1. Ha a pulzusszám először csökkent, majd nőtt, akkor a grafikonon ezt a grafikon vonalának "elhajlásában" kell kifejezni. Az ilyen görbület csak 3-4 percig figyelhető meg. Tehát megkapjuk a választ: G–1.
2. A diagram 1. felében látható vonal legnagyobb "emelkedése" az 1. perctől a 2. percig megy végbe. Innen kapjuk: B–2.
3. A pulzusszám a 2. perctől kezdve csökkent. 3-4 percen belül zuhanás is megfigyelhető volt, de aztán növekedésbe fordult. Ezért a helyes intervallumot itt B-nek kell tekinteni. Így a válasz: AT 3.
4. Az egyetlen intervallum, amelyben a frekvencia nem haladta meg a 100 ütést, 0-1 perc volt. Innentől megkaptuk a választ: A-4.

Állítson fel egyezést a függvények grafikonjai és a függvények jellemzői között a [-1 szegmensen; 1].

[b] JELLEMZŐK

1) a függvény növekszik a [-1; 1]
2) a függvény csökken a szegmensen [-1; 1]
3) a függvénynek van egy minimumpontja a [-1] intervallumon; 1]
4) a függvénynek a [-1] intervallumon van egy maximumpontja; 1]

A diagram a USE rövidítésre a Google keresőoldalán végzett keresések számát mutatja 2015 szeptemberétől 2016 augusztusáig. A hónapok és évek vízszintesen, az adott hónapra vonatkozó kérések száma pedig függőlegesen van feltüntetve.

A diagram segítségével állapítson meg kapcsolatot az időintervallumok és a kérések számában bekövetkezett változás jellege között.

[b] IDŐK
A) ősz
B) Tél
B) tavasz
D) Nyár

[b] A SZÁMVÁLTOZÁSI KÉRELEM JELLEGE
1) A kérelmek számának meredek csökkenése
2) A kérelmek száma gyakorlatilag nem változott
3) A kérelmek száma fokozatosan csökkent
4) A kérelmek száma zökkenőmentesen nőtt

Írja le a számokat válaszul, a betűknek megfelelő sorrendbe rendezve őket:

A grafikon a tornász pulzusszámának az időtől való függését mutatja a talajgyakorlatokban végzett teljesítménye alatt és után.
A vízszintes tengelyen a tornász teljesítményének kezdete óta eltelt idő (percben), a függőleges tengelyen a pulzusszám (percenkénti ütemben).

A grafikon segítségével párosítsa az egyes időszakokat a tornász pulzusának jellemzőivel ebben az időszakban.

A táblázat a cég bevételeit és kiadásait mutatja 5 hónapra.

A táblázat segítségével párosítsa a feltüntetett időszakokat a bevételek és kiadások jellemzőivel.

A táblázatban minden betű alatt tüntesse fel a megfelelő számot.

Az ábrán a pontok a 2011. januári moszkvai átlagos napi levegőhőmérsékletet mutatják. A hónap dátumai vízszintesen, a Celsius-fokban mért hőmérsékletek függőlegesen vannak feltüntetve. Az érthetőség kedvéért a pontokat egy vonal köti össze.
Az ábra segítségével párosítsa a feltüntetett időszakokat a hőmérséklet-változás jellemzőivel.

A grafikon egy autó sebességének az időtől való függését mutatja. A függőleges tengely az autó sebességét mutatja km/h-ban, a vízszintes tengely az autó mozgásának megkezdése óta eltelt időt másodpercben.

A grafikon segítségével párosítsa az egyes időszakokat az autó mozgásának jellemzőivel ebben az intervallumban.

IDŐSZAKOK

A) 0-30s
B) 60-60 s
C) 60-90 s
D) 90-120 s

JELLEMZŐK

1) az autó sebessége elérte a maximumot az autó teljes mozgása alatt
2) a jármű sebessége nem csökkent és nem haladta meg a 40 km/h-t
3) az autó 15 másodpercre megállt
4) az autó sebessége nem nőtt a teljes intervallum alatt

A
B
C
D

SZÁRMAZÉKOS ÉRTÉKEK

1) -4
2) 3
3) 2/3
4) -1/2

A táblázatban minden betű alatt tüntesse fel a megfelelő számot.

A grafikon a hőmérséklet időtől való függését mutatja az autó motorjának felmelegedésének folyamatában. A vízszintes tengely a motor indítása óta eltelt időt mutatja percekben; a függőleges tengelyen - a motor hőmérséklete Celsius fokban.

A grafikon segítségével minden időintervallumot igazítson a motor bemelegítési folyamatának jellemzőihez ebben az intervallumban.

IDŐintervallumok

A) 0-1 perc.
B) 1-3 perc.
B) 3-6 perc.
D) 8-10 perc.

JELLEMZŐK

1) a leglassabb hőmérséklet-emelkedés
2) a hőmérséklet leesett
3) a hőmérséklet 40 °C és 80 °C között volt
4) a hőmérséklet nem haladja meg a 30 °C-ot.

Az ábrán egy függvénygrafikon és az A, B, C és D abszcissza pontokban megrajzolt érintők láthatók.
A jobb oldali oszlop a függvény deriváltjának értékeit mutatja az A, B, C és D pontokban. A grafikon segítségével párosítsa az egyes pontokat a függvény deriváltjának értékével.

A grafikon a batiszkáf süllyedési sebességének időfüggőségét mutatja. A függőleges tengelyen a sebesség m/s-ban, a vízszintesen - a merülés kezdete óta eltelt idő másodpercben.

A grafikon segítségével illessze az egyes időintervallumokat a batiszkáf ezen időközönkénti alámerülési jellemzőihez.

IDŐintervallumok

A) 60-150 c
B) 150-180 c
B) 180-240 °C
D) 240-300 s

JELLEMZŐK

1) A batiszkaf 45 másodpercig állandó sebességgel süllyedt.
2) Csökkent az ereszkedés üteme, majd fél perces megállás következett.
3) A süllyedési sebesség elérte minden idők csúcsát.
4) A süllyedési sebesség nem nőtt a teljes intervallumban, de a batiszkáf nem állt meg.

A táblázatban minden betű alatt tüntesse fel a megfelelő számot.

Az ábra az y \u003d f (x) függvény grafikonját mutatja, és az Ox tengelyen jelölt A, B. C és D pontokat. A grafikon segítségével párosítsa az egyes pontokat a függvény jellemzőivel és deriváltjával.

A) A
IDŐSZÁMÍTÁSUNK ELŐTT
IDŐSZÁMÍTÁSUNK ELŐTT
D) D

A FUNKCIÓ ÉS A SZÁRMAZÉK JELLEMZŐI

1) a függvény értéke a pontban negatív, és a függvény deriváltjának értéke a pontban negatív

2) a függvény értéke a pontban pozitív, és a függvény deriváltjának értéke a pontban pozitív

3) a függvény értéke a pontban negatív, és a függvény deriváltjának értéke a pontban pozitív

4) a függvény értéke a pontban pozitív, és a függvény deriváltjának értéke a pontban nulla

Az ábrán az y=f(x) függvény grafikonja látható. A, b, c, d és e pontok
állítson be intervallumokat az x tengelyen. A grafikon segítségével párosítson minden intervallumot egy függvény karakterisztikájával vagy deriváltjával.

Az ábrán az y=f(x) függvény grafikonja látható. A, b, c, d és e pontok
állítson be intervallumokat az x tengelyen. A grafikon segítségével párosítson minden intervallumot egy függvény karakterisztikájával vagy deriváltjával.

A diagram azt mutatja, hogy egy háztartási gépboltban mekkora havi értékesítési volumenű hűtőszekrények történtek az év során. A hónapok vízszintesen, az eladott hűtőszekrények száma függőlegesen.

A diagram segítségével párosítsa a feltüntetett időszakokat a termék értékesítési jellemzőivel.

A) január-március
B) Április-június
B) július-szeptember
D) október-december

ELADÁSI LEÍRÁS

1) az eladások legnagyobb növekedése
2) az eladások legkisebb növekedése
3) elérte történelmi mélypontját
4) minden idők csúcspontja

Az ábrán látható pontok É-i város légköri nyomását mutatják 2013. április 4-től április 6-ig három napon át. Napközben 4 alkalommal mérik a nyomást: 0:00-kor, 6:00-kor, 12:00-kor és 18:00-kor. A napszak és a dátum vízszintesen, a nyomás higanymilliméterben pedig függőlegesen van feltüntetve. Az érthetőség kedvéért a pontokat vonalak kötik össze.

Az ábrán a pontok a fűtőtestek havi eladási volumenét mutatják egy háztartási gépboltban. A hónapok vízszintesen, az eladott fűtőtestek száma függőlegesen. Az érthetőség kedvéért a pontokat egy vonal köti össze.

Az ábra a társaság részvényeinek árfolyamát mutatja a 2013. szeptember 1. és szeptember 14. közötti időszakban. A hónap dátumai vízszintesen, a rubelben kifejezett részvényárfolyamok függőlegesen vannak feltüntetve.

A diagram segítségével párosítsa a feltüntetett időszakokat a részvényárfolyam jellemzőivel.
A) szeptember 1-3 1) a leggyorsabb áresés
B) Szeptember 4-6 2) az egész időszak alatt nőtt
C) szeptember 7-9. 3) a leglassabb áresés
D) Szeptember 9-11 4) az ár először emelkedett, majd csökkenni kezdett

A grafikon egy normál busz sebességének az időtől való függését mutatja. A függőleges tengelyen a busz sebessége km / h-ban, a vízszintesen - a busz indulása óta eltelt idő percekben

INTERVALLUMOK JELLEMZŐI
MOZGÁSI IDŐ
A) 4-8 perc 1) 2 perces megállás volt
B) 8-12 perc 2) a sebesség legalább 20 km/h a teljes intervallumban
C) 12-16 perc 3) a sebesség nem haladja meg a 60 km/h-t
D) 18-22 perc 4) 1 perces megállás volt

A diagram a társaság részvényeinek árfolyamát mutatja a 2013. szeptember 1. és szeptember 14. közötti időszakban. A hónap dátumai vízszintesen, a rubelben kifejezett részvényárfolyamok függőlegesen vannak feltüntetve. A diagram segítségével párosítsa a feltüntetett időintervallumokat a részvényárfolyam jellemzőivel.

Az ábrán látható pontok É-i város légköri nyomását mutatják 2013. április 4-től április 6-ig három napon át. Napközben 4 alkalommal mérik a nyomást: 0:00-kor, 6:00-kor, 12:00-kor és 18:00-kor. A napszak és a dátum vízszintesen, a nyomás higanymilliméterben pedig függőlegesen van feltüntetve. Az érthetőség kedvéért a pontokat vonalak kötik össze. Az ábra segítségével párosítsa a jelzett időszakokat az É város légköri nyomásának jellemzőivel ebben az időszakban.

itthon

Hogyan készüljünk fel a 14. sz. egységes államvizsga sztereometriai feladatok megoldására | 1C: Oktató

Ahogy a matematika profilvizsga eredménye is mutatja, a geometria feladatok a legnehezebbek a végzősök számára. Ennek ellenére legalább részben megoldható, ami azt jelenti, hogy az összesített eredményhez további pontokat lehet szerezni. Ehhez persze sokat kell tudni a geometriai formák "viselkedéséről", és ezt a tudást alkalmazni kell a problémák megoldására. Itt megpróbálunk néhány ajánlást adni a sztereometria problémájának megoldására való felkészüléshez.

Amit a KIM USE opció 14. számú sztereometria feladatáról tudni kell

Ez a feladat általában két részből áll:

bizonyíték, amelyben a geometriai testek adott konfigurációjára vonatkozó állítás bizonyítására kell kérni;

számítástechnika, amelyben meg kell találnia egy bizonyos értéket a feladat első részében bizonyított állítás alapján.

Ennek a feladatnak a megoldásáért a 2018-as matematika vizsgán a maximumot kaphatja két elsődleges pontszám. A feladatnak csak a „bizonyítékot” vagy csak a „számítási” részét szabad megoldani, és ebben az esetben egy elsődleges pontot szerezni.

Sok iskolás a vizsgán ne is kezdd a 14. feladat megoldásához, bár az sokkal egyszerűbb, pl. a 16. feladat - planimetria szempontjából.

A 14. feladat hagyományosan csak néhány kérdést tartalmaz a sztereometrikus problémákra vonatkozó lehetséges kérdések közül:

távolságok megtalálása a térben;

szögek keresése a térben;

poliéderszakasz felépítése síkkal;

ennek a szakasznak a területe vagy annak a poliédernek a térfogata, amelyre ez a sík felosztotta az eredeti poliédert.
Ezekkel a kérdésekkel összhangban a felkészülés a feladatra.

Először természetesen tanulni kell minden szükséges axiómát és tételt, amelyre a probléma bizonyítási részéhez lesz szükség. Amellett, hogy az axiómák és tételek ismerete közvetlenül segít a vizsgán a probléma megoldása során, ezek ismétlése lehetővé teszi a szilárd geometriai ismeretek rendszerezését és általánosítását, vagyis egyfajta holisztikus kialakítást. kép ebből a tudásból.

Szóval mit kell tanulnod?

Módokon síkot állít be a térben, a vonalak és síkok kölcsönös elrendezése a térben.

párhuzamos egyenesek és síkokűrben.

Definíciók, jelek és tulajdonságok merőleges egyenesek és síkokűrben.

Miután megismételte az elméletet, elkezdheti a problémák megoldásának módszereit mérlegelni. Az 1C: Tutor tanfolyam tartalma: videó előadások elmélettel, szimulátorok lépésről lépésre problémamegoldással, önvizsgálati tesztek, interaktív modellek, amelyek lehetővé teszik a 10. és 11. évfolyamos tanulók számára, hogy vizuálisan mérlegeljék a sztereometriai problémák megoldásának módszereit, beleértve a példákat is. problémákról USE 2017.

Javasoljuk a problémák megoldását a következő sorrendben:

1. Szögek a térben (metsző egyenesek között, egyenes és sík között, síkok között);
2. Távolságok a térben (két pont között, pont és egyenes között, pont és sík között, ferde vonalak között);
3. A poliéderek megoldása, vagyis az élek és lapok közötti szögek, az élek közötti távolságok, felületek, térfogatok megtalálása a feladatfelvetésben megadott elemek szerint;
4. Poliéderszelvények - metszetek készítésének módszerei (például a nyomok módszere), valamint a metszet megalkotása után kapott poliéderek metszeteinek és térfogatainak megkeresésére (például a merőleges vetítés tulajdonságainak és a térfogatok módszerének felhasználásával).

Az összes ilyen típusú probléma megoldására többféle módszer létezik:

klasszikus (definíciók és jellemzők alapján);

vetítési módszer;

pontcsere módszere;

kötet módszer.

Ezeket a módszereket ismerni és alkalmazni kell, hiszen vannak olyan feladatok, amiket egyik módszerrel elég nehéz, másikkal sokkal könnyebben megoldani.

A sztereometriai feladatok megoldása során a vektor-koordináta módszer gyakran hatékonyabbnak bizonyul, mint a klasszikus módszer. A klasszikus problémamegoldási módszer megköveteli a sztereometria axiómáinak és tételeinek kiváló ismeretét, gyakorlati alkalmazásának képességét, építsenek rajzokat a térbeli testekről, és redukálják a sztereometrikus problémát egy planimetrikus láncra. A klasszikus módszer általában gyorsabban vezet a kívánt eredményhez, mint a vektor-koordináta módszer, de megköveteli a gondolkodás bizonyos rugalmasságát. A vektor-koordináta módszer kész képletek és algoritmusok halmaza, de hosszadalmasabb számításokat igényel; Egyes feladatokhoz azonban pl szögek keresése a térben, előnyösebb, mint a klasszikus.

Sok jelentkező nem tud megbirkózni a sztereometrikus feladattal fejletlen térbeli képzelet. Ebben az esetben javasoljuk az interaktív szimulátorok használatát a térbeli testek dinamikus modelljeivel az önképzéshez. az 1C: Tutor portálon (a használatukra való átálláshoz regisztrálnia kell): velük dolgozva nemcsak „lépésről lépésre” tudja „felépíteni” a probléma megoldását, hanem láthatja az összes szakaszt rajz konstrukció különböző szögekből egy háromdimenziós modellen.

Ugyanezen dinamikus rajzok segítségével javasoljuk, hogy tanulja meg a poliéderek metszeteit. Amellett, hogy a modell automatikusan ellenőrzi a konstrukció helyességét, Ön saját maga is meg tudja győződni arról, hogy a metszet különböző oldalairól megvizsgálja, hogy helyesen vagy helytelenül van-e megépítve, és ha hibás, akkor pontosan mi a hiba. Egy metszet papírra építése, ceruza és vonalzó használata természetesen nem ad ilyen lehetőségeket. Nézzen meg egy példát egy piramis szakaszának sík mentén történő megépítésére egy ilyen modell segítségével (Kattintson a képre a szimulátor eléréséhez):

Az utolsó megfontolandó kérdés az keresztmetszeti területek vagy térfogatok megtalálása poliéderszakasz felépítése után kapott. Vannak olyan megközelítések és tételek is, amelyek általános esetben lehetővé teszik jelentősen csökkenti a munkaerőköltségeket megoldást keresni és választ kapni. Az „1C: Tutor” tanfolyamon bemutatjuk ezeket a technikákat.

Ha követte tanácsainkat, foglalkozott az itt felvetett problémákkal, és megfelelő számú feladatot megoldott, akkor valószínűleg szinte készen áll a szilárd geometria feladatának megoldására a 2018-as matematika profilvizsgán. Ezután már csak a vizsgáig kell „formában” tartani magát, azaz megoldani, megoldani és megoldani a problémákat, fejleszteni tudását. alkalmazza a tanult technikákat és módszereket különböző helyzetekben. Sok szerencsét!

Gyakorold rendszeresen a problémamegoldást

Az 1C: Tutor portálon való tanulás megkezdéséhez elegendő.
Tudsz:

• csináld magad és ingyen oktatási anyagok felhasználásával, beleértve egy oktatóvideó készletet, lépésről lépésre szimulátorokat és online teszteket mindegyikhez HASZNÁLAT témát;
• hatékonyabb (figyelembe véve a tanulók észlelésének sajátosságait) eszközt használjon: passz, amelyen részletesen elemzik a matematikai USE problémák megoldásának elméletét és módszereit.

2017-ben webinárium-sorozatot tartottunk a racionális egyenletek és egyenlőtlenségek témakörében. A webinárium felvételei azon felhasználók számára lesznek elérhetőek, akik a teljes tanfolyamra előfizettek 9900₽ 7900 ₽. Tesztre megteheted vásároljon hozzáférést egy hónapra 990 ₽ áron

Itt kulcs kifejezések hogy a keresőrobotok jobban megtalálják tippjeinket:
Hogyan kell megoldani a 14. feladatot HASZNÁLAT vizsga, geometriai feladatok, problémamegoldás, sztereometria, problémamegoldó módszerek, szimulátorok, videó, KIM USE 2017, felkészítés az USE-ra, matematikus profilja, profilszint matematika, feladat megoldása ferde háromszög prizmán, lapok, kölcsönösen merőleges, közös él, síkok , pontok, él egyenlő, oldalfelület, feladatok megoldása poliéder metszetén, merőleges metszet, alakzat térfogatának kiszámítása, derékszögű prizma alapjában fekszik, egyenlőség és hasonlóság jelei háromszögek, példák geometriai USE feladatok megoldására, szakaszszámítás, speciális szintű matematikai feladatok, metszetmódszerek alkalmazása, területi feladatok megoldása, HASZNÁLJON feladatokat 2017 sztereometriából, egységes államvizsgára felkészítés, 11. évfolyamosok, 2018-ban műszaki egyetemre való felvétel.