Egyenlőtlenségek online megoldása

Az egyenlőtlenségek megoldása előtt meg kell érteni, hogyan oldják meg az egyenleteket.

Nem számít, hogy az egyenlőtlenség szigorú () vagy nem szigorú (≤, ≥), első lépésként meg kell oldani az egyenletet úgy, hogy az egyenlőtlenség jelét egyenlőséggel (=) helyettesítjük.

Magyarázza el, mit jelent egy egyenlőtlenség megoldása?

Az egyenletek tanulmányozása után a hallgatónak a következő kép van a fejében: meg kell találnia a változó olyan értékeit, amelyekre az egyenlet mindkét része ugyanazt az értéket veszi fel. Más szóval, keresse meg az összes pontot, ahol az egyenlőség érvényesül. Minden helyes!

Amikor egyenlőtlenségekről beszélünk, az azt jelenti, hogy megtaláljuk azokat az intervallumokat (szegmenseket), amelyeken az egyenlőtlenség érvényes. Ha az egyenlőtlenségben két változó van, akkor a megoldás már nem intervallumok, hanem a sík egyes területei lesznek. Találd ki, mi lesz a három változós egyenlőtlenség megoldása?

Hogyan lehet megoldani az egyenlőtlenségeket?

Az intervallumok módszere (más néven intervallumok módszere) az egyenlőtlenségek megoldásának univerzális módjának tekinthető, amely abból áll, hogy meghatározzuk mindazon intervallumokat, amelyeken belül az adott egyenlőtlenség teljesül.

Anélkül, hogy kitérnénk az egyenlőtlenség típusára, ebben az esetben nem ez a lényeg, meg kell oldani a megfelelő egyenletet és meg kell határozni a gyökereit, majd ezeket a megoldásokat meg kell jelölni a numerikus tengelyen.

Hogyan lehet helyesen felírni egy egyenlőtlenség megoldását?

Ha meghatározta az egyenlőtlenség megoldásának intervallumait, magát a megoldást kell helyesen kiírnia. Van egy fontos árnyalat - az intervallumok határai benne vannak a megoldásban?

Itt minden egyszerű. Ha az egyenlet megoldása kielégíti az ODZ-t és az egyenlőtlenség nem szigorú, akkor az intervallum határa benne van az egyenlőtlenség megoldásában. Különben nem.

Minden egyes intervallumot figyelembe véve az egyenlőtlenség megoldása lehet maga az intervallum, vagy egy félintervallum (amikor az egyik határa kielégíti az egyenlőtlenséget), vagy egy szegmens - egy intervallum a határaival együtt.

Fontos pont

Ne gondolja, hogy csak az intervallumok, félintervallumok és szegmensek jelenthetik a megoldást egy egyenlőtlenségre. Nem, a megoldásban egyedi pontok is szerepelhetnek.

Például az |x|≤0 egyenlőtlenségnek csak egy megoldása van - a 0 pont.

És az egyenlőtlenség |x|

Mire való az egyenlőtlenség-kalkulátor?

Az egyenlőtlenség-kalkulátor megadja a helyes végső választ. Ebben az esetben a legtöbb esetben egy numerikus tengely vagy sík illusztrációja szerepel. Láthatja, hogy az intervallumok határai benne vannak-e a megoldásban vagy sem - a pontok kitöltve vagy áttörve jelennek meg.

Az online egyenlőtlenség-kalkulátornak köszönhetően ellenőrizheti, hogy helyesen találta-e meg az egyenlet gyökereit, jelölte-e meg a számegyenesen, és ellenőrizte-e az egyenlőtlenség feltételeit az intervallumokon (és határokon)?

Ha az Ön válasza eltér a kalkulátor válaszától, akkor feltétlenül ellenőrizze a megoldást, és azonosítsa az elkövetett hibát.

Ma, barátaim, nem lesz takony és érzelem. Ehelyett a 8-9. osztályos algebratanfolyam egyik legfélelmetesebb ellenfelével küldöm harcba további kérdések nélkül.

Igen, mindent jól értettél: modulusos egyenlőtlenségekről beszélünk. Négy alapvető technikát fogunk megvizsgálni, amelyek segítségével megtanulhatja a problémák körülbelül 90%-ának megoldását. Mi van a többi 10%-kal? Nos, róluk egy külön leckében lesz szó. :)

Mielőtt azonban bármilyen trükköt elemeznék, szeretnék felidézni két tényt, amelyeket már tudnod kell. Ellenkező esetben azt kockáztatja, hogy egyáltalán nem érti a mai óra anyagát.

Amit már tudnod kell

Evidence kapitány arra utal, hogy az egyenlőtlenségek modulusos megoldásához két dolgot kell tudnia:

1. Hogyan oldják meg az egyenlőtlenségeket?
2. Mi az a modul.

Kezdjük a második ponttal.

Modul meghatározása

Itt minden egyszerű. Két definíció létezik: algebrai és grafikus. Kezdjük az algebrával:

Meghatározás. A $x$ szám modulja vagy maga a szám, ha nem negatív, vagy a vele ellentétes szám, ha az eredeti $x$ továbbra is negatív.

Így van írva:

\[\left| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(igazítás) \jobbra.\]

Egyszerűen fogalmazva, a modulus „egy mínusz nélküli szám”. És ez a kettősség (valahol nem kell semmit csinálni az eredeti számmal, de valahol el kell távolítani a mínuszokat), és minden nehézség a kezdő hallgatók számára.

Van egy geometriai meghatározás is. Hasznos is tudni, de csak bonyolult és néhány speciális esetben hivatkozunk rá, ahol a geometriai megközelítés kényelmesebb, mint az algebrai (spoiler: ma nem).

Meghatározás. A valós egyenesen legyen az $a$ pont. Ezután a $\left| modul x-a \right|$ az $x$ pont és az $a$ pont távolsága ezen az egyenesen.

Ha rajzolsz egy képet, valami ilyesmit kapsz:

Így vagy úgy, kulcstulajdonsága azonnal következik a modul definíciójából: egy szám modulusa mindig nem negatív érték. Ez a tény egy vörös szál lesz, amely végigfut az egész mai történetünkön.

Az egyenlőtlenségek megoldása. Térköz módszer

Most foglalkozzunk az egyenlőtlenségekkel. Nagyon sok van belőlük, de most az a feladatunk, hogy legalább a legegyszerűbbet meg tudjuk oldani. Azokat, amelyeket lineáris egyenlőtlenségekre redukálunk, valamint az intervallumok módszerére.

Két nagy oktatóanyagom van ebben a témában (mellesleg, nagyon-nagyon hasznos - javaslom a tanulmányozást):

1. Az egyenlőtlenségek intervallummódszere (különösen nézze meg a videót);
2. A töredék-racionális egyenlőtlenségek nagyon terjedelmes lecke, de utána már egyáltalán nem marad kérdésed.

Ha mindezt tudod, ha az "egyenlőtlenségből térjünk át az egyenletre" kifejezés nem késztet homályosan arra, hogy falhoz öld magad, akkor készen állsz: üdv a pokolban az óra fő témájában. :)

1. "A modul kisebb, mint a függvény" alakú egyenlőtlenségek

Ez az egyik leggyakrabban előforduló feladat a modulokkal kapcsolatban. Meg kell oldani a forma egyenlőtlenségét:

\[\left| f\right| \ltg\]

Bármi működhet $f$ és $g$ függvényként, de általában polinomok. Példák az ilyen egyenlőtlenségekre:

\[\begin(align) & \left| 2x+3\jobbra| \ltx+7; \\ & \left| ((x)^(2))+2x-3 \jobbra|+3\left(x+1 \jobbra) \lt 0; \\ & \left| ((x)^(2))-2\bal| x \jobbra|-3 \jobbra| \lt 2. \\\end(igazítás)\]

Mindegyik szó szerint egy sorban van megoldva a séma szerint:

\[\left| f\right| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(igazítás) \jó jó)\]

Könnyen belátható, hogy megszabadulunk a modultól, de helyette kettős egyenlőtlenséget (vagy ami ugyanaz, két egyenlőtlenség rendszerét) kapunk. De ez az átmenet abszolút minden lehetséges problémát figyelembe vesz: ha a modul alatti szám pozitív, a módszer működik; ha negatív, akkor is működik; és még akkor is működik a módszer, ha a $f$ vagy $g$ helyett a legelégtelenebb függvény van.

Természetesen felmerül a kérdés: nem könnyebb? Sajnos nem lehet. Ez a modul lényege.

De elég a filozofálásból. Oldjunk meg pár problémát:

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| 2x+3\jobbra| \ltx+7\]

Megoldás. Tehát van egy klasszikus „a modul kisebb, mint” formájú egyenlőtlenségünk – nincs is mit átalakítani. A következő algoritmus szerint dolgozunk:

\[\begin(align) & \left| f\right| \lt g\Jobbra -g \lt f \lt g; \\ & \left| 2x+3\jobbra| \lt x+7\Jobbra -\balra(x+7 \jobbra) \lt 2x+3 \lt x+7 \\\vége(igazítás)\]

Ne rohanjon kinyitni a zárójeleket, amelyeket „mínusz” előz meg: nagyon valószínű, hogy a sietség miatt támadó hibát követ el.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(igazítás) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(igazítás) \jobbra.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(igazítás) \jobbra.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(igazítás) \jobbra.\]

A probléma két elemi egyenlőtlenségre redukálódott. Megoldásaikat párhuzamos valós egyeneseken jegyezzük meg:

Sokak kereszteződése

Ezeknek a halmazoknak a metszéspontja lesz a válasz.

Válasz: $x\in \left(-\frac(10)(3);4 \right)$

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| ((x)^(2))+2x-3 \jobbra|+3\left(x+1 \jobbra) \lt 0\]

Megoldás. Ez a feladat egy kicsit nehezebb. Először is elkülönítjük a modult a második tag jobbra mozgatásával:

\[\left| ((x)^(2))+2x-3 \jobbra| \lt -3\left(x+1 \right)\]

Nyilvánvalóan ismét van egy „a modul kevesebb” alakú egyenlőtlenségünk, így a már ismert algoritmus szerint megszabadulunk a modultól:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Most figyelem: valaki azt fogja mondani, hogy egy kicsit perverz vagyok ezekkel a zárójelekkel. De még egyszer emlékeztetem önöket, hogy a legfontosabb célunk az helyesen oldja meg az egyenlőtlenséget, és kapja meg a választ. Később, amikor tökéletesen elsajátítottad az ebben a leckében leírtakat, tetszés szerint elferdítheti magát: zárójeleket nyithat, mínuszokat adhat hozzá stb.

Kezdetnek pedig megszabadulunk a bal oldali dupla mínusztól:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\left(x+1\right)\]

Most nyissuk meg a kettős egyenlőtlenség összes zárójelét:

Térjünk át a kettős egyenlőtlenségre. Ezúttal a számítások komolyabbak lesznek:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(igazítás) \jobbra.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( igazítás)\jobbra.\]

Mindkét egyenlőtlenség négyzet alakú, és az intervallum módszerrel oldjuk meg (ezért mondom: ha nem tudod, mi az, jobb, ha még nem veszel fel modulokat). Áttérünk az első egyenlőtlenség egyenletére:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\vége(igazítás)\]

Amint látható, a kimenet egy hiányos másodfokú egyenlet, amelyet elemileg megoldottak. Most foglalkozzunk a rendszer második egyenlőtlenségével. Itt alkalmazni kell Vieta tételét:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\vége(igazítás)\]

A kapott számokat két párhuzamos egyenesre jelöljük (külön az első egyenlőtlenséghez és külön a másodikhoz):

Ismételten, mivel egyenlőtlenségrendszert oldunk meg, az árnyékolt halmazok metszéspontja érdekel minket: $x\in \left(-5;-2 \right)$. Ez a válasz.

Válasz: $x\in \left(-5;-2 \right)$

Azt hiszem, ezek után a példák után a megoldási séma nagyon világos:

1. Izolálja le a modult úgy, hogy az összes többi tagot az egyenlőtlenség ellenkező oldalára helyezi. Így egy $\left| alakú egyenlőtlenséget kapunk f\right| \ltg$.
2. Oldja meg ezt az egyenlőtlenséget úgy, hogy a fent leírt módon megszabadul a modultól. Valamikor el kell térni a kettős egyenlőtlenségtől a két független kifejezésből álló rendszer felé, amelyek mindegyike már külön-külön is megoldható.
3. Végül már csak e két független kifejezés megoldását kell keresztezni – és ennyi, megkapjuk a végső választ.

Hasonló algoritmus létezik a következő típusú egyenlőtlenségekre, amikor a modulus nagyobb, mint a függvény. Van azonban egy-két komoly "de". Most ezekről a „de”-ekről fogunk beszélni.

2. "A modul nagyobb, mint a függvény" alakú egyenlőtlenségek

Így néznek ki:

\[\left| f\right| \gt g\]

Hasonló az előzőhöz? Úgy tűnik. Ennek ellenére az ilyen feladatokat teljesen más módon oldják meg. Formálisan a séma a következő:

\[\left| f\right| \gt g\Jobbra \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(igazítás) \jobbra.\]

Más szóval, két esetet vizsgálunk:

1. Először egyszerűen figyelmen kívül hagyjuk a modult - megoldjuk a szokásos egyenlőtlenséget;
2. Ekkor tulajdonképpen megnyitjuk a mínuszjelű modult, majd az egyenlőtlenség mindkét részét megszorozzuk -1-gyel, előjellel.

Ebben az esetben a lehetőségeket szögletes zárójellel kombinálják, pl. Két követelmény kombinációja van.

Figyeld még egyszer: nem egy rendszer áll előttünk, hanem egy aggregátum, tehát a válaszban a halmazokat kombinálják, nem metszik. Ez alapvető különbség az előző bekezdéshez képest!

Általánosságban elmondható, hogy sok diák nagyon zavart a szakszervezetekkel és a kereszteződésekkel, ezért nézzük meg ezt a kérdést egyszer s mindenkorra:

• A "∪" egy összefűzési jel. Valójában ez egy stilizált "U" betű, amely az angol nyelvből érkezett hozzánk, és az "Union" rövidítése, azaz „Egyesületek”.
• A "∩" a kereszteződés jele. Ez a baromság nem jött sehonnan, hanem csak a "∪" ellenzékeként jelent meg.

Hogy még könnyebb legyen az emlékezet, csak adjon hozzá lábakat ezekhez a jelekhez, hogy szemüveget készítsen (csak most ne vádoljon a kábítószer-függőség és az alkoholizmus népszerűsítésével: ha komolyan tanulja ezt a leckét, akkor már kábítószer-függő):

Oroszra lefordítva ez a következőket jelenti: az unió (gyűjtemény) mindkét halmazból tartalmaz elemeket, ezért nem kevesebb, mint mindegyik; de a metszéspont (rendszer) csak azokat az elemeket tartalmazza, amelyek az első halmazban és a másodikban is szerepelnek. Ezért a halmazok metszéspontja soha nem nagyobb, mint a forráshalmazok metszéspontja.

Szóval világosabb lett? Az nagyszerű. Térjünk át a gyakorlásra.

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| 3x+1 \jobbra| \gt 5-4x\]

Megoldás. A séma szerint járunk el:

\[\left| 3x+1 \jobbra| \gt 5-4x\Jobbra \balra[ \begin(igazítás) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \jobbra) \\\vége(igazítás) \ jobb.\]

Megoldjuk az egyes népesedési egyenlőtlenségeket:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(igazítás) \jobbra.\]

\[\left[ \begin(igazítás) & x \gt 4/7\ \\ & x \gt 6 \\ \end(igazítás) \jobbra.\]

Minden kapott halmazt megjelölünk a számegyenesen, majd egyesítjük őket:

A halmazok egyesülése

Nyilvánvalóan a válasz $x\in \left(\frac(4)(7);+\infty \right)$

Válasz: $x\in \left(\frac(4)(7);+\infty \right)$

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| ((x)^(2))+2x-3 \jobbra| \gtx\]

Megoldás. Jól? Nem, mindegy. Egy modulusos egyenlőtlenségből két egyenlőtlenség halmazába megyünk át:

\[\left| ((x)^(2))+2x-3 \jobbra| \gt x\Jobbra \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(igazítás) \jobbra.\]

Minden egyenlőtlenséget megoldunk. Sajnos ott nem lesznek túl jók a gyökerek:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\vége(igazítás)\]

A második egyenlőtlenségben van egy kis játék is:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\vége(igazítás)\]

Most meg kell jelölnünk ezeket a számokat két tengelyen - egy tengelyen minden egyenlőtlenséghez. A pontokat azonban megfelelő sorrendben kell megjelölnie: minél nagyobb a szám, annál jobban eltolódik a pont jobbra.

És itt várunk a beállításra. Ha minden világos a $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ számokkal (az első szám számlálójában szereplő kifejezések tört kisebb, mint a második számlálójában szereplő tagok, így az összeg is kisebb, a $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt) számokkal (21))(2)$ szintén nem lesz nehézség (pozitív szám nyilván inkább negatív), de az utolsó párral nem minden olyan egyszerű. Melyik a nagyobb: $\frac(-3+\sqrt(21))(2)$ vagy $\frac(-1+\sqrt(13))(2)$? A kérdésre adott választól függ a pontok elrendezése a számegyeneseken, sőt, a válasz is.

Tehát hasonlítsuk össze:

\[\begin(mátrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(mátrix)\]

Elszigeteltük a gyökeret, nem negatív számokat kaptunk az egyenlőtlenség mindkét oldalán, így jogunk van mindkét oldalt négyzetre emelni:

\[\begin(mátrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(mátrix)\]

Szerintem nem ötlet, hogy $4\sqrt(13) \gt 3$, tehát $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, végül a pontok a tengelyeken a következőképpen lesznek elrendezve:

Csúnya gyökerek esete

Hadd emlékeztesselek arra, hogy egy halmazt oldunk meg, így a válasz az egyesülés lesz, nem pedig az árnyékolt halmazok metszéspontja.

Válasz: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

Amint látja, sémánk kiválóan működik egyszerű és nagyon nehéz feladatok esetén is. Az egyetlen „gyenge pont” ebben a megközelítésben az, hogy helyesen kell összehasonlítani az irracionális számokat (és hidd el: ezek nem csak gyökök). De külön (és nagyon komoly) leckét szentelünk az összehasonlítás kérdéseinek. És továbbmegyünk.

3. Egyenlőtlenségek a nem negatív "farokkal"

Elérkeztünk tehát a legérdekesebbhez. Ezek a formai egyenlőtlenségek:

\[\left| f\right| \gt\left| g\right|\]

Általánosságban elmondható, hogy az algoritmus, amelyről most beszélni fogunk, csak a modulra igaz. Minden olyan egyenlőtlenségben működik, ahol a bal és a jobb oldalon garantáltan nem negatív kifejezések vannak:

Mi a teendő ezekkel a feladatokkal? Csak ne feledd:

A nem negatív farkú egyenlőtlenségekben mindkét oldal bármely természetes hatalomra emelhető. További korlátozások nem lesznek.

Először is érdekelni fogunk a négyzetesítésben - modulokat és gyökereket éget:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\vége(igazítás)\]

Csak ne keverje össze ezt a négyzet gyökerének felvételével:

\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]

Számtalan hibát követtek el, amikor egy hallgató elfelejtett modult telepíteni! De ez egy teljesen más történet (ezek mintha irracionális egyenletek volna), ezért ebbe most nem megyünk bele. Inkább oldjunk meg néhány problémát:

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| x+2 \right|\ge \left| 1-2x \right|\]

Megoldás. Két dolgot azonnal észreveszünk:

1. Ez egy nem szigorú egyenlőtlenség. A számegyenes pontjai ki lesznek lyukasztva.
2. Az egyenlőtlenség mindkét oldala nyilvánvalóan nem negatív (ez a modul tulajdonsága: $\left| f\left(x \right) \right|\ge 0$).

Ezért az egyenlőtlenség mindkét oldalát négyzetre emelhetjük, hogy megszabaduljunk a modulustól és megoldjuk a problémát a szokásos intervallum módszerrel:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\vége(igazítás)\]

Utolsó lépésben csaltam egy kicsit: a modulus paritásával megváltoztattam a tagok sorrendjét (valójában a $1-2x$ kifejezést -1-gyel szoroztam).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ jobb)\jobb)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Intervallum módszerrel oldjuk meg. Térjünk át az egyenlőtlenségről az egyenletre:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\vége(igazítás)\]

A talált gyökereket a számegyenesen jelöljük. Még egyszer: minden pont árnyékolt, mert az eredeti egyenlőtlenség nem szigorú!

Megszabadulni a modul jelétől

Hadd emlékeztesselek a különösen makacsokra: az előjeleket az utolsó egyenlőtlenségből vesszük, amelyet az egyenletre való továbblépés előtt írtunk le. És ugyanabban az egyenlőtlenségben átfestjük a szükséges területeket. Esetünkben ez $\left(x-3 \right)\left(3x+1 \right)\le 0$.

Rendben, most mindennek vége. Probléma megoldódott.

Válasz: $x\in \left[ -\frac(1)(3);3 \right]$.

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \jobbra|\]

Megoldás. Mindent ugyanúgy csinálunk. Nem kommentálok - nézd csak meg a műveletek sorrendjét.

Nézzük négyzetre:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \jobbra| \jobbra))^(2))\le ((\left(\left) ((x)^(2))+3x+4 \jobbra| \jobbra))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \jobbra))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ jobb))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \jobbra)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(igazítás)\]

Távolsági módszer:

\[\begin(igazítás) & \left(-2x-3 \right)\left(2(x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Jobbra nyíl x=-1,5; \\ & 2((x)^(2))+4x+5=0\Jobbra D=16-40 \lt 0\Jobbra \varnothing . \\\vége(igazítás)\]

Csak egy gyök van a számegyenesen:

A válasz egy egész tartomány

Válasz: $x\in \left[ -1.5;+\infty \right)$.

Egy kis megjegyzés az utolsó feladathoz. Ahogy egyik tanítványom pontosan megjegyezte, ebben az egyenlőtlenségben mindkét részmodul kifejezés nyilvánvalóan pozitív, így a modulus jel elhagyható egészségkárosodás nélkül.

De ez már egy teljesen más gondolkodási szint és más megközelítés - feltételesen nevezhetjük a következmények módszerének. Róla - külön leckében. És most térjünk át a mai lecke utolsó részére, és vegyünk egy univerzális algoritmust, amely mindig működik. Még akkor is, ha minden korábbi megközelítés tehetetlen volt. :)

4. Az opciók számbavételének módja

Mi van, ha ezek a trükkök nem működnek? Ha az egyenlőtlenség nem redukálódik nem-negatív farokra, ha lehetetlen elkülöníteni a modult, ha egyáltalán fájdalom-szomorúság-vágy?

Ezután az összes matematika „nehéztüzérsége” lép színre - a számlálási módszer. Ami a modulussal való egyenlőtlenségeket illeti, ez így néz ki:

1. Írja ki az összes részmodul kifejezést, és egyenlővé tegye őket nullával;
2. Oldja meg a kapott egyenleteket, és jelölje meg a talált gyököket egy számegyenesen;
3. Az egyenes több szakaszra lesz osztva, amelyeken belül minden modulnak van egy rögzített előjele, és ezért egyértelműen bővül;
4. Oldja meg az egyenlőtlenséget minden ilyen szakaszon (a megbízhatóság érdekében külön is figyelembe veheti a 2. bekezdésben kapott határgyököket). Kombinálja az eredményeket - ez lesz a válasz. :)

Nos, hogyan? Gyenge? Könnyen! Csak sokáig. Lássuk a gyakorlatban:

Feladat. Oldja meg az egyenlőtlenséget:

\[\left| x+2 \jobbra| \lt\left| x-1 \right|+x-\frac(3)(2)\]

Megoldás. Ez a baromság nem olyan egyenlőtlenségekre vezethető vissza, mint a $\left| f\right| \lt g$, $\left| f\right| \gt g$ vagy $\left| f\right| \lt\left| g \right|$, úgyhogy folytassuk.

Kiírjuk az almodul kifejezéseket, egyenlővé tesszük őket nullával, és megkeressük a gyökereket:

\[\begin(align) & x+2=0\Jobbra x=-2; \\ & x-1=0\Jobbra x=1. \\\vége(igazítás)\]

Összességében két gyökünk van, amelyek három részre osztják a számsort, amelyeken belül minden modul egyedileg jelenik meg:

A számegyenes felosztása szubmoduláris függvények nullákkal

Tekintsük az egyes szakaszokat külön-külön.

1. Legyen $x \lt -2$. Ekkor mindkét részmodul kifejezés negatív, és az eredeti egyenlőtlenséget a következőképpen írjuk át:

\[\begin(igazítás) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1.5 \\ & x \gt 1.5 \\\end(igazítás)\]

Meglehetősen egyszerű korlátot kaptunk. Vegyük keresztbe azzal az eredeti feltevéssel, hogy $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Nyilvánvaló, hogy a $x$ változó nem lehet egyszerre kisebb, mint −2, de nem lehet nagyobb, mint 1,5. Ezen a területen nincsenek megoldások.

1.1. Nézzük külön a határesetet: $x=-2$. Helyettesítsük be ezt a számot az eredeti egyenlőtlenségbe, és ellenőrizzük: érvényes-e?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \jobbra|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0,5\Jobbra \varnothing . \\\vége(igazítás)\]

Nyilvánvaló, hogy a számítások láncolata rossz egyenlőtlenséghez vezetett. Ezért az eredeti egyenlőtlenség is hamis, és $x=-2$ nem szerepel a válaszban.

2. Most legyen $-2 \lt x \lt 1$. A bal oldali modul már "plusszal" fog megnyílni, de a jobb oldali még mindig "mínuszos". Nekünk van:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1,5 \\ & x+2 \lt -x+1+x-1,5 \\& x \lt - 2.5 \\\end(igazítás)\]

Ismét keresztezzük az eredeti követelményt:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

És ismét a megoldások üres halmaza, mivel nincs olyan szám, amely egyszerre kisebb, mint -2,5 és nagyobb, mint -2.

2.1. És ismét egy speciális eset: $x=1$. Az eredeti egyenlőtlenségbe behelyettesítjük:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \left| 3\jobbra| \lt\left| 0 \jobbra|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\Jobbra \varnothing . \\\vége(igazítás)\]

Az előző „speciális esethez” hasonlóan a $x=1$ szám egyértelműen nem szerepel a válaszban.

3. A sor utolsó darabja: $x \gt 1$. Itt minden modul pluszjellel bővül:

\[\begin(igazítás) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \end(igazítás)\ ]

És ismét metszi a talált halmazt az eredeti megszorítással:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \jobb)\]

Végül! Megtaláltuk az intervallumot, ez lesz a válasz.

Válasz: $x\in \left(4,5;+\infty \right)$

Végül egy megjegyzés, amely megóvhatja Önt a hülye hibáktól a valódi problémák megoldása során:

Az egyenlőtlenségek modulos megoldásai általában folytonos halmazok a számegyenesen - intervallumok és szegmensek. Az elszigetelt pontok sokkal ritkábbak. És még ritkábban fordul elő, hogy a megoldás határai (a szakasz vége) egybeesnek a vizsgált tartomány határával.

Ezért ha a határok (azok a nagyon „speciális esetek”) nem szerepelnek a válaszban, akkor ezektől a határoktól balra-jobbra eső területek szinte biztosan nem fognak szerepelni a válaszban. És fordítva: a határ válaszként lépett be, ami azt jelenti, hogy körülötte néhány terület válasz is lesz.

Ezt tartsa szem előtt, amikor ellenőrzi a megoldásait.

Minél többet ért az ember, annál erősebb a megértés vágya

Aquinói Tamás

Az intervallummódszer lehetővé teszi a modulust tartalmazó bármely egyenlet megoldását. Ennek a módszernek a lényege, hogy a numerikus tengelyt több szakaszra (intervallumra) bontjuk, és a tengelyt a modulokban lévő kifejezések nulláival kell felosztani. Ezután minden egyes eredményül kapott szakaszon bármely részmodul kifejezés pozitív vagy negatív. Ezért mindegyik modul bővíthető mínuszjellel vagy pluszjellel. Ezen műveletek után már csak az összes kapott egyszerű egyenletet kell megoldani a vizsgált intervallumon, és kombinálni a kapott válaszokat.

Tekintsük ezt a módszert egy konkrét példán.

|x + 1| + |2x – 4| – |x + 3| = 2x - 6.

1) Keresse meg a kifejezések nulláit a modulokban! Ehhez egyenlővé tesszük őket nullával, és megoldjuk a kapott egyenleteket.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

2) Rendezd a kapott pontokat a kívánt sorrendbe a koordinátaegyenesen. A teljes tengelyt négy részre osztják.

3) Határozzuk meg az egyes kapott szakaszokon a modulokban lévő kifejezések előjeleit! Ehhez bármilyen számot helyettesítünk bennük a számunkra érdekes intervallumokból. Ha a számítás eredménye pozitív szám, akkor a táblázatba "+"-t írunk, ha pedig negatív, akkor "-"-t. Ezt így lehet ábrázolni:

4) Most mind a négy intervallumon megoldjuk az egyenletet, megnyitva a modulokat a táblázatban szereplő előjelekkel. Tehát vegyük figyelembe az első intervallumot:

I intervallum (-∞; -3). Rajta minden modul "-" jellel nyílik meg. A következő egyenletet kapjuk:

-(x + 1) - (2x - 4) - (-(x + 3)) \u003d 2x - 6. Hasonló kifejezéseket mutatunk be, miután előzőleg kinyitottuk a zárójeleket a kapott egyenletben:

X - 1 - 2x + 4 + x + 3 = 2x - 6

A kapott válasz nem számít bele a figyelembe vett intervallumba, így nem szükséges a végső válaszba beírni.

II intervallum [-3; -egy). Ebben az intervallumban a táblázatban "-", "-", "+" jelek találhatók. Így tárjuk fel az eredeti egyenlet moduljait:

-(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Egyszerűsítse a zárójelek kibontásával:

X - 1 - 2x + 4 - x - 3 \u003d 2x - 6. A kapott egyenletben a következőket mutatjuk be:

x = 6/5. A kapott szám nem tartozik a vizsgált intervallumhoz, tehát nem az eredeti egyenlet gyöke.

III intervallum [-1; 2). Megnyitjuk az eredeti egyenlet moduljait azokkal az előjelekkel, amelyek az ábrán a harmadik oszlopban találhatók. Kapunk:

(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Szabaduljon meg a zárójelektől, mozgassa az x változót tartalmazó kifejezéseket az egyenlet bal oldalára, és az x-et nem tartalmazó kifejezéseket jobbra. . Lesz:

x + 1 - 2x + 4 - x - 3 = 2x - 6

A 2-es szám nem szerepel a figyelembe vett intervallumban.

IV intervallum

Példa megoldva.

3. példa . Oldja meg az egyenlőtlenséget 6 x 2 - | x| - 2 ≤ 0

Megoldás.

Szám x lehet pozitív, negatív vagy nulla. Ezért mindhárom körülményt figyelembe kell vennünk. Mint tudják, ezeket két egyenlőtlenségben veszik figyelembe: x≥ 0 és x < 0. При x≥ 0, egyszerűen átírjuk az eredeti egyenlőtlenségünket úgy, ahogy van, csak modulo jel nélkül:

6x 2 - x - 2 ≤ 0.

Most a második eset: ha x < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6x 2 - (-x) - 2 ≤ 0.

A zárójelek bővítése:

6x 2 + x - 2 ≤ 0.

Így két egyenletrendszert kaptunk:

6x 2 - x - 2 ≤ 0
x ≥ 0

6x 2 + x - 2 ≤ 0
x < 0

Meg kell oldanunk a rendszerekben lévő egyenlőtlenségeket – ami azt jelenti, hogy meg kell találnunk két másodfokú egyenlet gyökerét. Ehhez az egyenlőtlenségek bal oldalát nullával egyenlővé tesszük.

Kezdjük az elsővel:

6x 2 - x - 2 = 0.

Másodfokú egyenlet megoldása – lásd a „Négyfokú egyenlet” részt. Azonnal megnevezzük a választ:

x 1 \u003d -1/2, x 2 = 2/3.

Az első egyenlőtlenségrendszerből azt kapjuk, hogy az eredeti egyenlőtlenség megoldása a teljes számhalmaz -1/2-től 2/3-ig. A megoldások unióját írjuk x ≥ 0:
[-1/2; 2/3].

Most oldjuk meg a második másodfokú egyenletet:

6x 2 + x - 2 = 0.

A gyökerei:

x 1 = -2/3, x 2 = 1/2.

Következtetés: mikor x < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

Kombináljuk a két választ, és kapjuk meg a végső választ: a megoldás a -2/3-tól 2/3-ig terjedő számok teljes halmaza, beleértve ezeket a szélső számokat is.

Válasz: -2/3 ≤ x ≤ 2/3.

Vagy: x ∈ [-2/3; 2/3].

FIGYELEMBE VETT

Pedagógiai Tanács MOU

"Zashizhma középiskola"

1. protokoll

EGYETÉRT

UVR igazgatóhelyettes

_______ /Sidorkina R.L./

JÓVÁHAGY

Iskolaigazgató:

A. P. Konakov

63. sz

Egyenletek és egyenlőtlenségek megoldása modulussal

Kutatás

A program a következőkből állt:

felsőfokú matematika tanár

Sidorkina R.L.

kontra Zashizhemye, 2014

Tartalomjegyzék

Bevezetés………………………………………………………………………3

A legegyszerűbb egyenletek és egyenlőtlenségek a modulussal………………………5

Egyenletek és egyenlőtlenségek grafikus megoldása a modullal………….8

Egyenletek és egyenlőtlenségek megoldásának egyéb módjai a modulussal………10

Következtetés …………………………………………………………………..16

Hivatkozások……………………………………………………………………………………………………………………………………………………………………………………………………………

1. Bevezetés

Az abszolút érték (modulus) fogalma a számok egyik legfontosabb jellemzője mind a valós, mind a komplex számok terén.

Ezt a fogalmat nemcsak az iskolai matematika kurzus különböző szakaszaiban használják széles körben, hanem az egyetemeken tanult felsőfokú matematika, fizika és műszaki tudományok kurzusaiban is. Például a közelítő számítások elméletében egy közelítő szám abszolút és relatív hibájának fogalmát használják. A mechanikában és a geometriában a vektor fogalmát és hosszát (vektor modulusát) tanulmányozzák. A matematikai elemzésben a szám abszolút értékének fogalmát olyan alapfogalmak definíciói tartalmazzák, mint a határérték, a korlátos függvény stb. Az abszolút értékekkel kapcsolatos problémák gyakran előfordulnak matematikai olimpiákon, egyetemi felvételi vizsgákon. és az Egységes Államvizsga. Ezért fontossá vált számunkra, hogy tanulmányozzuk ennek a témának néhány aspektusát.

itthon célja munkánkban az egyenletek és egyenlőtlenségek modulokkal történő megoldására szolgáló különféle módszerek tanulmányozása.

Ezt a célt a következők megoldásával kell elérni feladatokat:

Vizsgálja meg a modul definícióját és néhány tulajdonságát.

Sajátítsa el a modulusos legegyszerűbb egyenletek és egyenlőtlenségek megoldását ekvivalens átmeneteken keresztül

Tekintsünk különféle módszereket egyenletek és egyenlőtlenségek modulusos megoldására.

tárgy tanulmányok bizonyos típusú egyenletek és egyenlőtlenségek modulussal.

Dolog kutatás - különböző módszerek egyenletek és egyenlőtlenségek megoldására egy modullal, nevezetesen: grafikus módszer, geometriai értelmezés módszere, azonosság használata, tétel alkalmazása jelekre, következményre való átmenet módja, intervallumok módszere, pozitív tényezővel való szorzás módszere, modulok bővítésének módja.

A vizsgálat során olyan módszereket alkalmaztak, mint a kérdéskör szakirodalmának tanulmányozása és a gyakorlati módszer.

Munkánk során olyan forrásokat kutattunk, mint:

1. "Big Mathematical Encyclopedia" iskolásoknak és diákoknak;

Matematika. HASZNÁLAT - 2011-2012. Standard vizsgalehetőségek. / Szerk.: A.L. Semenova, I.V. Jascsenko.

Enciklopédia "Ismerem a világot" Matematika;

;

1. 1. A legegyszerűbb egyenletek és modulusos egyenlőtlenségek

A legegyszerűbb egyenletekre hivatkozunk az alábbi egyenértékű átmenetek egyikével megoldott egyenletekre:

Példák a legegyszerűbb egyenletek megoldására.

1. példa Oldjuk meg az egyenletet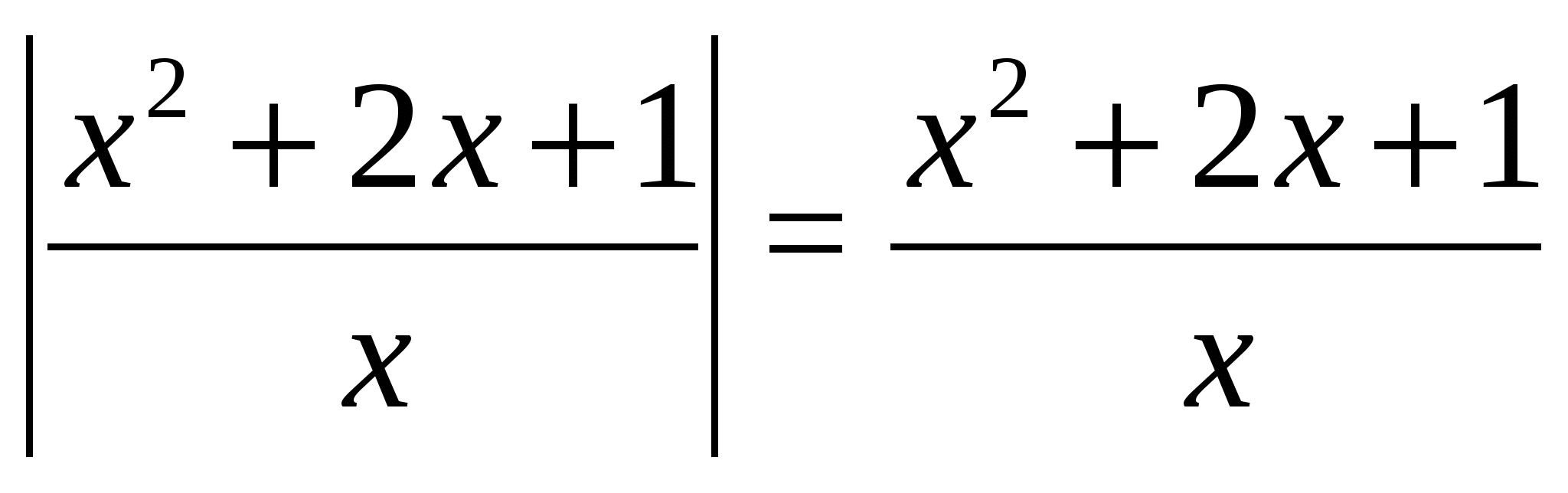
.

Megoldás.

Válasz.
.

2. példa Oldjuk meg az egyenletet.

Megoldás.

Válasz.
.

3. példa Oldjuk meg az egyenletet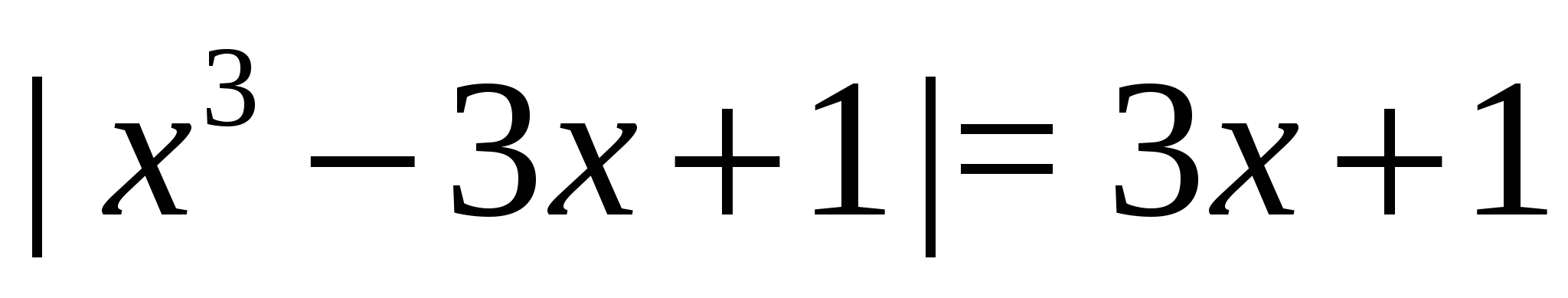
.

Megoldás.

Válasz.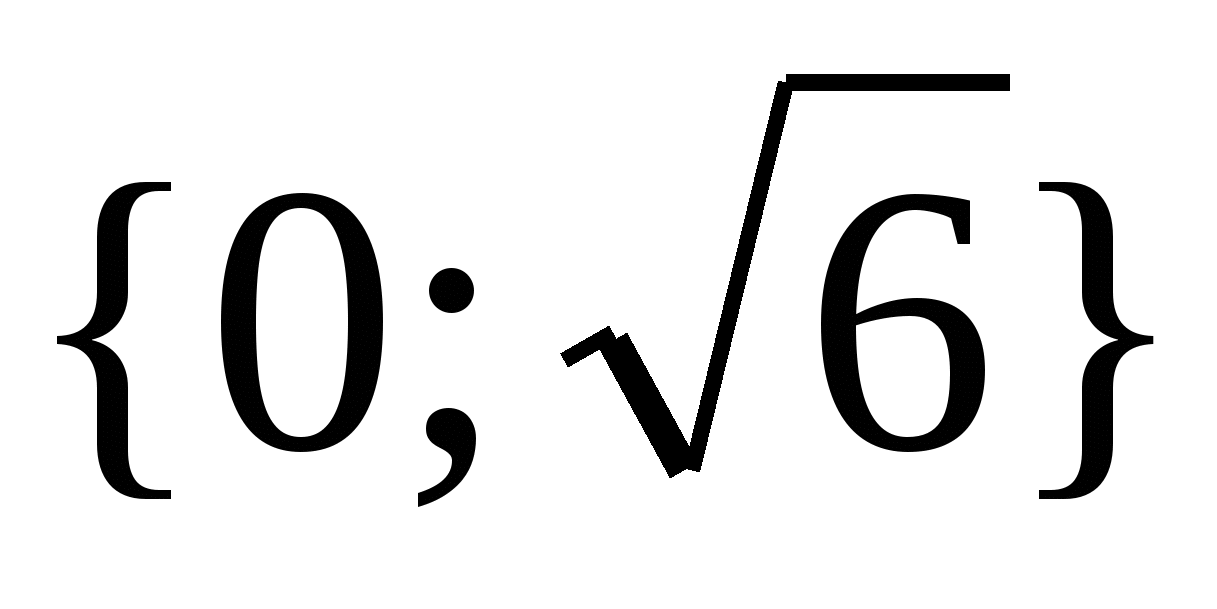
.

Számos egyenletet megoldunk a következő tétel segítségével.

Tétel.4 A modulok összege akkor és csak akkor egyenlő a részmodul mennyiségeinek algebrai összegével, ha minden mennyiségnek van előjele, amellyel belép az algebrai összegbe.

5. példa oldja meg az egyenletet

Megoldás. Mivel , van egy egyenlőségünk az alakban, ahol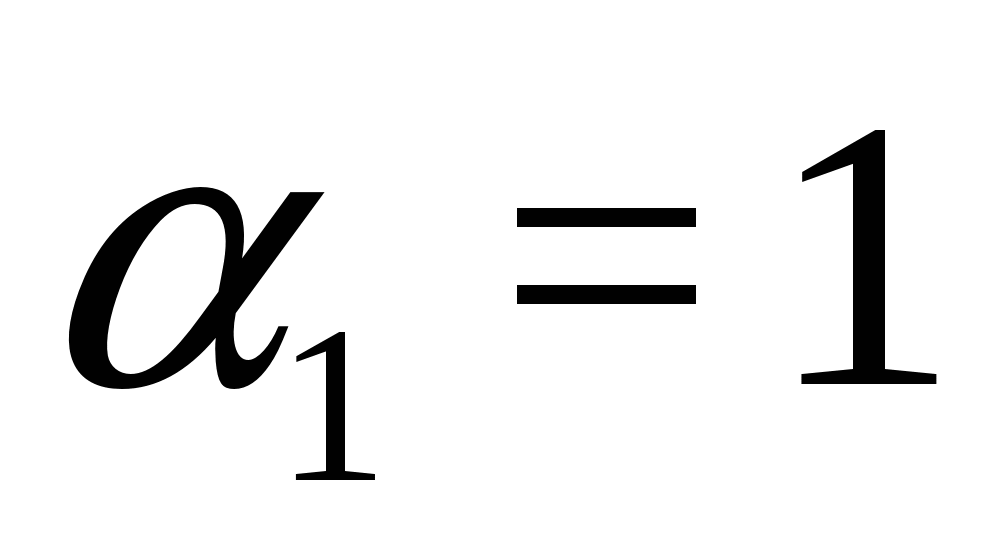
,
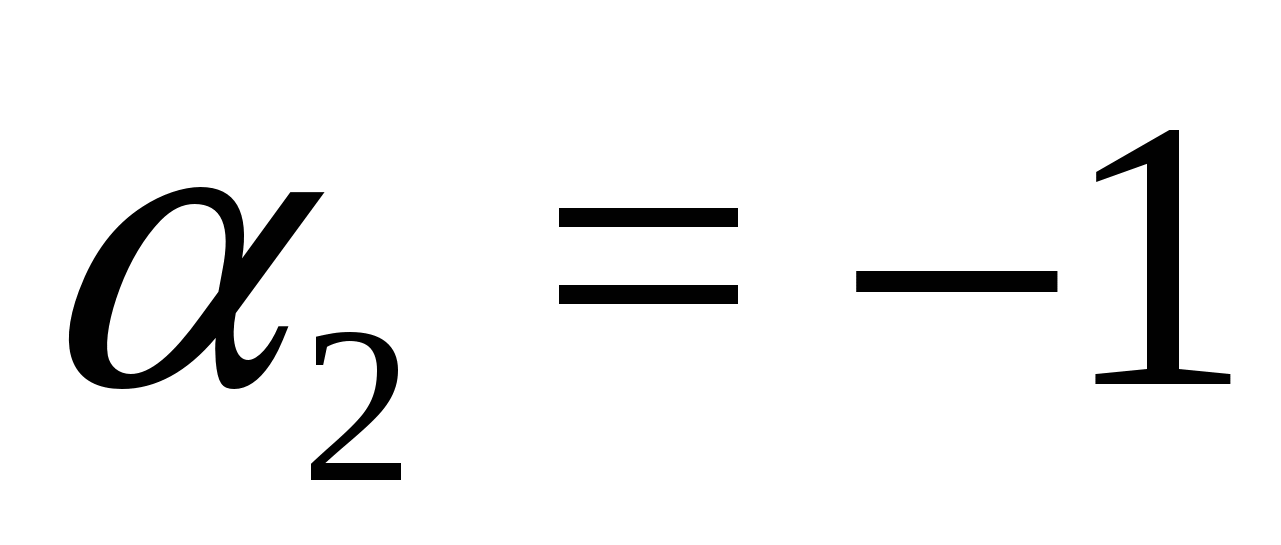. Ezért az eredeti egyenlet ekvivalens a rendszerrel:

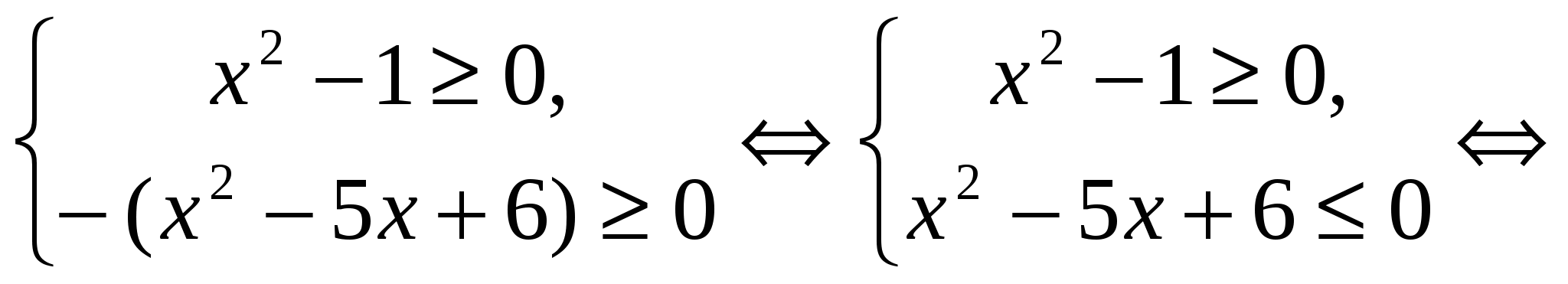
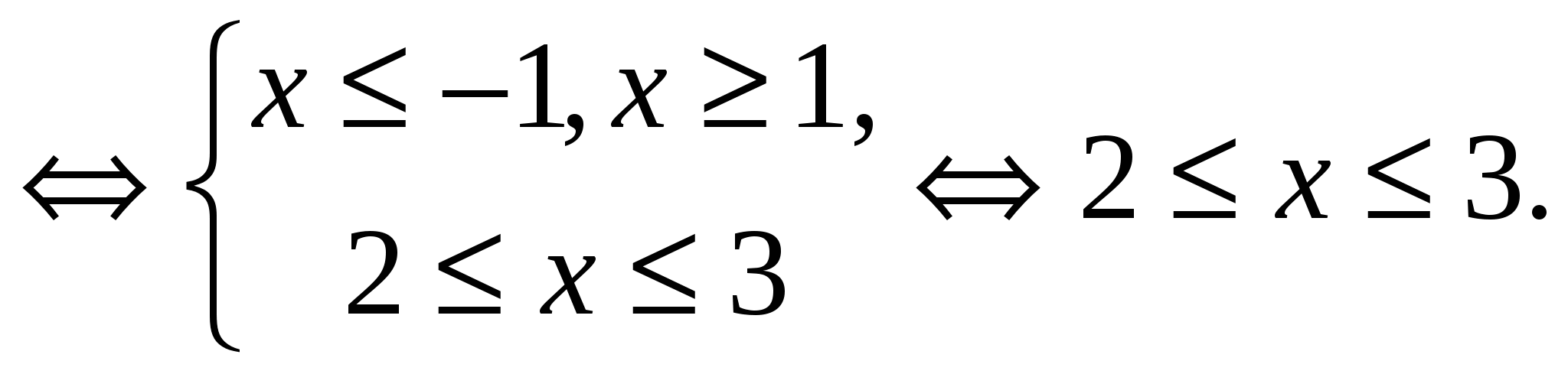
Válasz.
.

Példák a legegyszerűbb egyenlőtlenségek megoldására.

6. példa Oldjuk meg az egyenlőtlenséget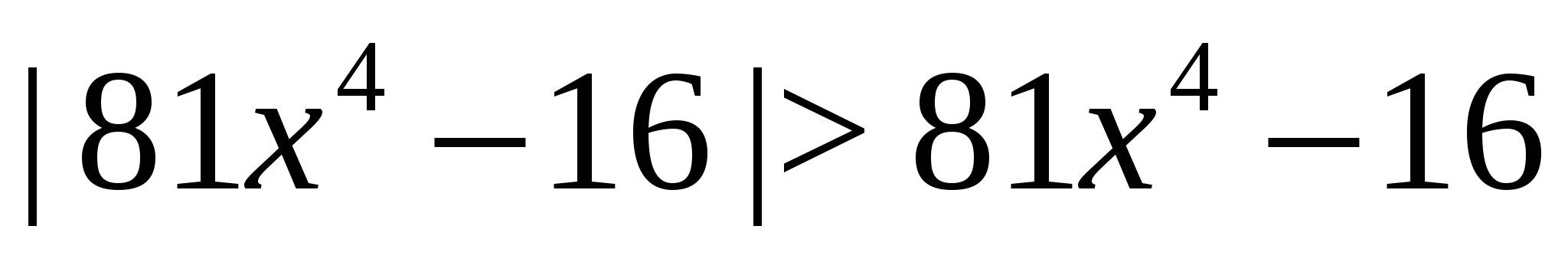
.

Megoldás.

Válasz.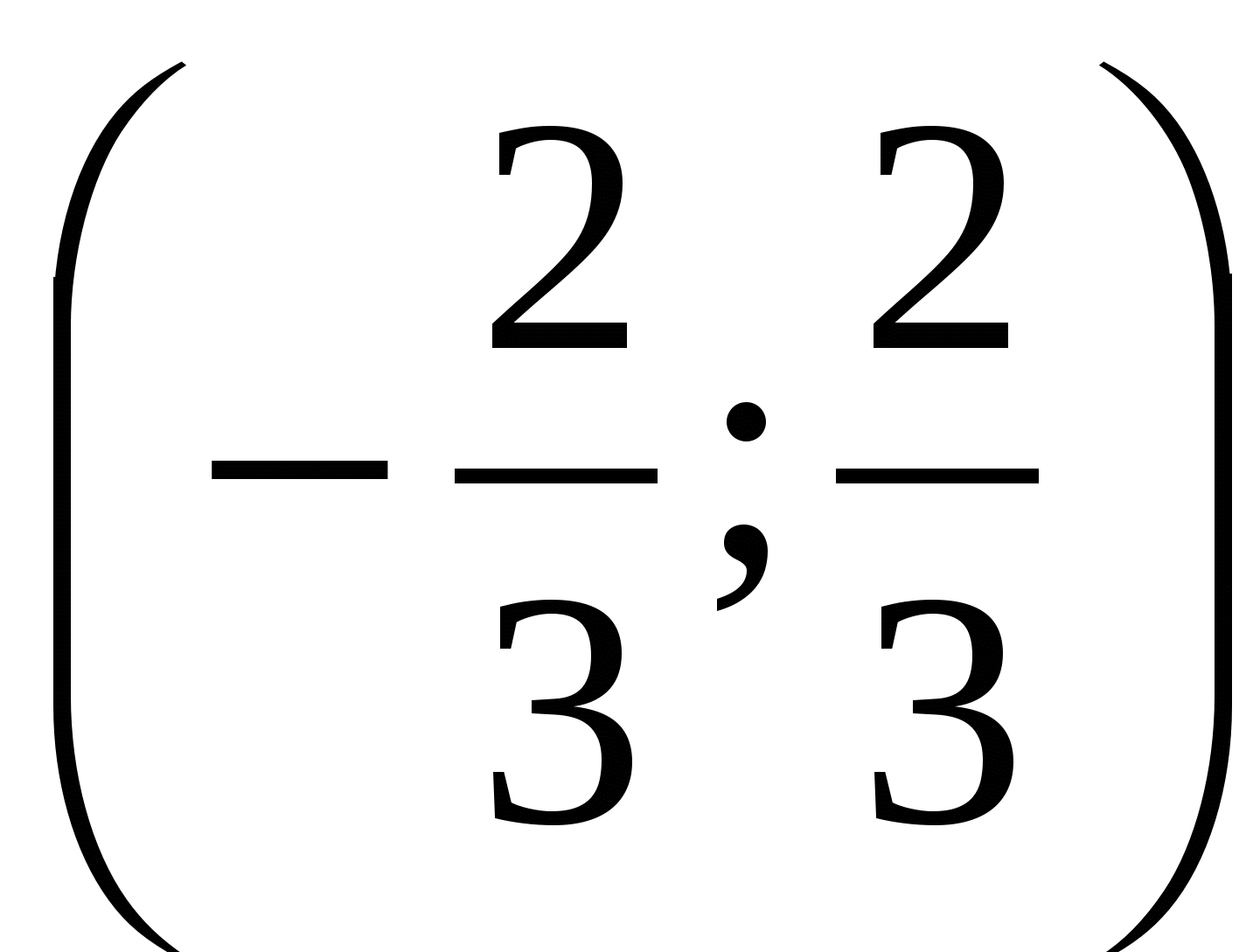
.

7. példa Oldjuk meg az egyenlőtlenséget
.

Megoldás.

Válasz.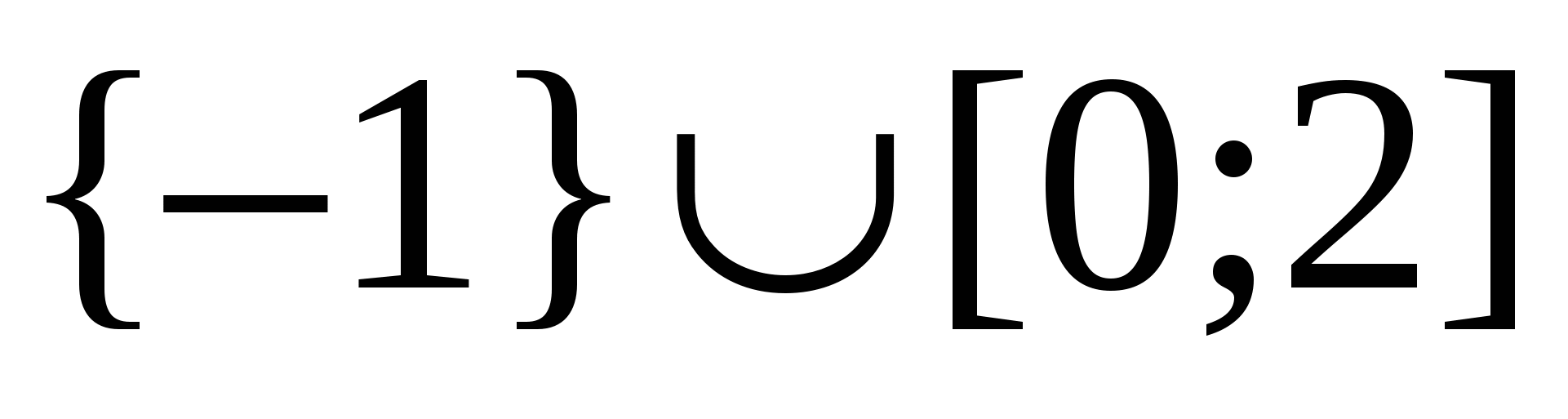
.

Furcsa módon, de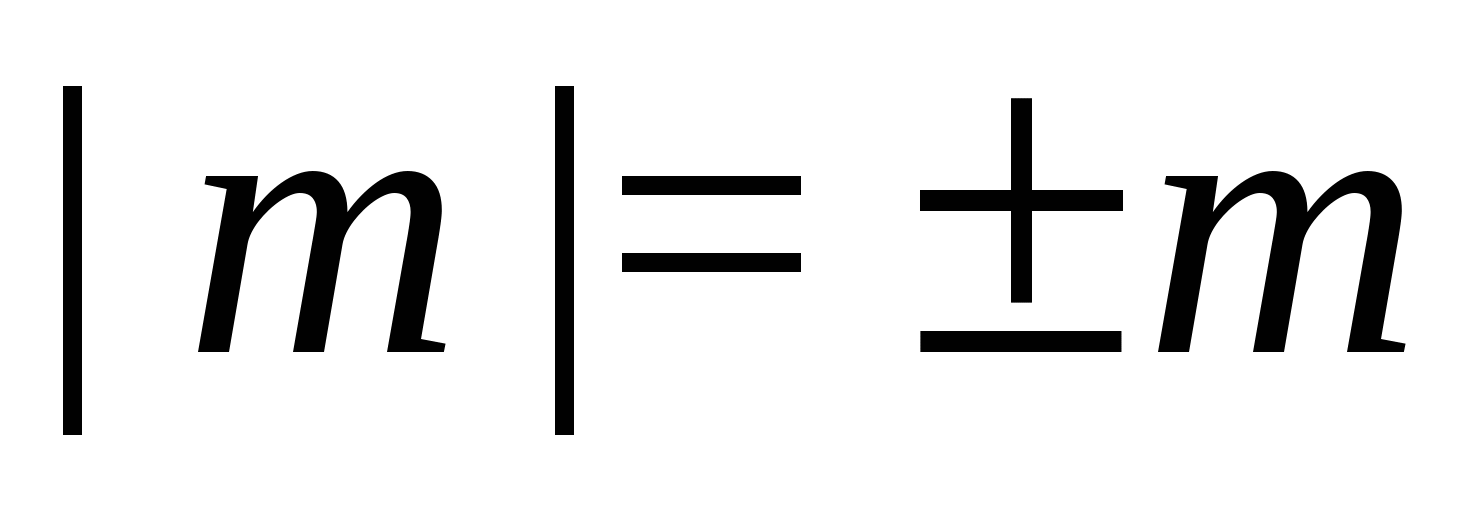
elég ahhoz, hogy bármilyen egyenlőtlenségben megszabaduljunk a modulo jeltől.

8. példa Oldja meg az egyenlőtlenséget

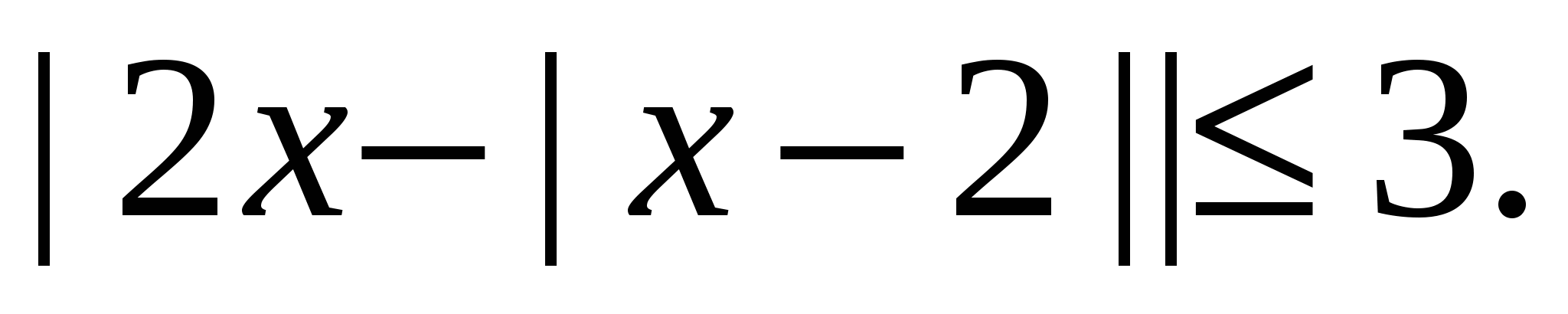
Megoldás.

Válasz.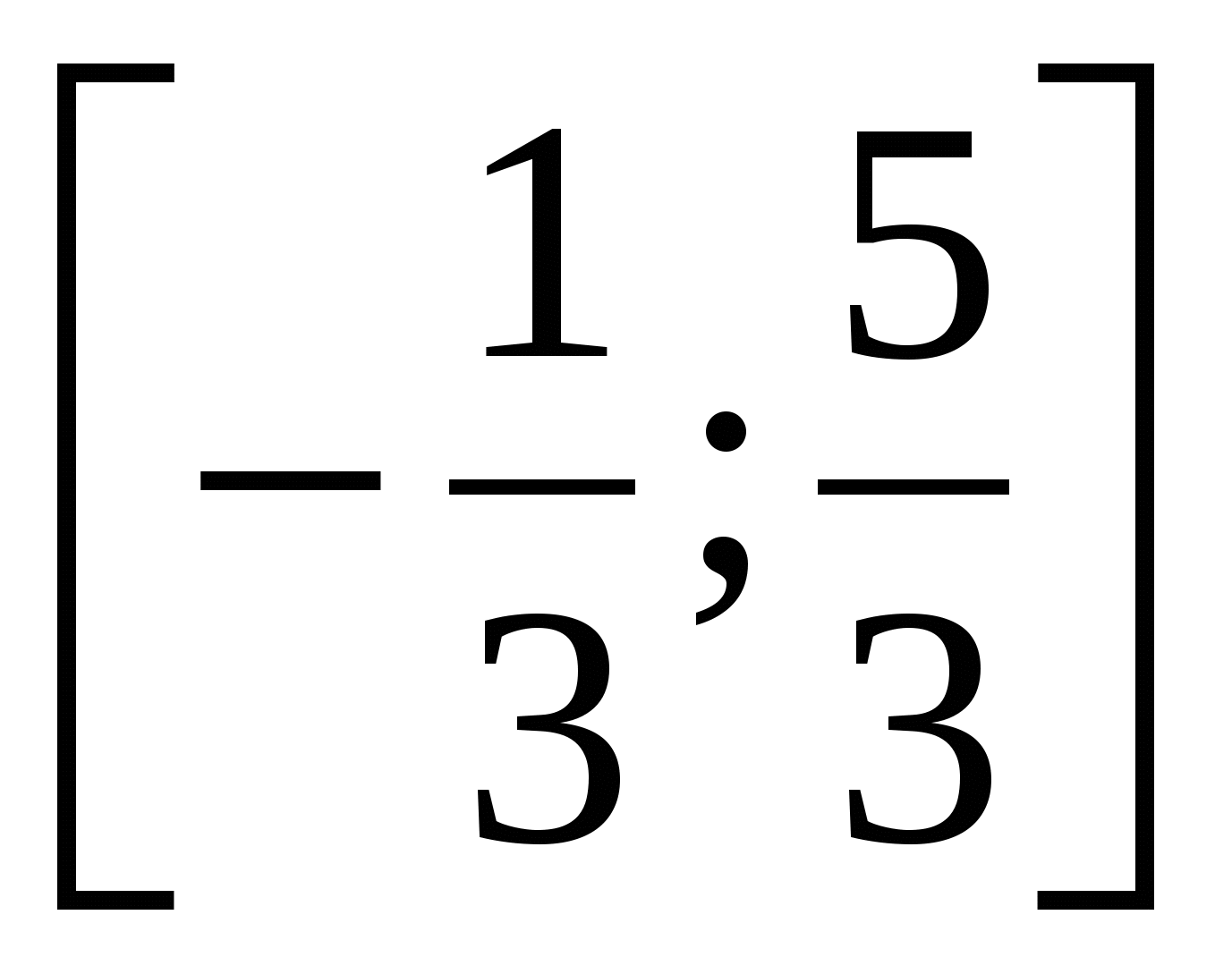
.

3. Egyenletek és modulusos egyenlőtlenségek grafikus megoldása

Az abszolút érték előjelét tartalmazó egyenletek megoldását sokszor sokkal kényelmesebb nem analitikusan, hanem grafikusan megoldani (különösen a paramétereket tartalmazó egyenleteket).

9. példa(C5, USE – 2010)

C5. Minden értékheza jelölje meg az egyenlet megoldásainak számát

Megoldás.Ábrázoljuk a függvényt
. Ehhez válasszon ki egy teljes négyzetet:

Az y függvény grafikonjának metszéspontjainak száma \u003d
vízszintes vonalakkal y = a egyenlő az egyenlet megoldásainak számával.

O válasz: ha < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, majd két megoldás.

Egyenletek és egyenlőtlenségek modulussal történő megoldásának egyéb módjai

• Modulbővítési módszer

Nézzük meg a modulbővítési módszert egy példa segítségével:

10. példa oldja meg az egyenletet

Megoldás. Ez az egyenlet egynél több modult tartalmaz.

A két vagy több modul előjele alatt álló változókat tartalmazó egyenletek megoldásának módja a következő.

1. Keresse meg annak a változónak az értékét, amelynél az egyes modulok eltűnnek: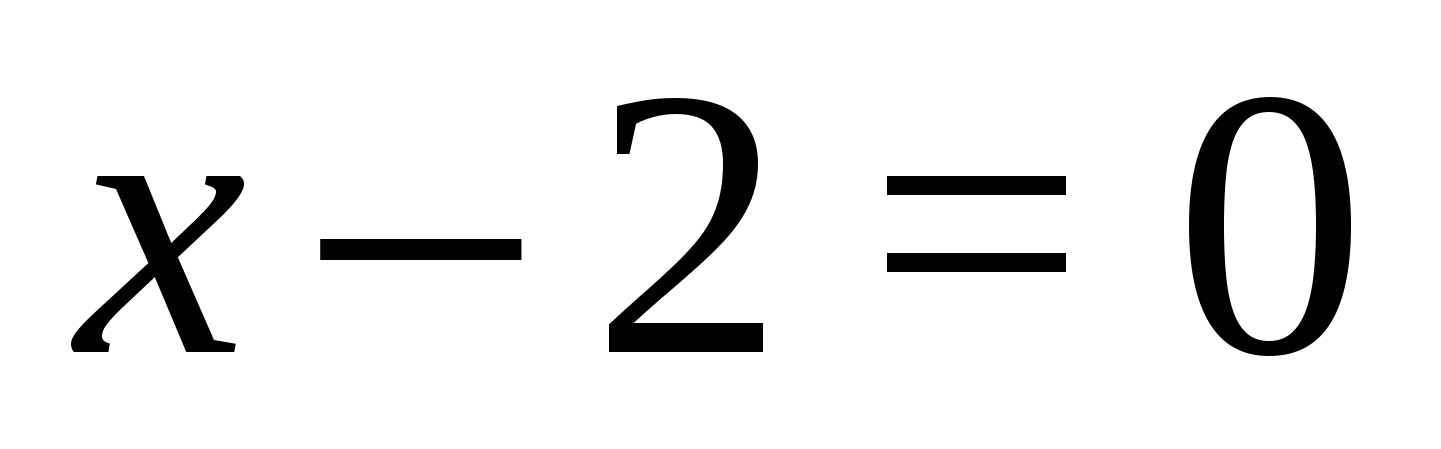
,
;
,
;
,
.

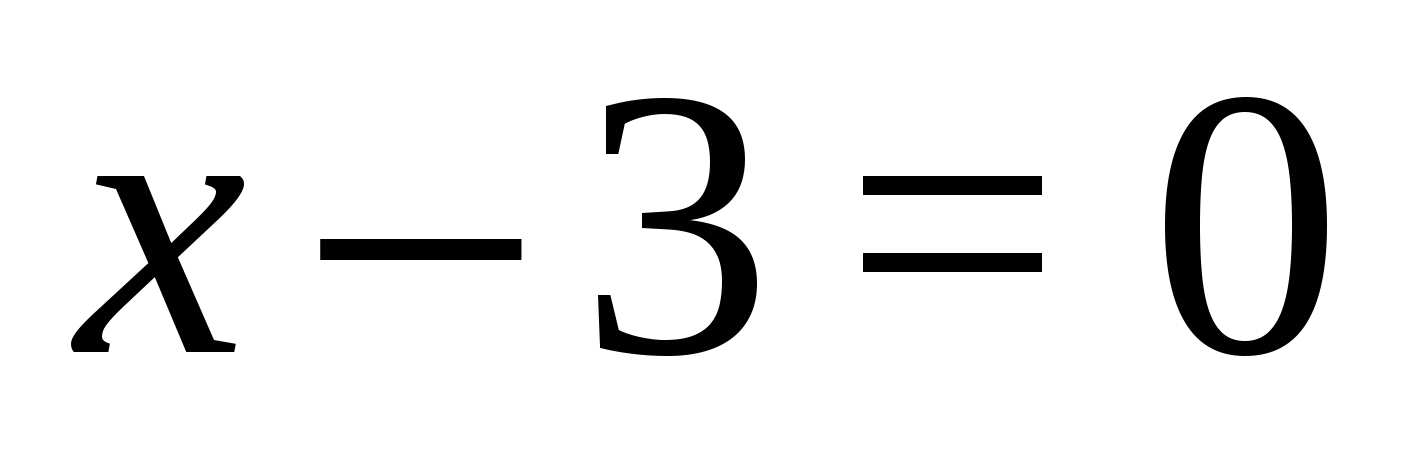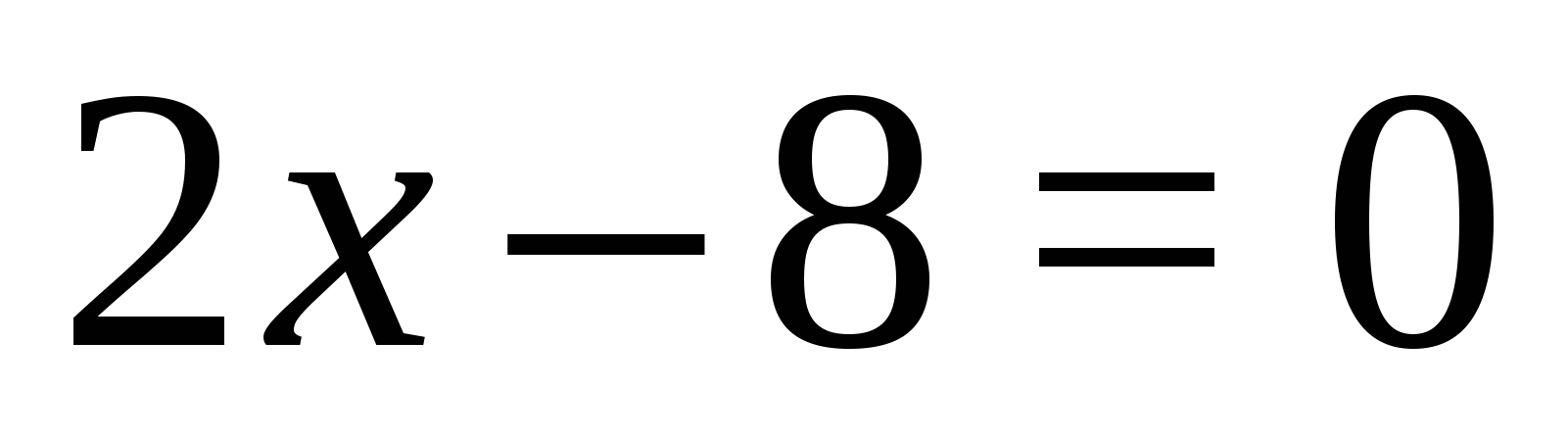2. Jelölje be ezeket a pontokat a számegyenesen!

3. Minden intervallumon figyelembe vesszük az egyenletet, és beállítjuk a modulok alatti kifejezések előjelét.

1) Mikor
vagy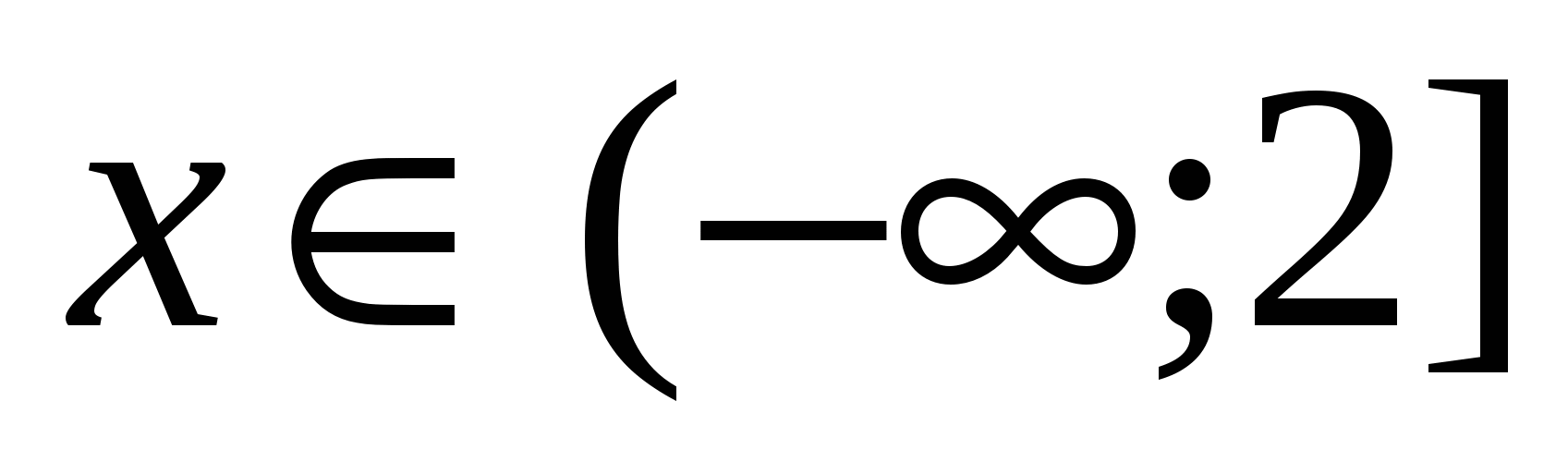
. A modulus alatti egyes kifejezések előjelének meghatározásához ezen az intervallumon elegendő bármilyen értéket felvenni ebből az intervallumból és behelyettesítjük a kifejezésbe. Ha a kapott érték negatív, akkor mindenre ebből az intervallumból a kifejezés negatív lesz; ha a kapott számérték pozitív, akkor minden értékre ebből az intervallumból a kifejezés pozitív lesz.

Vegyük az értéket
a résből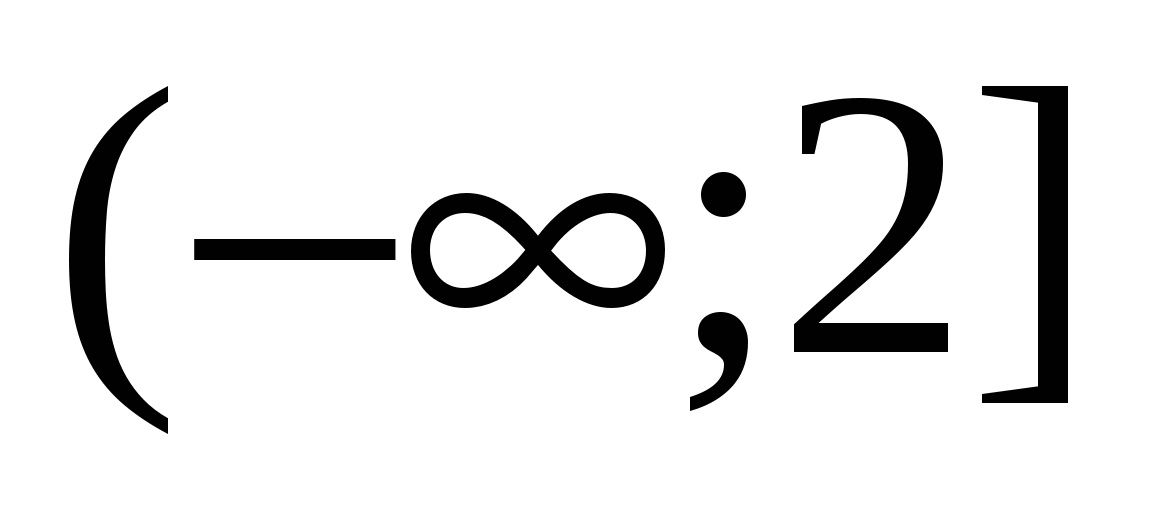
és behelyettesítjük az értékét a kifejezésbe
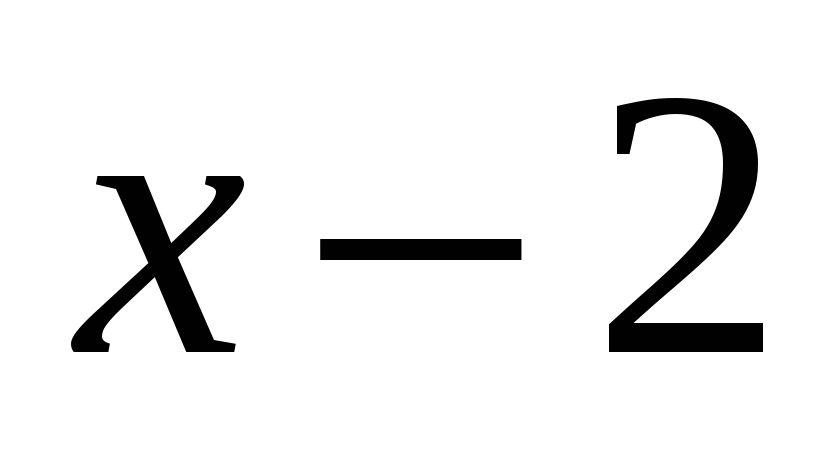, kapunk
, tehát ezen az intervallumon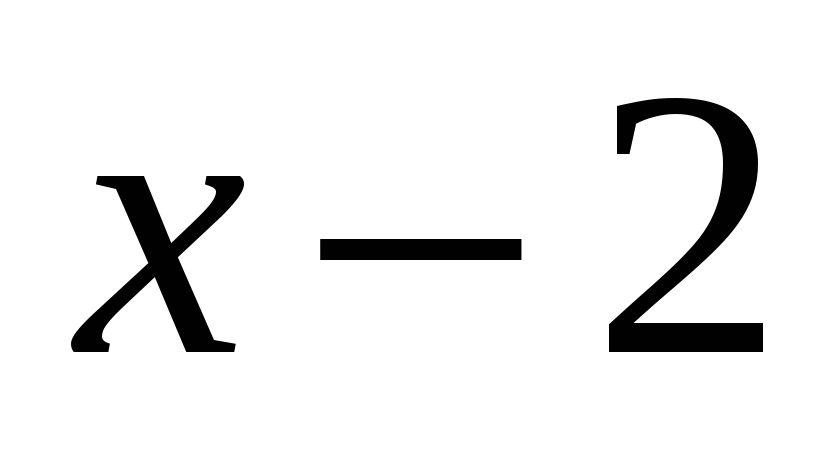
negatív, ezért ``ki" a modul alól "mínuszjellel"" kapjuk:
.

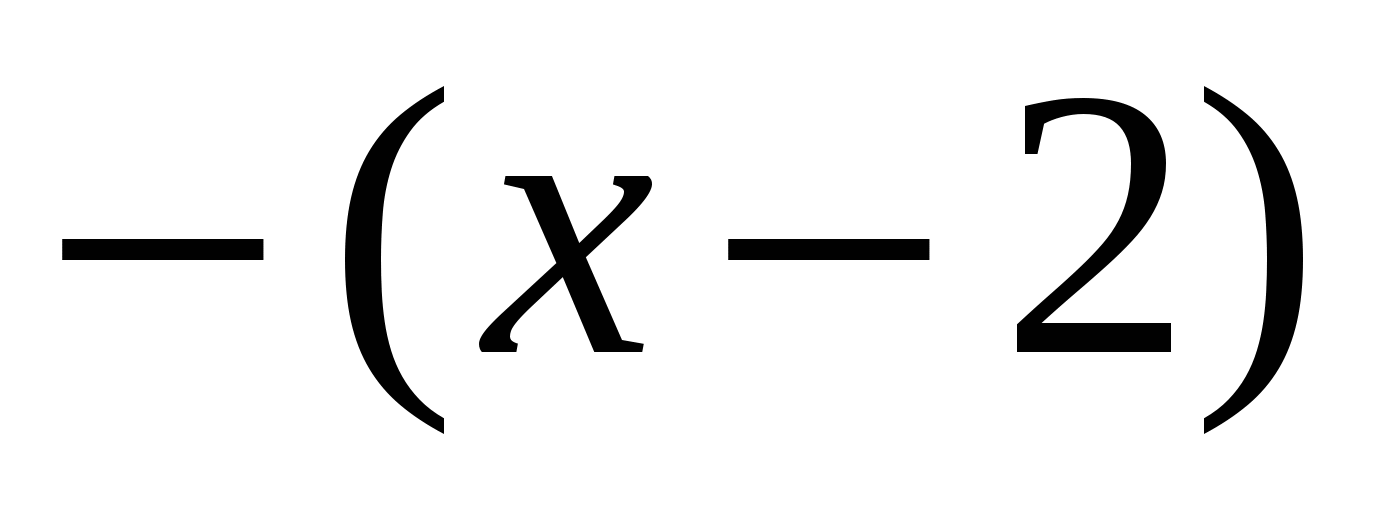Ezzel az értékkel , kifejezés
megkapja az értéket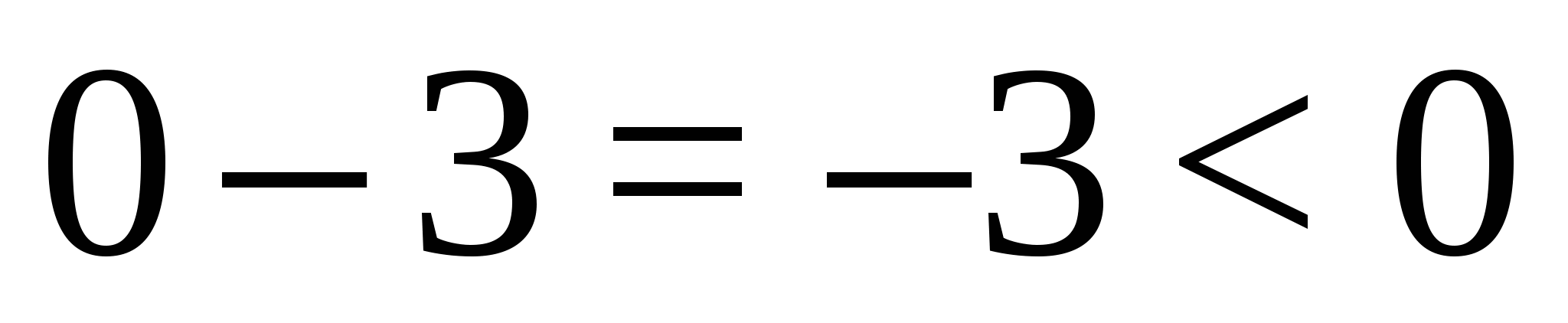
, tehát az intervallumban van
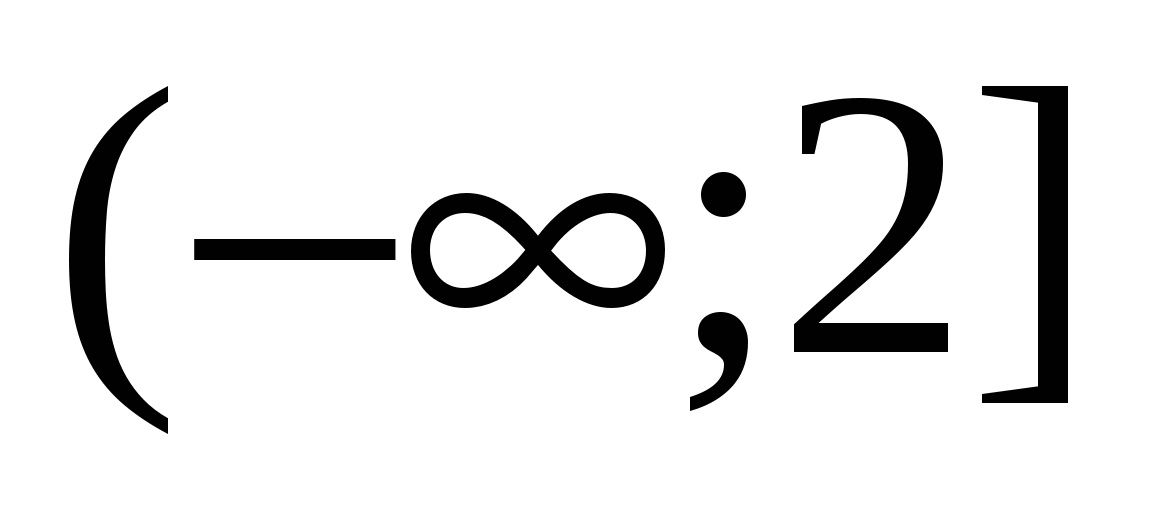elfogadja a negatív értékeket és a ``kihagy""-t is a modulból ``mínusz"' jellel, kapjuk:
.

Kifejezés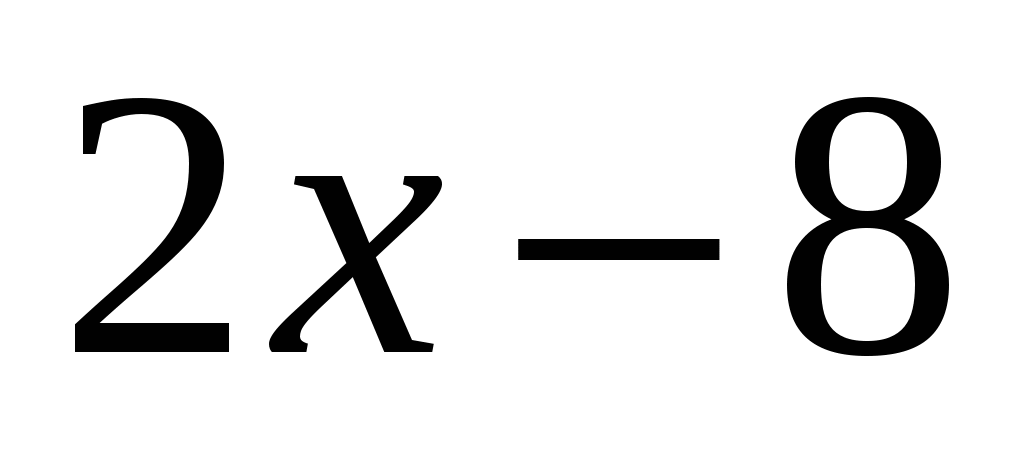
megkapja az értéket
és "mínusz" jellel "kilép" a modulból:
.

Az egyenlet ezen az intervallumon a következőképpen alakul: , megoldva azt találjuk:
.

Nézze meg, hogy ez az érték a tartományban van-e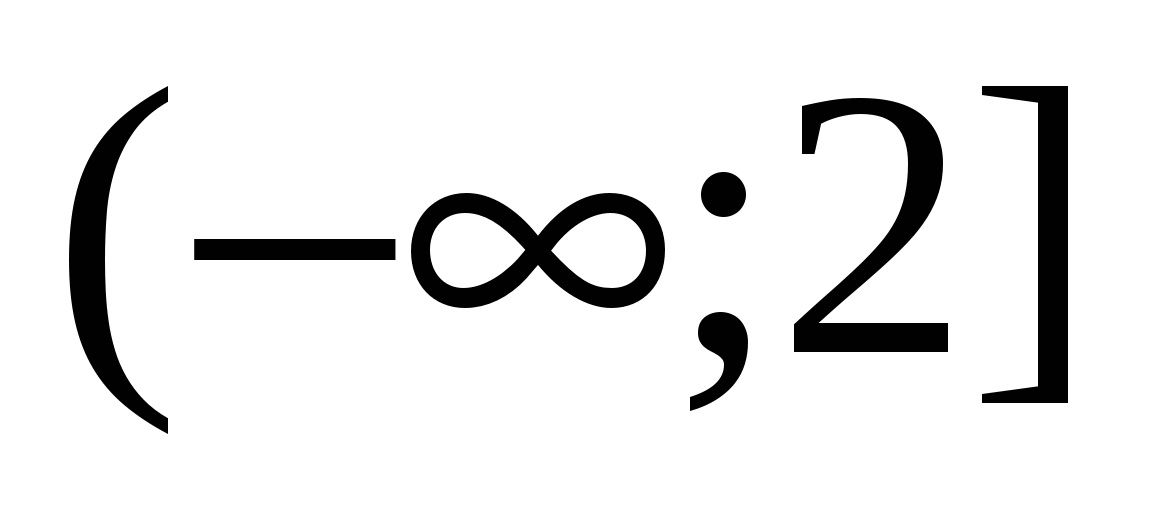
. Kiderült, hogy benne van
az egyenlet gyöke.

2) Mikor
. Válasszon bármilyen értéket ebből az intervallumból. Hadd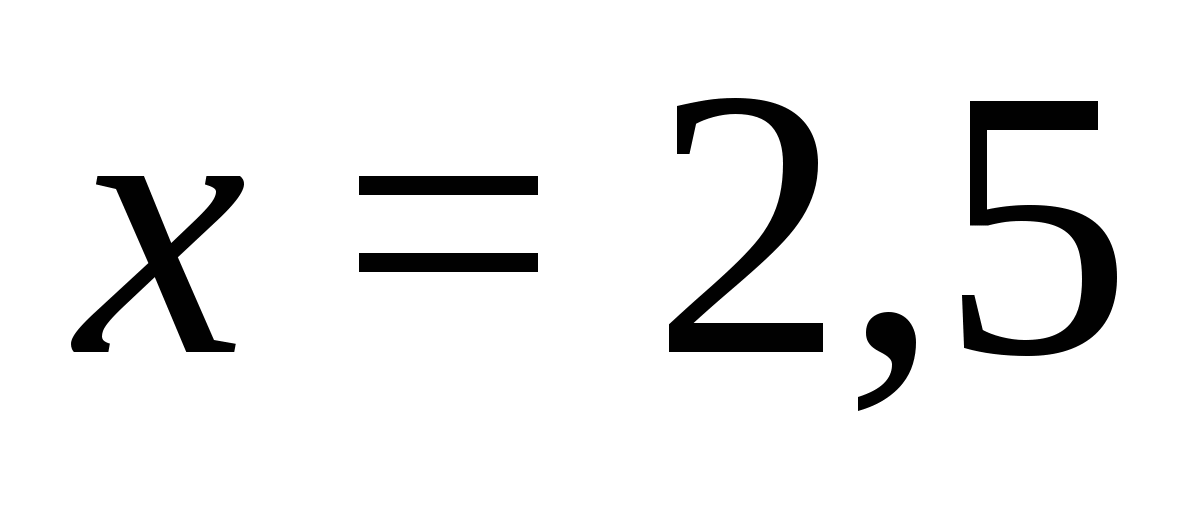
. Ezen az értéken határozzuk meg a modul alatti egyes kifejezések előjelét . Kiderült, hogy a kifejezés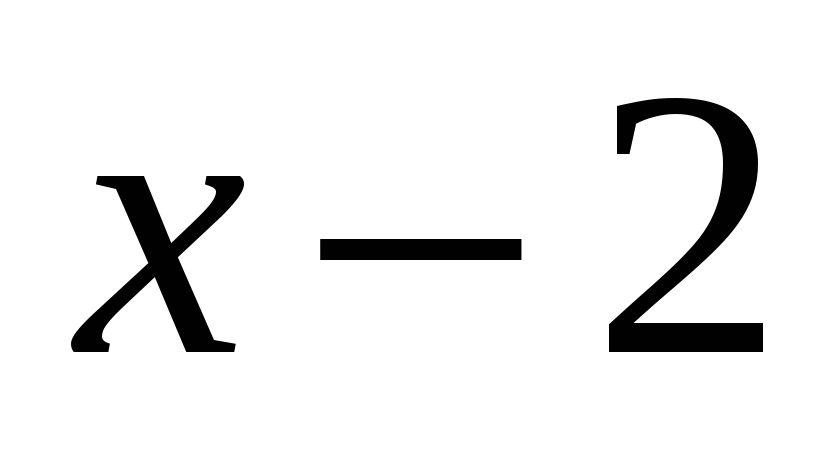
pozitív, a másik kettő pedig negatív.

Ezen az intervallumon az egyenlet a következő formában lesz: . Megoldjuk, megtaláljuk
. Ez az érték nem szerepel a tartományban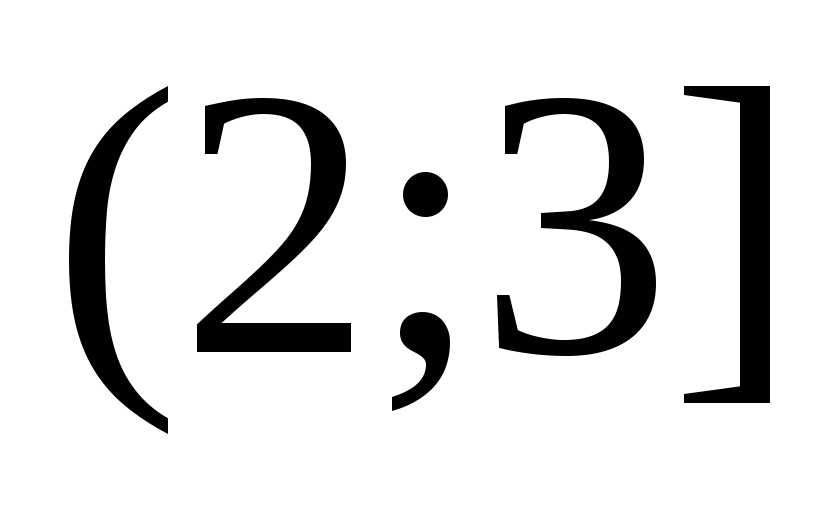
, ami azt jelenti, hogy nem az egyenlet gyöke.

3) Mikor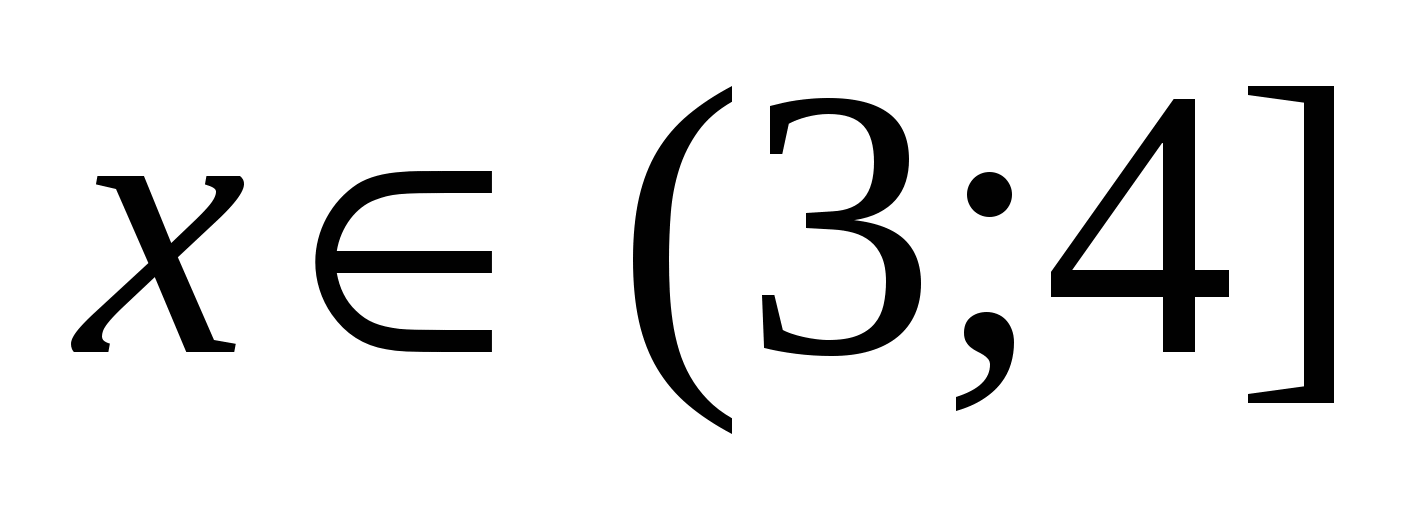
. Válasszon egy tetszőleges értéket ebből az intervallumból mondjuk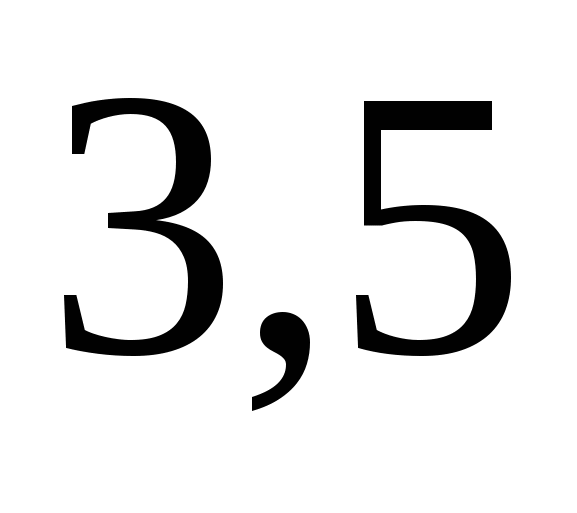
és helyettesítse be az egyes kifejezéseket. Azt találjuk, hogy a kifejezések
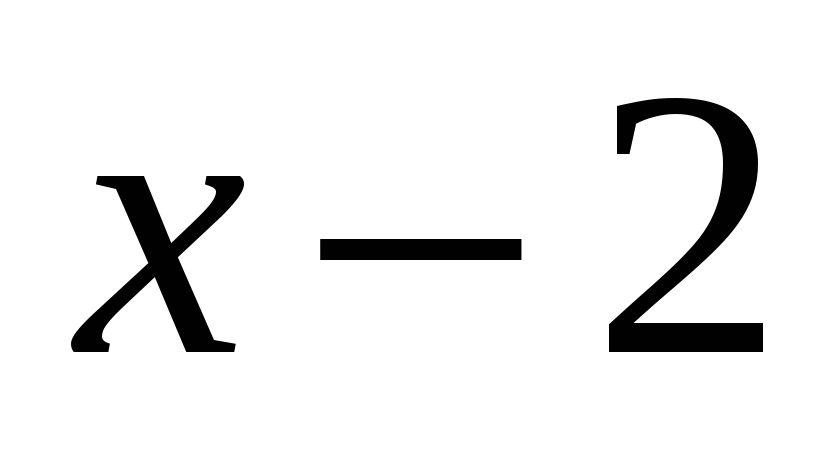és
pozitívak és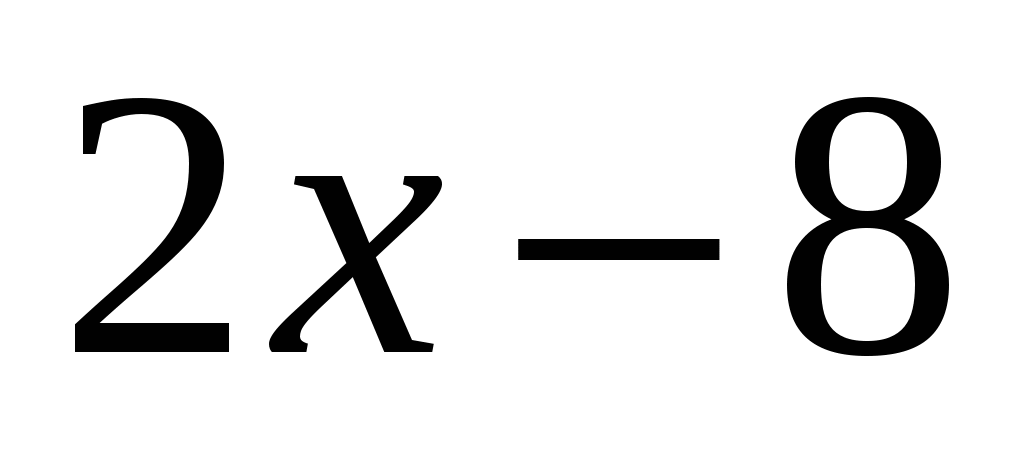
- negatívan. A következő egyenletet kapjuk: .

Az átalakítás után a következőket kapjuk: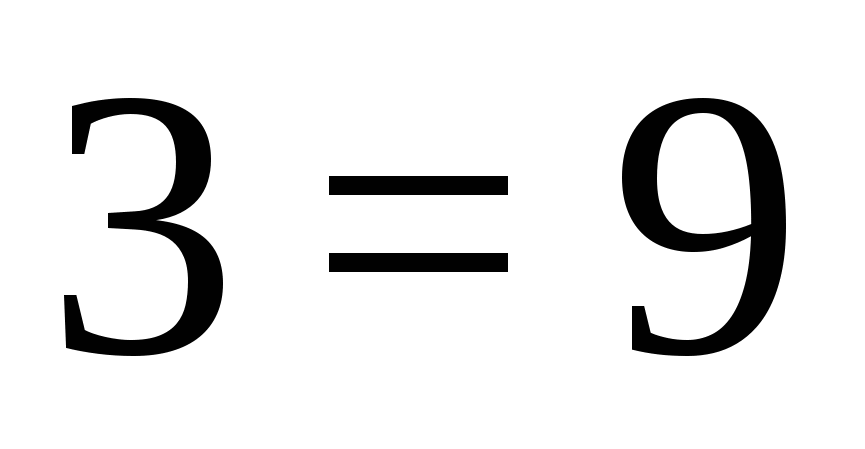
, ami azt jelenti, hogy az egyenletnek nincs gyöke ezen az intervallumon.

4) Mikor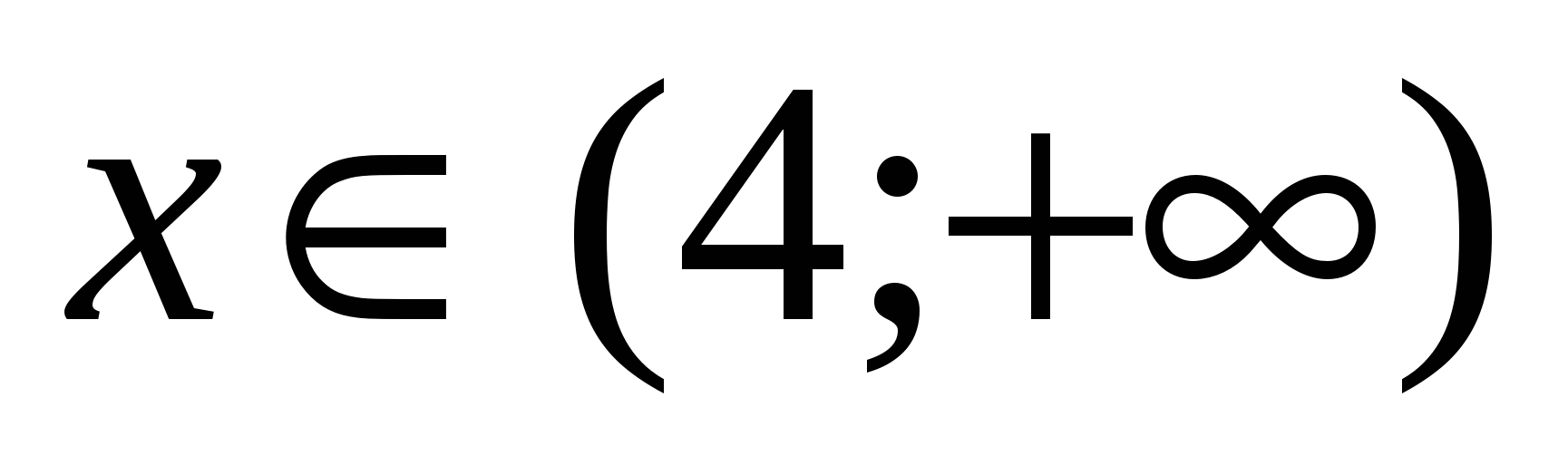
. Könnyen megállapítható, hogy ezen az intervallumon minden kifejezés pozitív, ami azt jelenti, hogy megkapjuk az egyenletet:
,
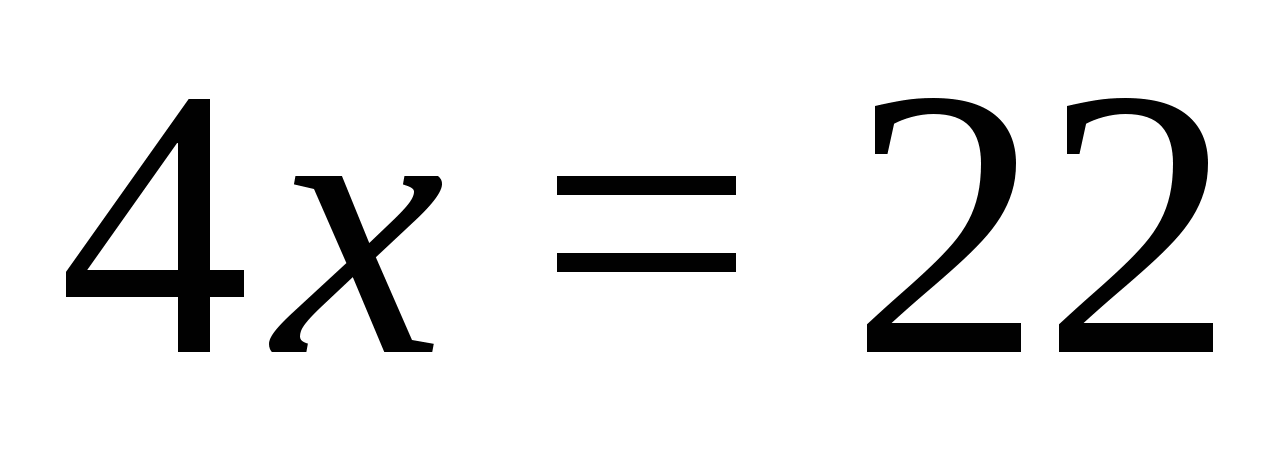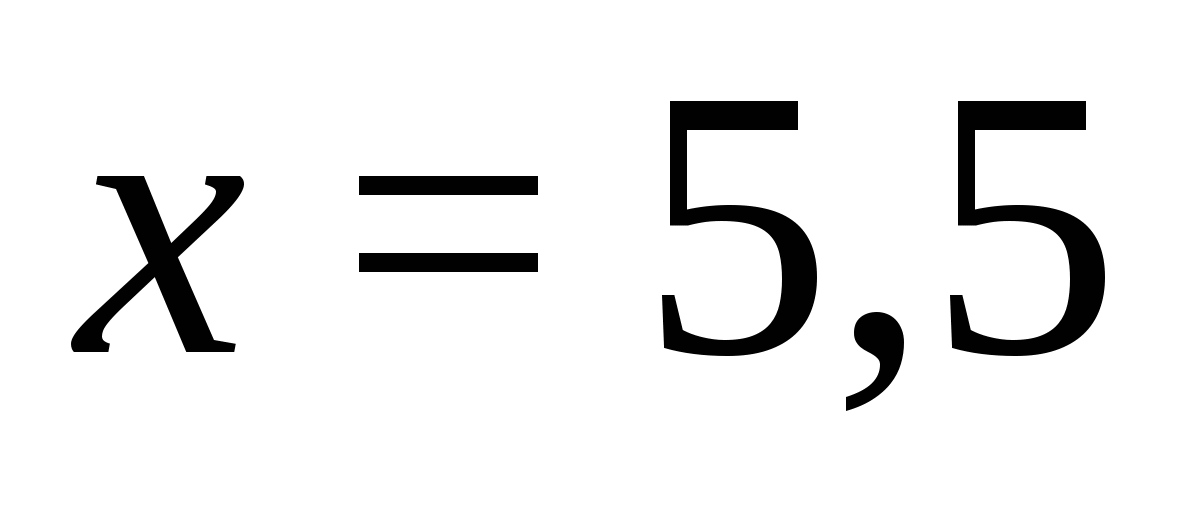amely benne van az intervallumban és az egyenlet gyöke.

Válasz.
,
.

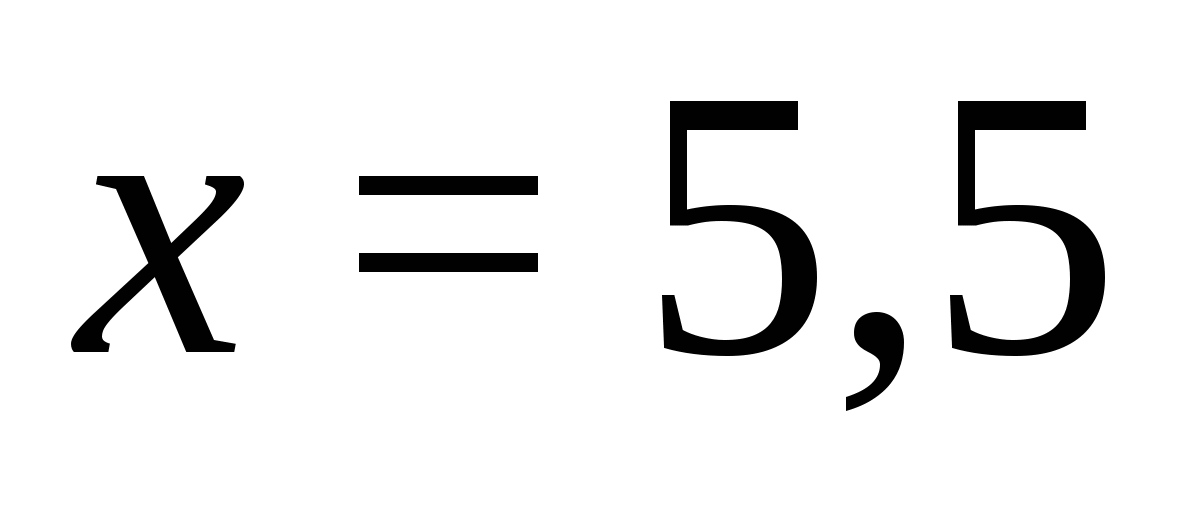• Nemnegatív kifejezések moduljait tartalmazó egyenletek megoldása

11. példa Mennyi az egyenlet gyökeinek összege (a gyökér, ha az egy)

Megoldás. Fontolja meg a kifejezést

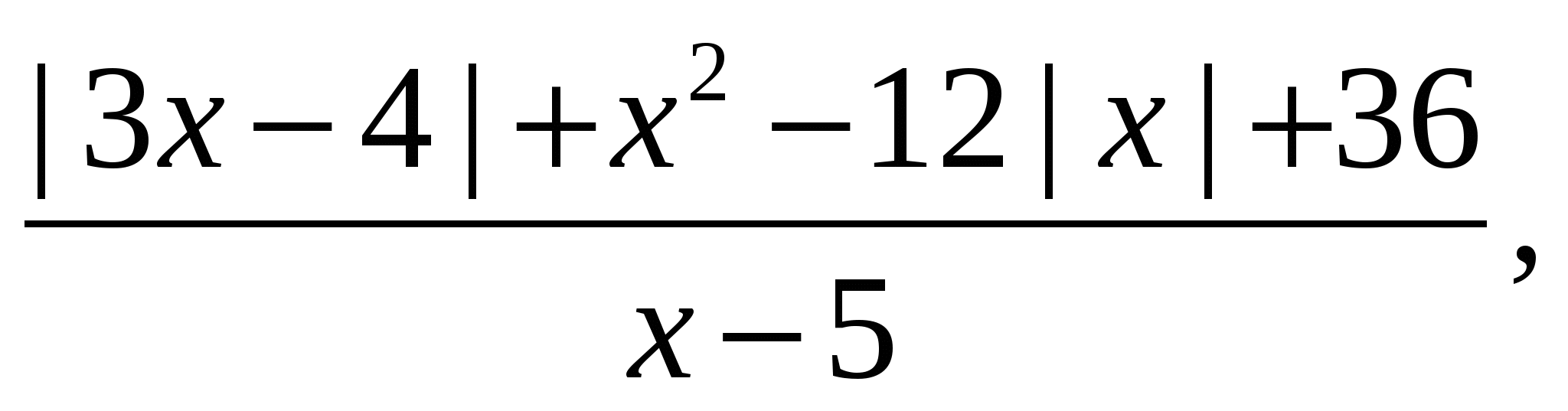és alakítsa át formára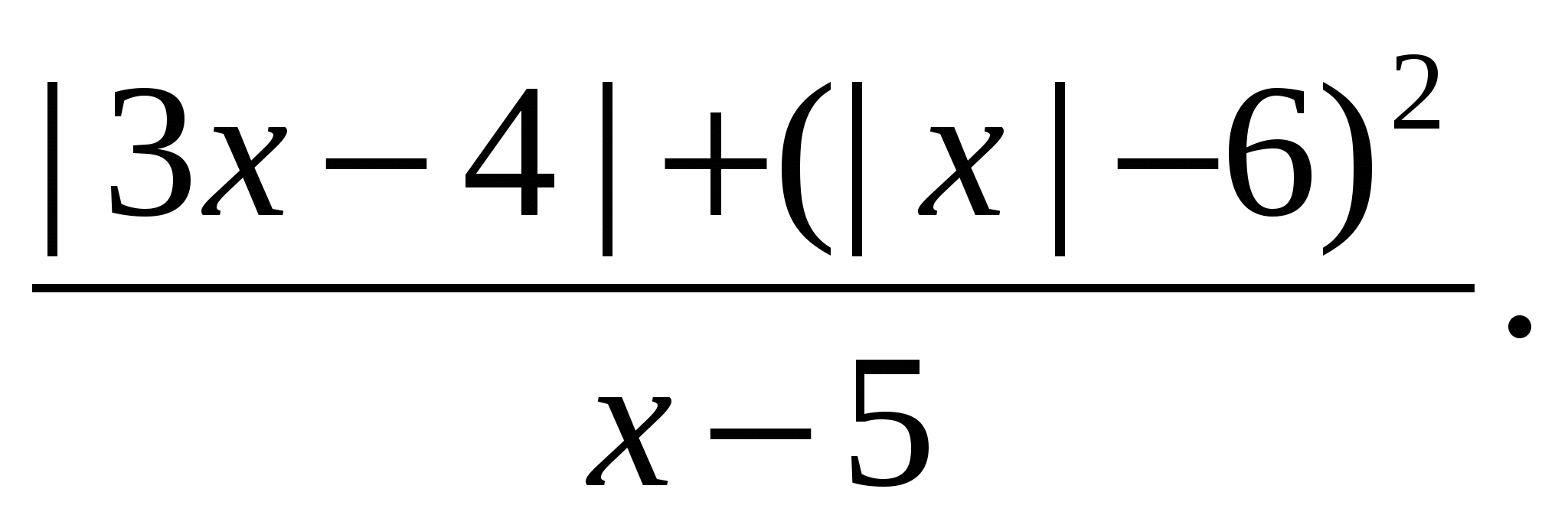

Nyilvánvaló, hogy a változó bármely értékénél a tört számlálója pozitív szám. Tehát a törtkifejezés pozitív, ha
(mivel
). A kapott kifejezést átalakítjuk, feltéve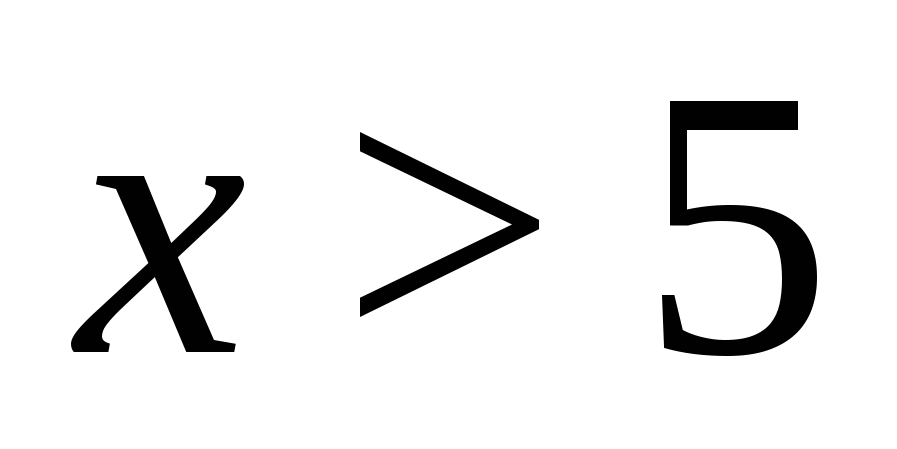
. Az eredetivel egyenértékű egyenletet kapunk:

Válasz.
.

12. példa oldja meg az egyenletet

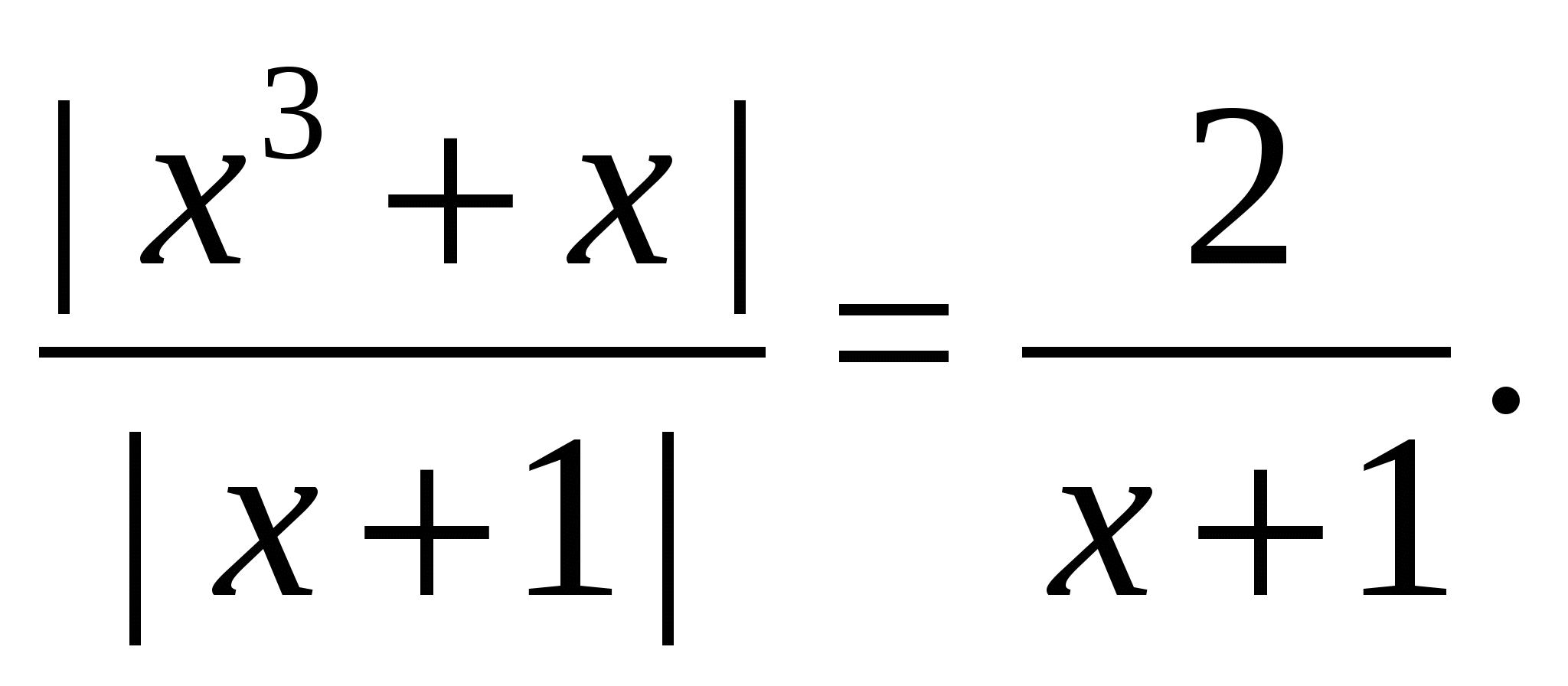
Megoldás. Mivel az egyenlet bal oldala nem negatív, a változó minden megengedett értékénél az egyenlet gyökhalmazán a jobb oldalának is nem negatívnak kell lennie, ezért a feltétel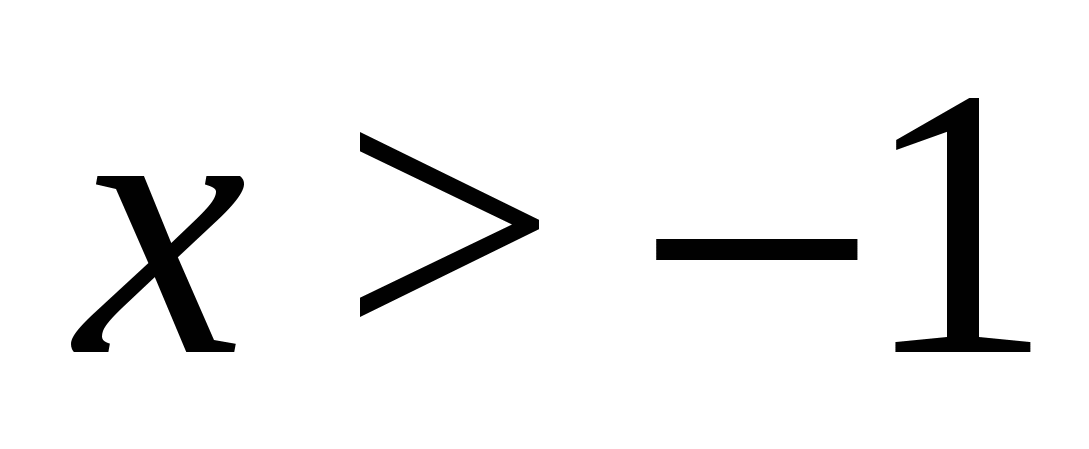
, ezen az intervallumon mindkét tört nevezője egyenlő, és hátra van az egyenlet megoldása
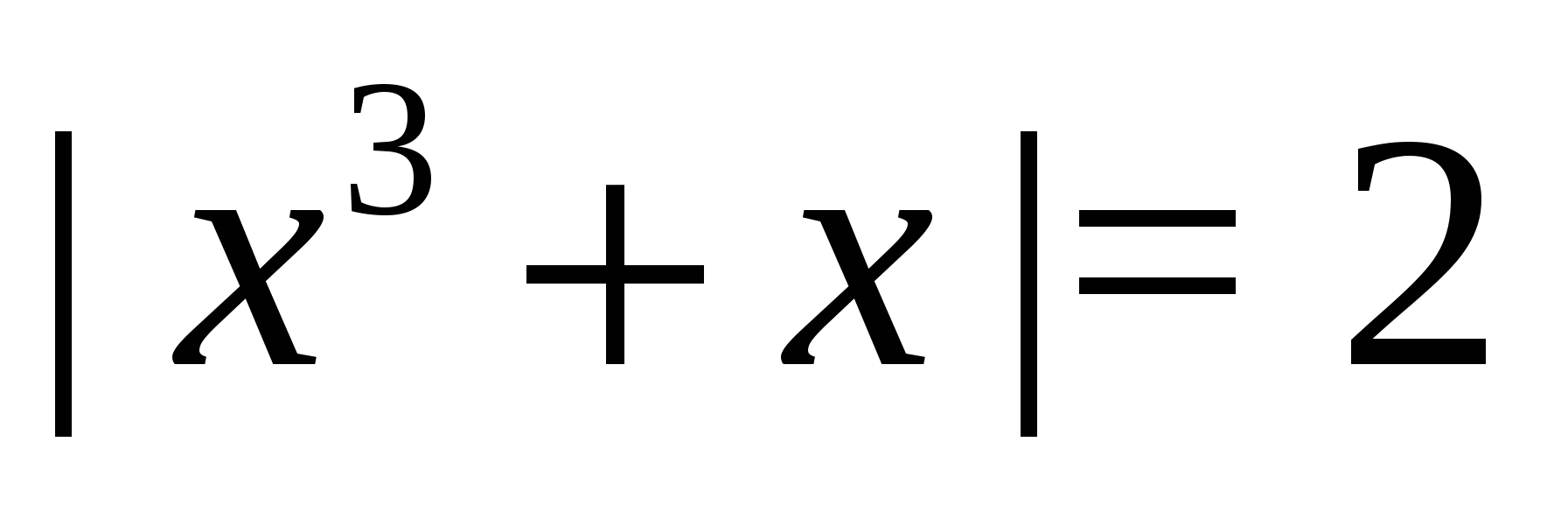. Megoldása és a korlát figyelembe vétele
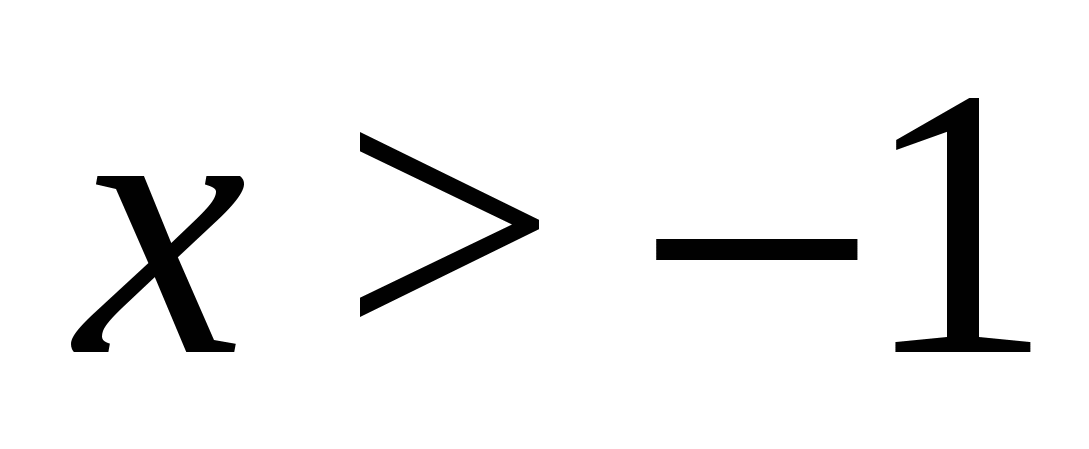, kapunk

Válasz.
.

• Egyenletek megoldása geometriai értelmezés segítségével

A kifejezés geometriai jelentése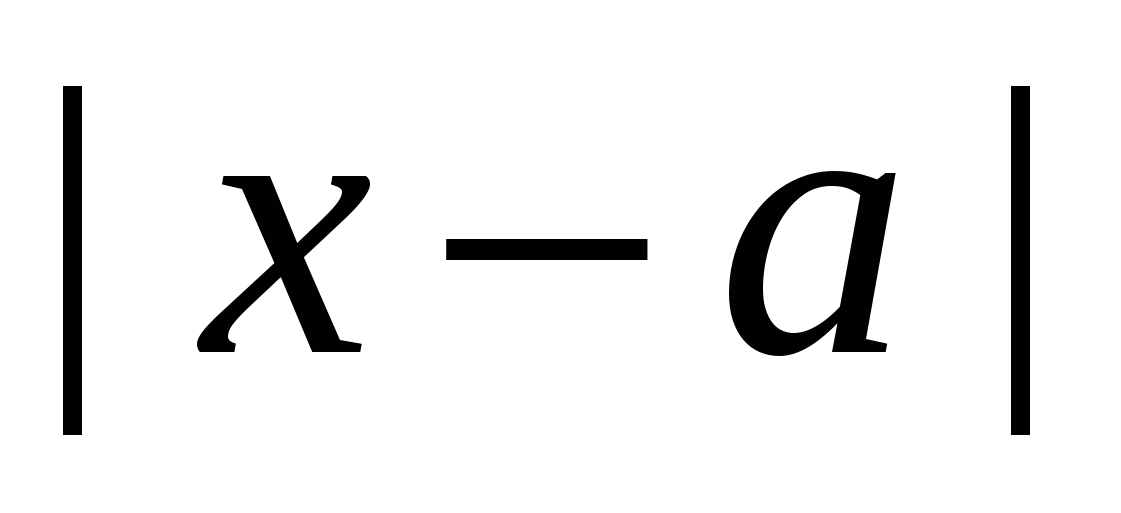
- a pontokat abszcisszákkal összekötő koordinátatengely szakaszának hossza és . Egy algebrai feladat geometriai nyelvre fordítása gyakran lehetővé teszi a nehézkes számítások elkerülését.

13. példa Oldjuk meg az egyenletet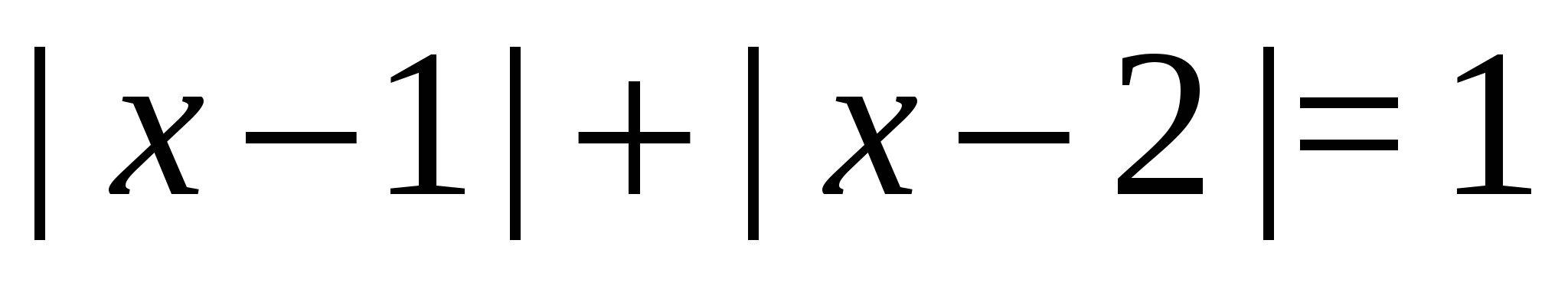
.

Megoldás. A következőképpen érvelünk: a modulus geometriai értelmezése alapján az egyenlet bal oldala az abszcissza valamely ponttól való távolságának összege. legfeljebb két fix pont az 1. és 2. abszcisszákkal. Ezután minden pont abszcisszákkal a szakaszból
rendelkezik a szükséges tulajdonsággal, míg a szegmensen kívüli pontok nem.

Válasz.
.

14. példa Oldja meg az egyenlőtlenséget
.

Megoldás. Rajzoljon pontokat a koordináta egyenesre, a távolságok összegét, amelyektől a pontokig
és pontosan egyenlő . Ezek mind határpontok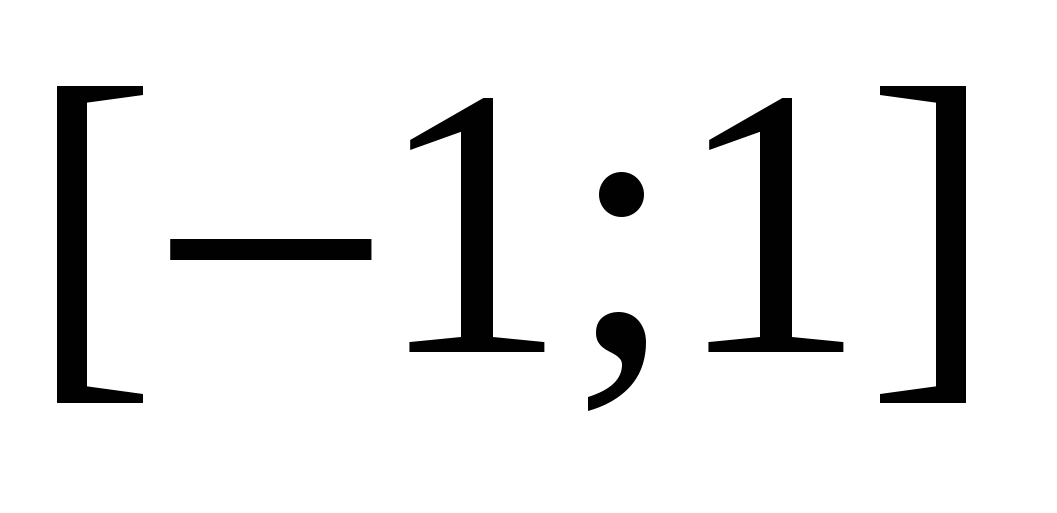
. A szegmensen kívüli összes szám esetében a távolságok összege nagyobb lesz kettőnél.

Válasz.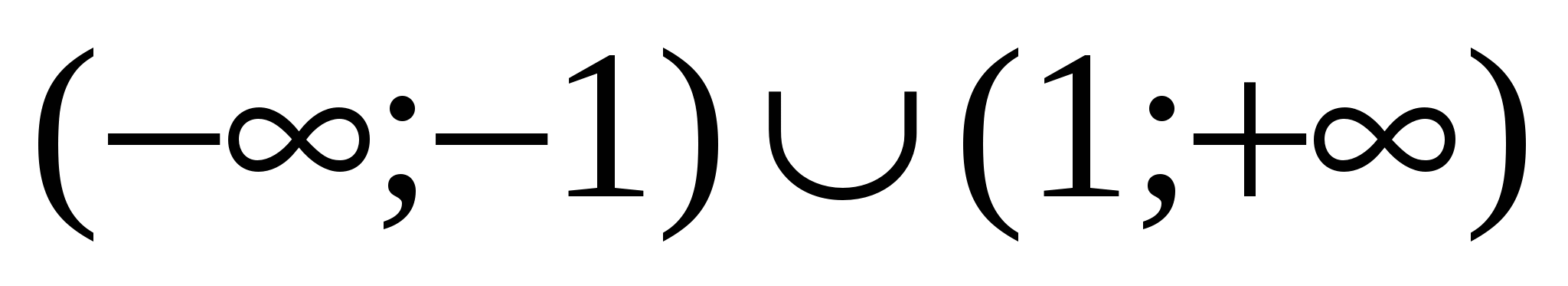
.

Példa(C3, USE – 2010) 15 oldja meg az egyenletet

Megoldás. Az identitás kétszeri alkalmazása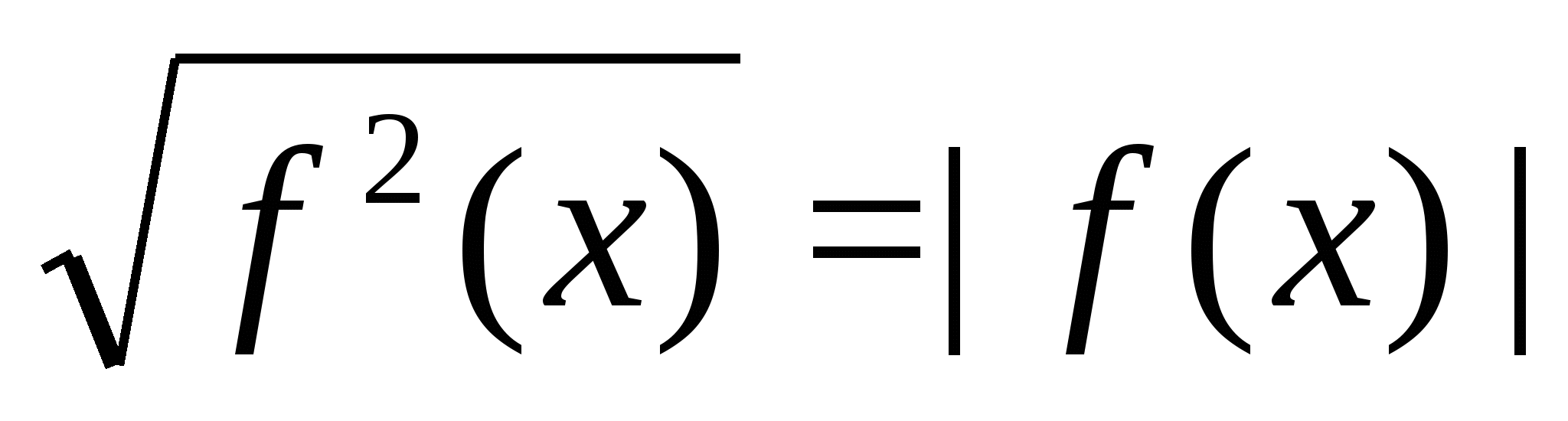
, megkapjuk az egyenletet

amelynek megoldása az intervallum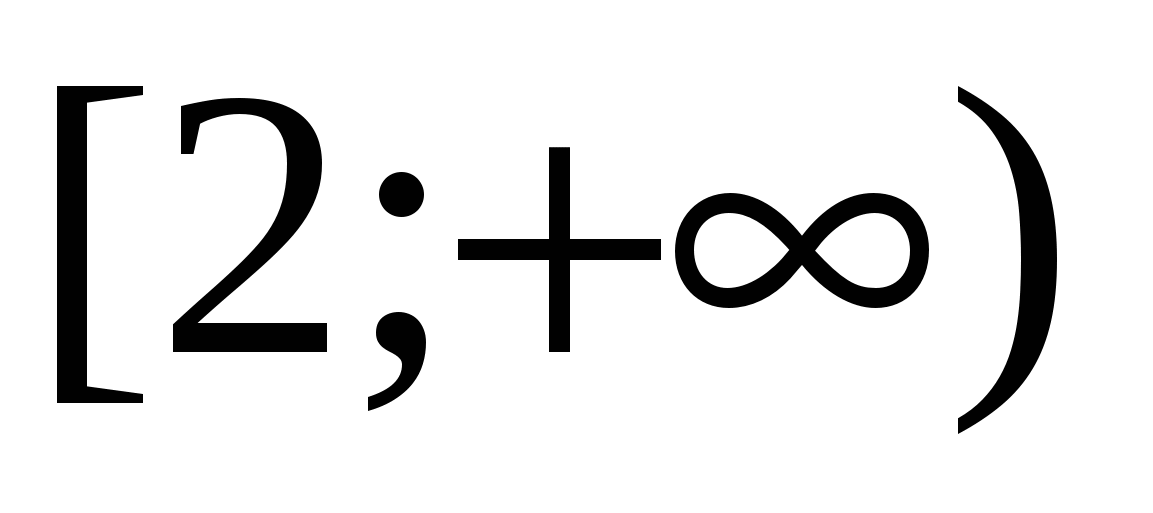
.

Válasz.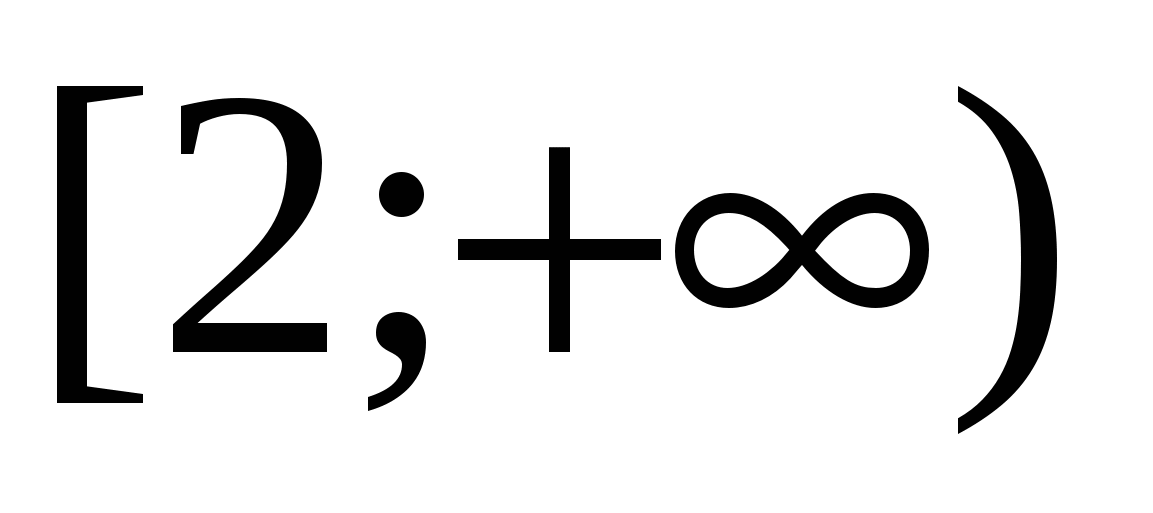
.

Példa(C3, USE – 2011) 16 17 oldja meg az egyenletet

Megoldás. .

Válasz.
.

• Az előjeltétel alkalmazása egyenletek megoldására

A szorzatokra vagy a modulusok részleges különbségeire vonatkozó egyenlőtlenségek megoldására alkalmas tételt fogalmazunk meg:

18. tétel Két kifejezés moduljai közötti különbség előjele egybeesik e kifejezések négyzeteinek különbségének előjelével. nem tűnik el a változó egyetlen értékénél sem. Ez azt jelenti, hogy a függvény a teljes definíciós tartományban állandó előjelű. Kiszámolva pl.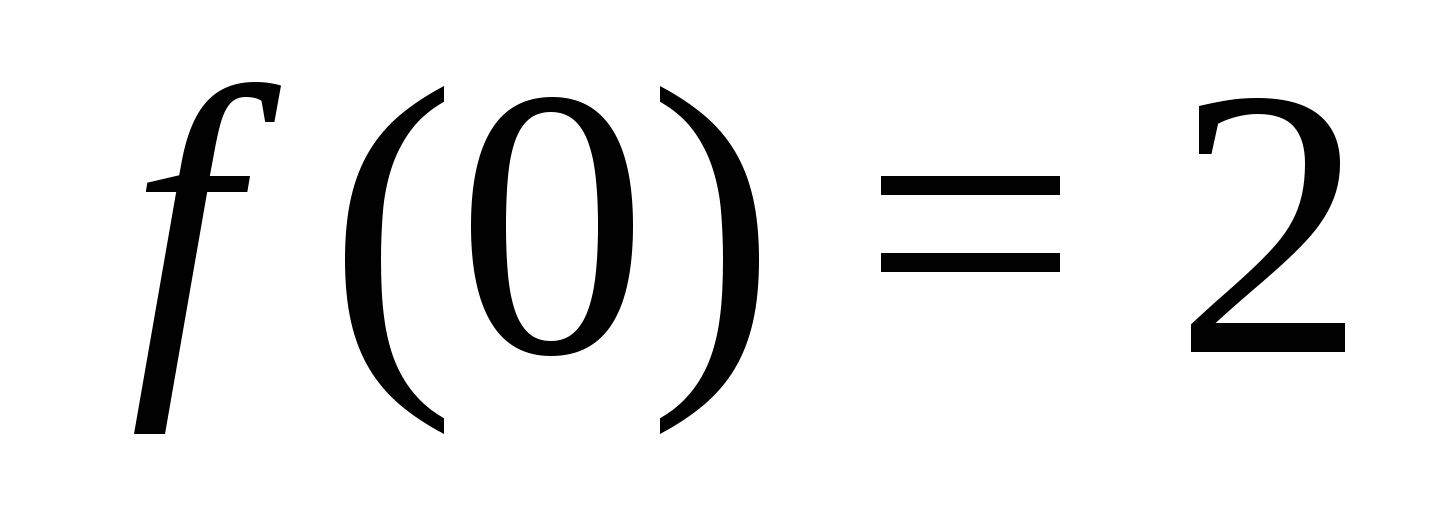
, azt kapjuk, hogy a függvény csak pozitív értékeket vesz fel.

Válasz.
.

Az intervallummódszer lehetővé teszi bonyolultabb egyenletek és egyenlőtlenségek modulokkal történő megoldását is, de ebben az esetben kicsit más a célja. A lényeg a következő. Megtaláljuk az összes szubmoduláris kifejezés gyökerét, és a numerikus tengelyt felosztjuk e kifejezések előjelállandóságának intervallumaira. Ez lehetővé teszi, hogy ezeken az intervallumokon szekvenciálisan végighaladva egyszerre megszabaduljunk minden modultól és megoldjuk a szokásos egyenletet vagy egyenlőtlenséget (miközben ellenőrizzük, hogy a talált válasz benne van-e az adott intervallumban).

• Egyenletek megoldása pozitív tényezővel való szorzással

Következtetés.

Munkánkat összegezve a következőket mondhatjuk.

A munka célja az egyenletek és egyenlőtlenségek modulokkal történő megoldásának különböző módszereinek tanulmányozása volt.

Figyelembe veszik a legegyszerűbb egyenletek és modulusos egyenlőtlenségek néhány változatát, amelyek ekvivalens átmenetek segítségével megoldhatók, valamint a modulusok összegére vonatkozó tételeket; az egyenletek grafikus megoldása. El kell mondanunk, hogy az iskolai matematika szakon ezek a megoldási módszerek a leggyakrabban használatosak. A grafikus módszer különösen fontos feladatmegoldásban C 5 a vizsga ellenőrző és mérőanyagaiból.

Ezt követően több példán keresztül más módszereket is tanulmányoztunk az egyenletek és egyenlőtlenségek modulokkal történő megoldására, nevezetesen: a modulok bővítésének módszerét; nemnegatív kifejezések moduljait tartalmazó egyenletek megoldása; egyenletek megoldása geometriai értelmezés segítségével; az identitás felhasználásával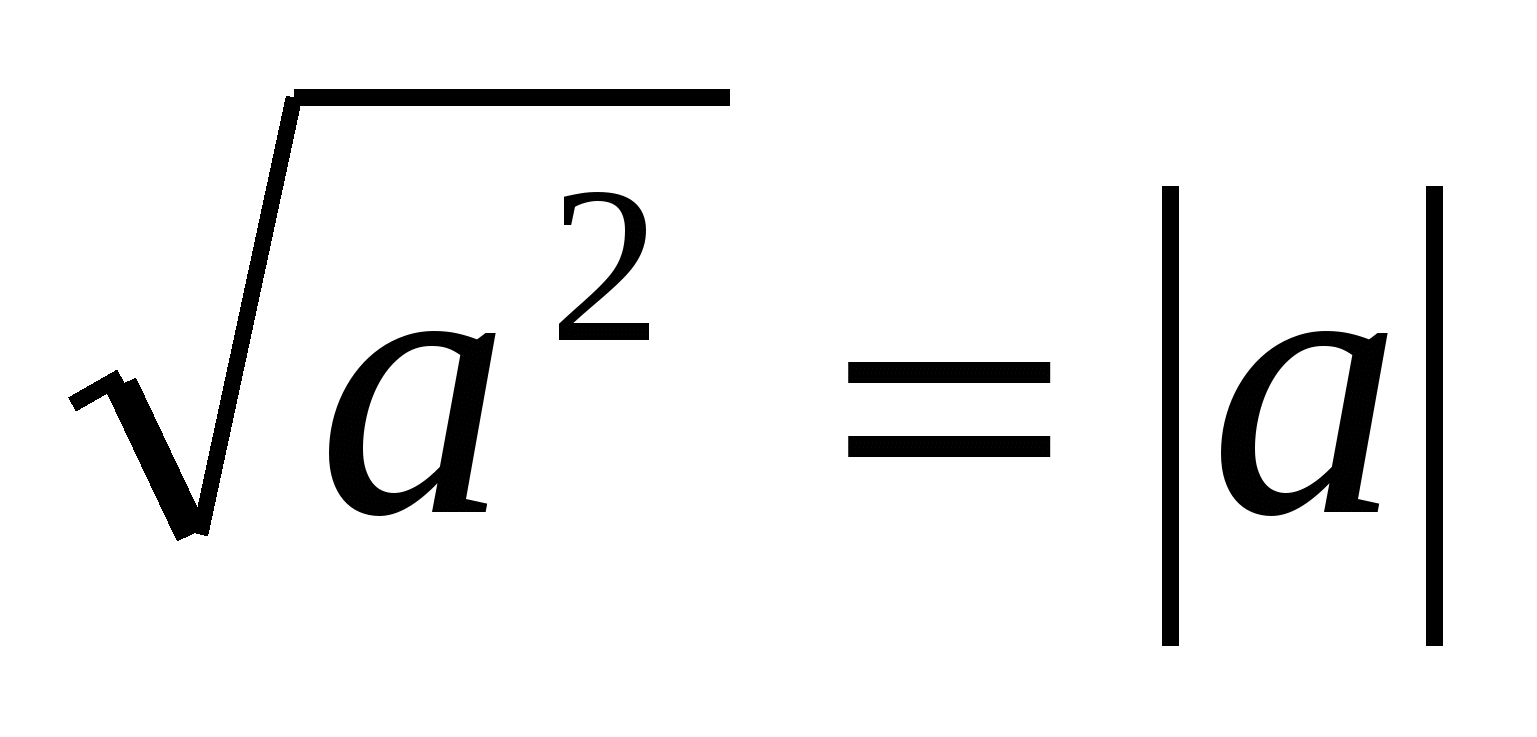
; az előjeltétel alkalmazása; egyenletek megoldása a következményre átlépve, pozitív tényezővel szorozva, valamint egyenlőtlenségek megoldása intervallum módszerrel.

Így a vizsgálat során a következő következtetésekre jutottunk.

A modulbővítési módszert, a grafikus módszert és az intervallummódszert tartjuk a leguniverzálisabbnak és a legtöbb feladatra alkalmazhatónak. Ez a meggyőződés az Egységes Államvizsga tesztanyagaiból, a tantárgyi bajnokságokból, az olimpiai feladatokból készült nagyszámú feladat megoldása, valamint a témával kapcsolatos szakirodalom tanulmányozása eredményeként született meg. Nagyon fontosnak tartjuk az identitás megismerését és alkalmazását is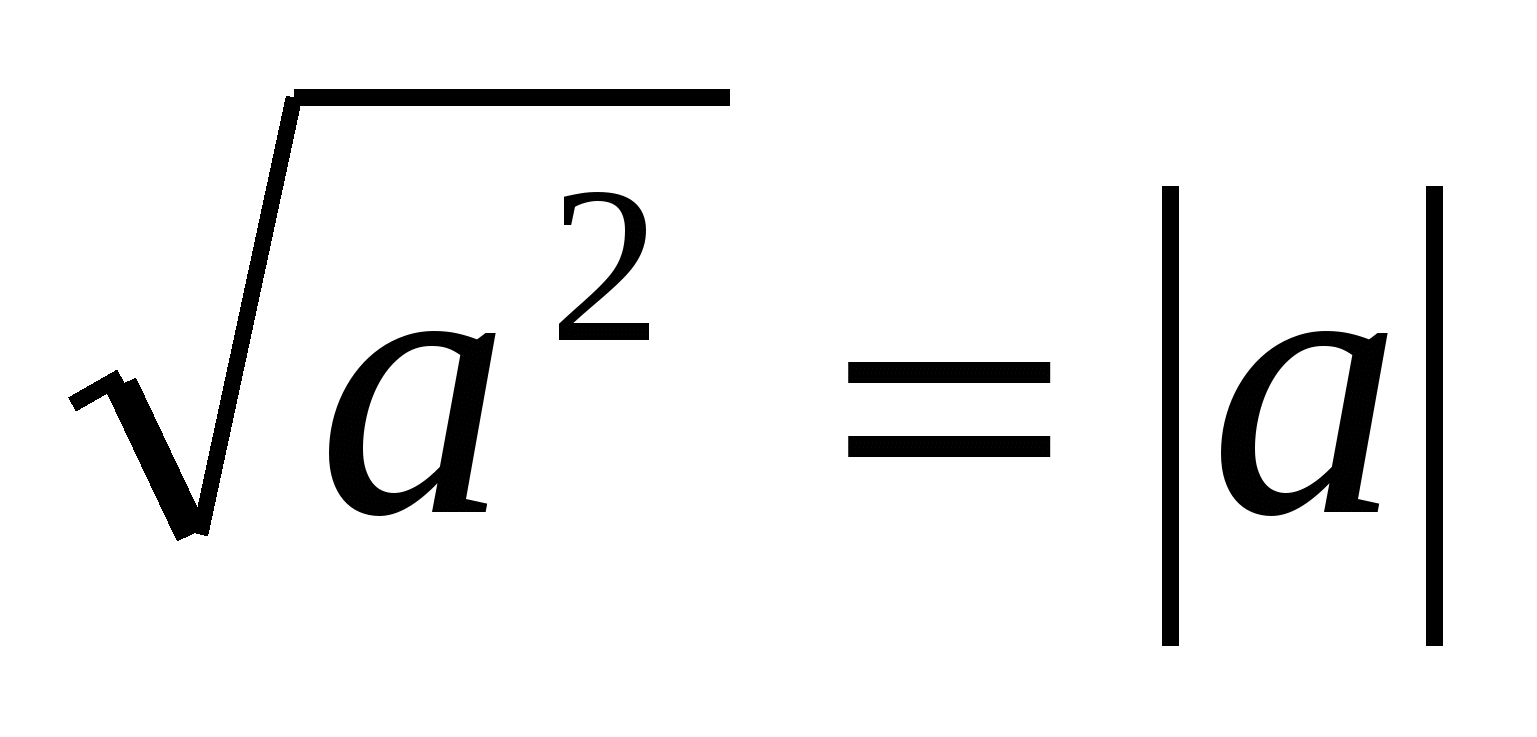
, hiszen nem csak egyenletek és egyenlőtlenségek megoldására használják, hanem számos kifejezés gyökökkel való átalakítására is. Az általunk vizsgált többi megoldási mód természetesen nagy érdeklődésre tart számot a matematikai horizont bővítése és az általános matematikai fejlődés szempontjából. Ezért tervezzük ezek felhasználását az egységes államvizsga és a felsőoktatási intézményi tanulmányokra való felkészítés formájában az állami záróbizonyítványra való felkészülésre.

Bibliográfia.

"Nagy matematikai enciklopédia" iskolásoknak és diákoknak;

Matematika. HASZNÁLAT - 2011, 2012. Standard vizsgalehetőségek. / Szerk.: A.L. Semenova, I.V. Jascsenko.

M.Ya. Vigodszkij. Az elemi matematika kézikönyve

"A legújabb tanulói kézikönyv";

Enciklopédia „Ismerem a világot. Matematika";

;